CorrelationFunction

CorrelationFunction[data,hspec]

估计数据 data 在滞后 hspec 处的相关函数.

CorrelationFunction[proc,hspec]

表示随机过程 proc 在滞后 hspec 处的相关函数.

CorrelationFunction[proc,s,t]

表示随机过程 proc 在时刻 s 和 t 的相关函数.

更多信息

  • CorrelationFunction 也被称为自相关或互相关函数（ACF 或 CCF）.
  • 可以给予 hspec 以下规范：
  • τ在时刻或滞后 τ
    {τmax}单位间隔从0到τmax
    {τmin,τmax}单位间隔从 τmin 到 τmax
    {τmin,τmax,dτ}从 τmin 到 τmax，步长为 dτ
    {{τ1,τ2,…}}使用显式的 {τ1,τ2,…}
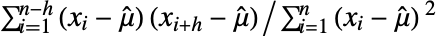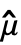  • CorrelationFunction[{x1,…,xn},h] 等价于 ，其中 =Mean[{x1,…,xn}].
  • 当 data 是包含一组路径的 TemporalData 时，输出表示在所有路径上的平均值.
  • 过程 proc 的 CorrelationFunction 是 CovarianceFunction c，由标准偏差函数 σ 的外积在时刻 s 和 t 进行正态化：
  • c[s,t]/(σ[s]σ[t])对于标量值数据或过程
    c[s,t]/(σ[s] ⊗ σ[t])对于向量值数据或过程
  • 符号 ⊗ 表示 KroneckerProduct.
  • CorrelationFunction[proc,h] 仅当 proc 是一个弱平稳过程的时候有定义，且等价于 CorrelationFunction[proc,h,0].
  • 过程 proc 可以是诸如 ARMAProcess 或 WienerProcess 的任意随机过程.

范例

打开所有单元关闭所有单元

基本范例  (4)

估计在滞后2处的相关函数：

自回归时间序列随机样本的样本相关函数：

离散时间过程的相关函数：

连续时间过程的相关函数：

范围  (13)

经验估计  (7)

估计某些数据在滞后9处的相关函数：

获取在滞后9以内的相关函数的经验估计：

计算步长为2、滞后从1到9的相关函数：

计算时间序列的相关函数：

多个滞后时间序列的相关函数由时间序列给出：

估计一组路径的相关函数：

比较经验和理论相关函数：

绘制向量数据的互相关：

随机过程  (6)

一个弱平稳离散时间过程的相关函数：

相关函数只取决于反对角线 ：

一个弱平稳连续时间过程的相关函数：

相关函数只取决于反对角线 ：

一个非弱平稳离散时间过程的相关函数：

相关函数与两个时间参数均有关：

一个非弱平稳连续时间过程的相关函数：

相关函数与两个时间参数均有关：

一些时间序列过程的相关函数：

向量 ARProcess 的互相关图形：

应用  (2)

确定下列数据是用 MAProcess 模拟还是用 ARProcess 模拟效果最好：

很难从样本路径确定底层过程：

数据的相关性函数缓慢衰减：

显然，ARProcess 是一个比 MAProcess 更好的候选模型：

建立白噪声置信带的 ACF 图：

在95％的白噪声置信区间上绘制滞后0到20的相关：

比较不相关的白噪声：

属性和关系  (12)

样本相关函数是过程相关函数的有偏估计量：

计算样本相关性函数：

过程的相关函数：

绘制两个函数：

过程的相关函数是 Correlation 矩阵的非对角线项：

滞后0的样本相关始终为1：

样本相关函数与 CovarianceFunction 相关：

经缩放的样本协方差函数：

样本相关函数与 AbsoluteCorrelationFunction 相关：

按第一个元素进行缩放：

与样本相关函数比较：

使用 Expectation 计算相关：

定义均值和标准差函数：

相同时间的相关函数减少为1：

相关函数 与 CovarianceFunction 有关：

对于 ，标准差函数为 ：

相关函数与 Correlation 有关：

这是协方差矩阵的非对角项：

相关函数对于 ToInvertibleTimeSeries 是不变的：

相关函数对于集中化是不变的：

数据的均值非零：

集中化数据：

比较相关函数：

样本相关函数之和是一个常数：

样本是随机的：

计算从 1 到 n-1 的样本相关函数：

计算和：

可能存在的问题  (1)

CorrelationFunction 的输出可能包含 DifferenceRoot：

使用 FunctionExpand 来恢复显式的幂：

Wolfram Research (2012)，CorrelationFunction，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CorrelationFunction.html.

文本

Wolfram Research (2012)，CorrelationFunction，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CorrelationFunction.html.

CMS

Wolfram 语言. 2012. "CorrelationFunction." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/CorrelationFunction.html.

APA

Wolfram 语言. (2012). CorrelationFunction. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CorrelationFunction.html 年

BibTeX

@misc{reference.wolfram_2024_correlationfunction, author="Wolfram Research", title="{CorrelationFunction}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CorrelationFunction.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_correlationfunction, organization={Wolfram Research}, title={CorrelationFunction}, year={2012}, url={https://reference.wolfram.com/language/ref/CorrelationFunction.html}, note=[Accessed: 21-November-2024 ]}