CramerVonMisesTest

CramerVonMisesTest[data]

Cramér–von Mises検定を使い，data が正規分布に従っているかどうかを調べる．

CramerVonMisesTest[data,dist]

Cramér–von Mises検定を使い，data が dist に従った分布かどうかを調べる．

CramerVonMisesTest[data,dist,"property"]

"property"の値を返す．

詳細とオプション

  • CramerVonMisesTestは data が分布 dist に従う母集団から取られたという帰無仮説 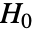とそうではないという対立仮説 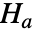でCramér–von Misesの適合度検定を行う．
  • デフォルトで，確率値つまり 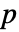値が返される．
  • 小さい 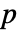値は data が dist から来ている可能性が低いことを示す．
  • dist は，記号および数値の母数，またはデータ集合，を持つ任意の記号分布でよい．
  • data は一変量{x1,x2,…}でも多変量{{x1,y1,…},{x2,y2,…},…}でもよい．
  • Cramér–von Mises検定はデータが連続分布のものであると仮定する．
  • Cramér–von Mises検定は事実上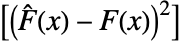の予測値に基づく検定統計を使う．ただし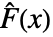，は data の経験的累積分布関数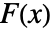，は dist の累積分布関数である．
  • 一変量データについては，検定統計は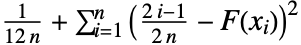で与えられる．
  • 多変量検定では一変量限界 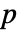値の総和が使われる．総和は 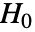のもとでUniformSumDistributionに従うものと想定される．
  • CramerVonMisesTest[data,dist,"HypothesisTestData"]は，HypothesisTestDataオブジェクト htd を返す．これは htd["property"]として追加的な検定結果と特性の抽出に使うことができる．
  • CramerVonMisesTest[data,dist,"property"]を使って直接"property"の値を与えることができる．
  • 検定結果のレポートに関連する特性
  • "PValue" 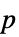値
    "PValueTable""PValue"のフォーマットされたバージョン
    "ShortTestConclusion"検定結果の簡単な説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計と 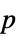値
    "TestDataTable""TestData"のフォーマットされたバージョン
    "TestStatistic"検定統計
    "TestStatisticTable""TestStatistic"のフォーマットされたバージョン
  • 次の特性はどの検定が行われているかに依存しない．
  • データ分布に関連する特性
  • "FittedDistribution"データのフィットした分布
    "FittedDistributionParameters"データの分布母数
  • 使用可能なオプション
  • Method Automatic 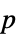値を計算するメソッド
    SignificanceLevel0.05診断とレポートのための切捨て
  • 適合度検定では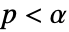， のときにのみ 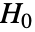が棄却されるような切捨て 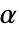が選択される．特性"TestConclusion"および"ShortTestConclusion"で使われる 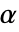の値はSignificanceLevelオプションで制御される．デフォルトで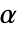， は0.05に設定されている．
  • Method->"MonteCarlo"の設定では，入力 si と同じ長さの 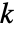個のデータ集合が，フィットされた分布を使って 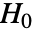のもとで生成される．次に，CramerVonMisesTest[si,dist,"TestStatistic"]からの経験分布を使って 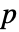値が推定される．

例題

すべて開くすべて閉じる

例  (3)

正規性についてCramér–von Mises検定を行う：

QuantilePlotを使って結果を検証する：

あるデータが特定の分布にフィットするかどうかの検定を行う：

2つのデータ集合の分布を比較する：

スコープ  (9)

検定  (6)

正規性についてCramér–von Mises検定を行う：

正規データの 値は，非正規データの 値と比べて大きい：

特定の分布に対して適合度検定を行う：

2つのデータ集合の分布を比べる：

2つのデータ集合は同じ分布に従わない：

多変量正規性について検定する：

任意多変量分布について適合度検定を行う：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

抽出に使用できる特性：

レポート  (3)

Cramér–von Mises検定の結果を表にする：

完全な検定表：

値の表：

検定統計：

カスタマイズされたレポート用にCramér–von Mises検定表から項目を取り出す：

"ShortTestConclusion"と"TestConclusion"を使って検定の結論をレポートする：

有意水準が異なると，結論も異なることがある：

オプション  (3)

Method  (3)

モンテカルロ(Monte Carlo)法に基づくメソッドまたは計算式を使う：

モンテカルロ法に基づくメソッドで使うサンプル数を設定する：

モンテカルロ推定は，サンプルを増やすと，真の 値に収束する：

モンテカルロ法に基づくメソッドで使われるランダムなシードを設定する：

シードは生成器の状態に影響を与え，結果の 値にもいくらか影響を与える：

アプリケーション  (3)

Cramér–von Mises検定の検出力曲線：

近似検出力曲線を可視化する：

基礎となる分布がUniformDistribution[{-4,4}]であり，検定サイズが0.05，サンプルサイズが32である場合に，Cramér–von Mises検定の検出力を推定する：

同次ポワソン(Poisson)過程によって生成される観察は，完全な空間ランダム性を示すはずである．これは，観察が同一分布から導き出されたことを示唆する．以下の画像からの観察が均質ポワソン過程でうまくモデル化できるかどうかを見極める：

各点の中心を求め，について再スケールする：

最初の画像の点は，均質ポワソン過程でうまくモデル化できる：

2つ目のグループのモデルは，依存性を説明しなければならない：

Cramér–von Mises検定統計を最小化する分布の母数を求める：

結果をFindDistributionParametersと比べる：

特性と関係  (8)

デフォルトで一変量データはNormalDistributionと比べられる：

母数はデータから推定されている：

多変量データは，デフォルトでMultinormalDistributionと比べられる：

検定分布の母数は，指定されない場合にはデータから推測される：

指定された母数は推測されない：

最尤推定値は，検定分布の指定されていない母数に使われる：

母数が未知の場合，CramerVonMisesTestは可能であれば修正を適用する：

母数は推定されるが，修正は適用されない：

フィットされた分布は前と同じであり， 値は修正される：

独立周辺密度が多変量の適合度検定では仮定される：

独立性が仮定されると，検定統計は同一である：

Cramér–von Mises検定はNExpectationを使って定義することができる：

Cramér–von Mises検定は，入力がTimeSeriesのときにのみ値に使うことができる：

考えられる問題  (3)

Cramér–von Mises検定は離散分布には使えない：

一般に連続性の訂正は検定サイズの保全の点からするとうまくいく：

しかし場合によってはこれが当て嵌まらないこともある：

そのような場合にはモンテカルロ法またはPearsonChiSquareTestを使う：

母数がデータから推定される場合には，Cramér–von Mises検定は，分布によっては有効ではないことがある：

母数の値が既知である場合には与える：

あるいは，モンテカルロ法を使って 値を近似する：

Cramér–von Mises検定のサンプルサイズは，有効な 値を得るためには少なくとも7でなければならない：

モンテカルロ法を使って有効な 値に辿り着く：

おもしろい例題  (1)

帰無仮説 が真であるときの統計量を計算する：

特定の対立仮説によって与えられた検定統計：

検定統計の分布を比較する：

Wolfram Research (2010), CramerVonMisesTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/CramerVonMisesTest.html.

テキスト

Wolfram Research (2010), CramerVonMisesTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/CramerVonMisesTest.html.

CMS

Wolfram Language. 2010. "CramerVonMisesTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CramerVonMisesTest.html.

APA

Wolfram Language. (2010). CramerVonMisesTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CramerVonMisesTest.html

BibTeX

@misc{reference.wolfram_2024_cramervonmisestest, author="Wolfram Research", title="{CramerVonMisesTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/CramerVonMisesTest.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_cramervonmisestest, organization={Wolfram Research}, title={CramerVonMisesTest}, year={2010}, url={https://reference.wolfram.com/language/ref/CramerVonMisesTest.html}, note=[Accessed: 21-November-2024 ]}