Cumulant

Cumulant[data,r]

data の r 次キュムラントを与える．

Cumulant[data,{r₁,…,r_m} ]

data の{r₁,…,r_m}次多変量キュムラントを与える．

Cumulant[,r]

分布 dist の r 次キュムラントを与える．

Cumulant[r]

r 次の形式的なキュムラントを表す．

詳細

r 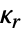次キュムラント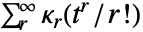は，形式的にはCumulantGeneratingFunctionのテイラー(Taylor)級数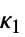の係数として定義される．
次は，モーメントによって表現される最初のいくつかのキュムラントである．
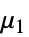
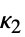
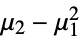
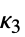
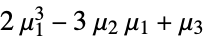
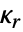
一般に，MomentConvert[Cumulant[r],"Moment"]はモーメントによって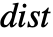を与える．
Cumulant[data,r]は，事実上，MomentConvertを使ってデータについての他のモーメントによってこれを計算する．
x∈Arrays[{n₁,n₂,… ,n_k}]のとき，Cumulant[x,r]はArrayReduce[Cumulant[#,r]&,data,1]に等しい． »
x∈Arrays[{n₁,n₂,… ,n_k}]のとき，Cumulant[x,{r₁,…,r_m}]はArrayReduce[Cumulant[#,{r₁,…,r_m}]&,x,{{1},{2}}]に等しい． »
Cumulantは，数値データと数式データの両方を扱う．
data は，以下の追加的な形式と解釈を持つことができる．

	Association	値（キーは無視される） »
	WeightedData	もとになっているEmpiricalDistributionに基づく加重平均 »
	EventData	もとになっているSurvivalDistributionに基づく »
	TimeSeries, TemporalData, …	のベクトルまたは配列（タイムスタンプは無視される） »
	Image,Image3D	RGBチャンネル値またはグレースケールの強度値 »
	Audio	すべてのチャンネルの振幅値 »
	DateObject, TimeObject	日付のリストまたは時間のリスト »

分布 dist については G=CumulantGeneratingFunction[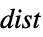,…]である．
Cumulant[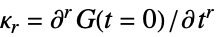,r] »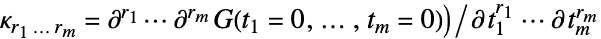

Cumulant[dist,{r₁,…,r_m}] »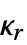
ランダム過程 proc については，キュムラント関数は時点 t におけるスライス分布SliceDistribution[proc,t]について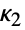，[t]=Cumulant[SliceDistribution[proc,t],r]として計算することができる． »
Cumulant[r]は，MomentConvertやMomentEvaluate等の関数で使うことができる． »

例題

すべて開くすべて閉じる

例 (3)

データからキュムラントを計算する：

記号データについて：

日付のリストのキュムラント：

一変量連続分布の二次キュムラントを計算する：

多変量分布のキュムラント：

スコープ (26)

基本的な用法 (6)

厳密な入力は厳密な出力を与える：

近似入力は近似出力を与える：

WeightedDataのキュムラントを求める：

EventDataのキュムラントを求める：

TimeSeriesのキュムラントを求める：

キュムラントは値のみに依存する：

数量を含むデータについてのキュムラントを求める：

配列データ (5)

Cumulantは，行列に対しては列ごとの平均を与える：

Cumulantは，配列に対しては第1レベルの列ごとの平均を与える：

大きい配列に使うことができる：

入力がAssociationのとき，Cumulantはその値に作用する：

SparseArrayデータは密な配列のように使うことができる：

配列の多変量キュムラントをその生のモーメントについて計算する：

画像データと音声データ (2)

RGB画像のチャンネルごとのキュムラント：

グレースケール画像のキュムラント強度値：

Cumulantは，音声オブジェクトに対してはチャンネルごとに作用する：

日付と時間 (4)

日付のキュムラントを計算する：

日付の重み付きキュムラントを計算する：

単純なキュムラントで計算する：

異なる暦で与えられた日付のキュムラントを計算する：

時間のキュムラントを計算する：

異なる時刻帯指定の時刻のリスト：

分布キュムラントと過程キュムラント (5)

一変量分布のスカラーキュムラント：

多変量分布のスカラーキュムラント：

多変量分布の結合キュムラント：

記号次数 r についてのキュムラントを計算する：

キュムラントは特定の次数についてしか評価できないことがある：

キュムラントは数値的にしか評価できないことがある：

派生分布についてのキュムラント：

データ分布について：

ランダム過程についてのキュムラント関数：

時点 t=0.5におけるTemporalDataのキュムラントを求める：

対応するキュムラント関数をすべてのシミュレーションとともに求める：

形式的なキュムラント (4)

形式的なキュムラントのTraditionalFormによる表示：

形式的なモーメントの組合せをCumulantを含む式に変換する：

分布についての形式的なキュムラントを含む式を評価する：

データについて評価する：

Cumulantを含む式についてのサンプル推定量を求める：

結果の推定量をデータについて評価する：

アプリケーション (5)

キュムラント法を使って分布母数を推定する：

大数の法則にはサンプルサイズが大きくなるにつれてサンプルモーメントは母集団のモーメントに近付くとある．Histogramを使い，さまざまなサンプルサイズについて，標準正規確率変量のサンプルキュムラントの確率分布を示す：

次数のエッジワース(Edgeworth)の展開：

SechDistributionを近似する：

あるデータについての移動キュムラントを計算する：

長さ.1の窓を使う：

ランダム過程の経路集合のスライスについてキュムラントを計算する：

いくつかの時間スライスを選ぶ：

これらの経路上でキュムラントをプロットする：

特性と関係 (5)

一次キュムラントは一次モーメントと等しい：

二次キュムラントは二次中心モーメントと等しい：

三次キュムラントは三次中心モーメントと等しい：

キュムラントはキュムラント母関数の次導関数とゼロにおいて等しい：

Cumulantを直接使う：

GeneratingFunctionを使ってキュムラント母関数を求める：

CumulantGeneratingFunctionを使って検証する：

形式的には，キュムラントはCumulantGeneratingFunction[dist,t]がLog[MomentGeneratingFunction[dist,t]]によって与えられるという事実を使って計算できる：

母関数の観点からのモーメントの定義を代入する：

データについてのCumulantのサンプル推定量は偏っている：

サイズを仮定してサンプリング母集団の期待値を求める：

PowerSymmetricPolynomialを使ってサンプルの不偏推定量を構築する：

サイズの小さいサンプルで不偏性を調べる：

サンプル推定量は偏っている：

サンプル推定量のサンプリング母集団の期待値と比較する：

考えられる問題 (1)

裾部の長い分布の中にはいくつかの次数の低いキュムラントしか定義されないものもある：

おもしろい例題 (2)

キュムラントの積について不偏推定量を求める：

サンプリング母集団の期待値をチェックする：

20個，100個，300個のサンプルについてのCumulant推定値の分布：

トップへ

その他のラーニングリソース

テクニカルサポート

Wolframソリューション

教育のためのWolframソリューション

使い始める

Grow Your Skills

Wolframと繋がる

大人用の教育プログラム

若者のための教育プログラム

読む

Cumulant

詳細

例題

例 (3)