Search for all pages containing Disk
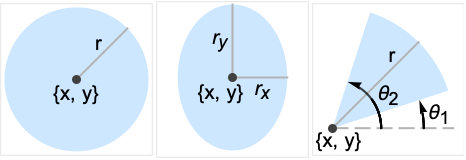
Disk[{x,y},r]
represents a disk of radius r centered at {x,y}.
Disk[{x,y}]
gives a disk of radius 1.
Disk[{x,y},{rx,ry}]
gives an axis-aligned elliptical disk with semiaxes lengths rx and ry.
Disk[{x,y},…,{θ1,θ2}]
gives a sector of a disk from angle θ1 to θ2.
Disk[{{x1,y1},{x2,y2},…},…]
gives multiple identical disks centered at the given coordinates.


Disk
Disk[{x,y},r]
represents a disk of radius r centered at {x,y}.
Disk[{x,y}]
gives a disk of radius 1.
Disk[{x,y},{rx,ry}]
gives an axis-aligned elliptical disk with semiaxes lengths rx and ry.
Disk[{x,y},…,{θ1,θ2}]
gives a sector of a disk from angle θ1 to θ2.
Disk[{{x1,y1},{x2,y2},…},…]
gives multiple identical disks centered at the given coordinates.
Details and Options

- Disk can be used as a geometric region and a graphics primitive.
- Disk[] is equivalent to Disk[{0,0}]. »
- Disk represents the filled region
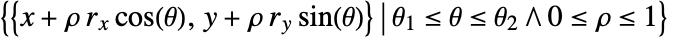 .
. - Angles are measured in radians counterclockwise from the positive x direction.
- Disk can be used in Graphics.
- In graphics, the points {xi,yi} can be Scaled, Offset, ImageScaled, and Dynamic expressions.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, and color.
- Disk can be used with symbolic points and quantities in GeometricScene.
Background & Context
- Disk is a graphics and geometry primitive that represents a circular disk, elliptical disk or sector in the plane. In particular, Disk[{x,y},r] represents the disk of radius r in
 centered at {x,y}, Disk[{x,y},{rx,ry}] represents the axis-aligned filled ellipse in
centered at {x,y}, Disk[{x,y},{rx,ry}] represents the axis-aligned filled ellipse in  with center {x,y} and semiaxis lengths rx and ry, and Disk[{x,y},…,{θ1,θ2}] represents the (potentially elliptical) sector centered at {x,y} ranging between angles θ1 and θ2 measured in radians counterclockwise from the positive
with center {x,y} and semiaxis lengths rx and ry, and Disk[{x,y},…,{θ1,θ2}] represents the (potentially elliptical) sector centered at {x,y} ranging between angles θ1 and θ2 measured in radians counterclockwise from the positive 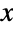 axis. The shorthand form Disk[{x,y}] is equivalent to Disk[{x,y},1], while Disk[] autoevaluates to Disk[{0,0},1].
axis. The shorthand form Disk[{x,y}] is equivalent to Disk[{x,y},1], while Disk[] autoevaluates to Disk[{0,0},1]. - Disk objects can be formatted by placing them inside a Graphics expression. The appearance of Disk objects in graphics can be modified by specifying edge and face directives EdgeForm and FaceForm, color directives such as Red, the transparency directive Opacity, and the style option Antialiasing.
- Disk may also serve as a region specification over which a computation should be performed. For example, Integrate[1,{x,y}∈Disk[{0,0},r]] and Area[Disk[{0,0},r]] both return the area
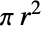 of a disk of radius
of a disk of radius 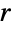 , and Perimeter[Disk[{x,y},r]] returns the perimeter
, and Perimeter[Disk[{x,y},r]] returns the perimeter 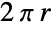 .
. - Disk is related to a number of other symbols. Circle represents the boundary of a disk, as can be computed using RegionBoundary[Disk[{x,y},r]]. Ball and Ellipsoid may be thought of as higher-dimensional analogs of disks. Annulus gives a region obtained by removing a small disk from the interior of a larger concentric disk. Disk[{x,y},r] may be alternately represented using Ball[{x,y},r], ImplicitRegion[(x-u)2+(y-v)2≤r2,{u,v}] or ParametricRegion[a{Cos[θ],Sin[θ]}-{x,y},{{θ,0,2π},{a,0,r}}]. Precomputed properties of the disk and its variants in standard position are available using LaminaData["entity","property"] or EntityValue[Entity["Lamina","entity"],"property"], where "entity" is one of "CircularSector", "Disk", "FilledEllipse", "FilledHalfEllipse", "HalfDisk", etc.
Examples
open all close allBasic Examples (5)
Differently styled unit disks:
Get the Area of a disk:
Scope (23)
Graphics (13)
Specification (7)
Styling (2)
Coordinate (4)
Use Scaled coordinates and radii:
Use ImageScaled coordinates and radii:
Use Offset coordinates:
Use Offset to specify the radii in printer's points:
Applications (11)
Use a Disk to annotate a plot of a trig function:
Archimedes' approximation of the circle area:
The hexagonal packing of disks:
Simulation of elliptical gears:
An annulus is the RegionDifference of two disks with the same center:
Maximize the area of an ellipse of fixed perimeter:
As expected, the largest such ellipse is the circular disk:
Illustrate a function's radius of curvature:
By taking a RegionUnion of many disks, dilation of a mesh can be approximated:
Create disks of the dilation radius around the mesh boundary:
Then simply take the union of all disks plus the original mesh:
By removing a RegionUnion of many disks, erosion of a mesh can be approximated:
Create disks of the erosion radius around the mesh boundary:
Then subtract the union of the disks from the original mesh:
Properties & Relations (9)
Use Rotate to get all possible elliptical disks:
The boundary of a disk defines a circle:
An implicit specification of a disk can be generated using RegionPlot:
A parametric specification of a disk can be generated using ParametricPlot:
Disk is a special case of Ball:
Disk is a special case of Ellipsoid:
ParametricRegion can represent any Disk:
ImplicitRegion can represent any Disk:
Disk is a norm ball for the Euclidean norm:
Possible Issues (2)
Using Scaled radii will depend on the PlotRange:
Using ImageScaled sizes will depend on the ImageSize and AspectRatio:
See Also
DiskSegment Circle Annulus Polygon BoundingRegion Rotate PlotRangeClipping GeometricScene
Function Repository: Disk3D
History
Introduced in 1991 (2.0) | Updated in 2014 (10.0) ▪ 2023 (13.3)
Text
Wolfram Research (1991), Disk, Wolfram Language function, https://reference.wolfram.com/language/ref/Disk.html (updated 2023).
CMS
Wolfram Language. 1991. "Disk." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/Disk.html.
APA
Wolfram Language. (1991). Disk. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Disk.html
BibTeX
@misc{reference.wolfram_2025_disk, author="Wolfram Research", title="{Disk}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/Disk.html}", note=[Accessed: 31-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_disk, organization={Wolfram Research}, title={Disk}, year={2023}, url={https://reference.wolfram.com/language/ref/Disk.html}, note=[Accessed: 31-December-2025]}