FailureDistribution
FailureDistribution[bexpr,{{x1,dist1},{x2,dist2},…}]
ブール式 bexpr がTrueであるときに頂上事象が起り xi がTrueのときに事象 xiが起ったような,信頼性分布が distiの事象 xiの系の故障分布を表す.
詳細

- FailureDistribution[bexpr,…]は故障の木の指定に対応する.
- ブール式 bexpr は系の構造関数としても知られている.
- よく使用される構造関数
-
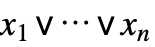
Orゲート 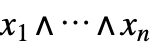
Andゲート ![TemplateBox[{BooleanCountingFunction, paclet:ref/BooleanCountingFunction}, RefLink, BaseStyle -> {2ColumnTableMod}][{k,n},n] TemplateBox[{BooleanCountingFunction, paclet:ref/BooleanCountingFunction}, RefLink, BaseStyle -> {2ColumnTableMod}][{k,n},n]](Files/FailureDistribution.ja/3.png)
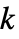 アウトオブ
アウトオブ 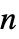 の系
の系BooleanConsecutiveFunction[k,n] 連続する 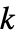 アウトオブ
アウトオブ 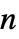 の系
の系 - 構造関数 bexpr はどの正ユネイトブール関数でもよい.
- UnateQ[bexpr]を使ってブール式が正ユネイトかどうか検定することができる.
- 事象の信頼性分布 distiはPDF[disti,t]が t≤0のときにゼロの一変量分布でなければならない.
- 事象識別子 xiのFailureDistribution[bexpr,…]
-
xiTrue 事象 xiが起ったことを示す xiFalse 事象 xiがまだ起っていないことを示す - 時間 t におけるFailureDistribution[bexpr,{{x1,dist1},…}]の累積分布関数はProbability[bexpr/.{x1->t1≤t,…},{t1dist1,…}]で与えられる.
- FailureDistributionは,Mean,SurvivalFunction,HazardFunction,RandomVariate等の関数とともに使うことができる.
例題
すべて開くすべて閉じる例 (3)
スコープ (22)
基本的な用法 (5)
2つの事象のどちらかが起った場合に故障する系の故障までの平均時間を求める:
2つの事象が両方とも起った場合に故障する系の生存関数を求める:
3つの事象のうち2つの事象が起った場合に故障する系のSurvivalFunctionを求める:
構造関数 (4)
UnateQを使ってブール式が正ユネイトであるかどうか検定する:
パラメトリック寿命分布 (4)
LogNormalDistributionを含む任意のパラメトリック寿命分布を使う:
1つの事象がかなり遅れて起る場合,この事象が系の寿命を決定する:
OrゲイトとAndゲイトがある系をこれらの分布とともに定義する:
SurvivalFunctionをプロットする:
ノンパラメトリック寿命分布 (3)
SmoothKernelDistributionを使って航空機のガラス強度をモデル化する:
航空機のガラスが割れるか他の事象が起るかすると故障する系について考える:
HistogramDistributionを使って事象をモデル化する:
2つないし3つの事象があるOrゲートについての生存関数をプロットする:
EmpiricalDistributionを使って直接データから事象をモデル化する:
派生寿命分布 (6)
StandbyDistributionで事象をモデル化する:
SurvivalFunctionをプロットする:
StandbyDistributionで事象をモデル化する:
1つの事象がParameterMixtureDistributionである系:
MixtureDistributionで2要素のコールドスタンバイ系をモデル化する:
これをFailureDistributionで使って生存関数を計算する:
StandbyDistributionとの等価性を示す:
OrderDistributionを使って事象の寿命をモデル化することができる:
SurvivalFunctionをプロットする:
アプリケーション (6)
朝起きられないリスクをモデル化する.古くなった目覚まし時計をバックアップとして持っていると仮定する:
1年目のある時点で(目覚ましが鳴らないために)起きられない確率を求める:
炭鉱での問題の一つに,石炭の山の間の空洞に渡した橋からブルドーザーが落ちることがある.ブルドーザーは空洞の存在を知った上でその上に来ることもあれば,知らずに来ることもある:
空洞は石炭の地中流出によって形成される.これは,コンベヤーベルトの下から石炭を搬出し開放供給機を撤去することで生じる:
地表に流れがないことも原因となる.石炭が凍結すると地表の流れが止まる:
1つの堆積山で事象が発生するまでの平均時間はおよそ60年である:
水中のパイプラインの修理は水面下のドライメンテナンスキャビンを使って行われる.生命維持装置の部品の故障までの平均時間(単位:時間)とその寿命分布 ![]() は以下で与えられる:
は以下で与えられる:
典型的な作業時間は24時間である.作業の生存確率を計算する:
地球を巡る軌道上の宇宙船に推進力を与える推進装置について考える.デバイスのスイッチを切ってから推進力を与える事象をモデル化する:
望まない推進力が6ヶ月間のミッション中に生じる確率を求める:
5日間のミッション中に故障しないように確率![]() で故障率
で故障率 ![]() となる必要条件を求める:
となる必要条件を求める:
FailureDistributionは一般化されたOrderDistributionとして使うことができる:
同一分布が使われた場合,これはOrderDistributionに等しい:
特性と関係 (12)
FailureDistributionは入力中の変数に局所名を使う:
したがって,続く計算はもとの変数名を使って行うことができる:
これはOrゲートに対応する:
これはAndゲートに対応する:
同一事象を繋ぐOrゲートはOrderDistributionに対応する:
同一事象を繋ぐAndゲートはOrderDistributionに対応する:
同一事象を伴うボーティングゲートはOrderDistributionに対応する:
Orゲートで繋がれた基本事象の寿命は部品の寿命の最低のものである:
Andゲートで繋がれた2つの事象の寿命はその事象の寿命の最大のものである:
![]() アウトオブ
アウトオブ ![]() のボーティングゲートはRankedMin関数を伴うTransformedDistributionに対応する:
のボーティングゲートはRankedMin関数を伴うTransformedDistributionに対応する:
Orゲートで繋がれた指数分布に従う事象は指数的な頂上事象を与える:
Orゲートで繋がれたワイブル(Weibull)分布に従う事象はワイブル分布に従う頂上事象を与える:
FailureDistributionは ![]() あるいは
あるいは ![]() が故障すると頂上事象が起ることをモデル化する:
が故障すると頂上事象が起ることをモデル化する:
ReliabilityDistributionは系が動くためには両方の部品が動かなくてはならないことをモデル化する:
部品 ![]() と
と ![]() が動くことは
が動くことは ![]() と
と ![]() のどちらかが故障することに等しい:
のどちらかが故障することに等しい:
考えられる問題 (3)
TruncatedDistributionを使って正の値のみに領域を限定する:
FailureDistributionは正ユネイト構造式についてのみ明確に定義することができる:
UnateQを使ってブール式が正ユネイトかどうか検定する:
テキスト
Wolfram Research (2012), FailureDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/FailureDistribution.html.
CMS
Wolfram Language. 2012. "FailureDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FailureDistribution.html.
APA
Wolfram Language. (2012). FailureDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FailureDistribution.html