FailureDistribution
FailureDistribution[bexpr,{{x1,dist1},{x2,dist2},…}]
表示一个系统的失效分布,其中事件 xi 的可靠性分布为 disti,当布尔表达式 bexpr 为 True 时发生顶级事件而当 xi 为 True 时事件 xi 发生.
更多信息

- FailureDistribution[bexpr,…] 对应于故障树规范.
- 布尔表达式 bexpr 也称为系统的结构函数.
- 典型的结构函数包括:
-
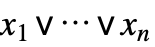
Or 门 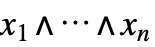
And 门 ![TemplateBox[{BooleanCountingFunction, paclet:ref/BooleanCountingFunction}, RefLink, BaseStyle -> {2ColumnTableMod}][{k,n},n] TemplateBox[{BooleanCountingFunction, paclet:ref/BooleanCountingFunction}, RefLink, BaseStyle -> {2ColumnTableMod}][{k,n},n]](Files/FailureDistribution.zh/3.png)
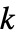 -
-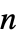 系统
系统BooleanConsecutiveFunction[k,n] 连续的 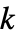 -
-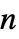 系统
系统 - 结构函数 bexpr 可以是任意正的单边布尔函数.
- UnateQ[bexpr] 可用于测试布尔表达式是否是正单边的.
- 事件可靠性分布 disti 必须是 PDF[disti,t] 下的单变量分布,对于 t≤0 是零.
- 对于具有事件指示器 xi 的 FailureDistribution[bexpr,…]:
-
xiTrue 表明事件 xi 已经发生 xiFalse 表明事件 xi 没有发生 - 对于 FailureDistribution[bexpr,{{x1,dist1},…}],时间 t 处的累积分布函数由Probability[bexpr/.{x1->t1≤t,…},{t1dist1,…}] 给出.
- FailureDistribution 可以与诸如 Mean、SurvivalFunction、HazardFunction 和 RandomVariate 等函数一起使用.
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (22)
基本用途 (5)
对于一个当两个事件中任何一个发生时,就发生故障的系统,求故障发生前的平均时间:
对三个事件中有两个发生时,才出现故障的系统,求该系统的 SurvivalFunction:
结构函数 (4)
使用 UnateQ 来测试一个布尔表达式是否是正单边的:
参数式寿命分布 (4)
使用任何参数式寿命分布,包括 LogNormalDistribution:
绘制 SurvivalFunction 的图线:
非参数式寿命分布 (3)
使用 SmoothKernelDistribution 对飞机玻璃强度建模:
使用 HistogramDistribution 对事件建模:
在两个和三个事件下,绘制 Or 门的生存函数的图线:
使用 EmpiricalDistribution 直接从数据对事件建模:
导出寿命分布 (6)
使用 StandbyDistribution 对事件建模:
绘制 SurvivalFunction 的图线:
使用 StandbyDistribution 对事件建模:
有一个事件是 ParameterMixtureDistribution 的系统:
使用 MixtureDistribution 对双元件冷却贮备系统建模:
在 FailureDistribution 中使用它,并且计算生存函数:
使用 StandbyDistribution 显示等价性:
OrderDistribution 可用于对事件寿命建模:
绘制 SurvivalFunction 的图线:
应用 (6)
在煤矿发生的一个问题是推土机通过桥接空隙掉在煤堆中. 推土机可以有意或无意地形成一个空隙(void):
若要形成一个空隙(void),煤中必须有地下水流. 这要求在传送带上从下面去除煤,并且形成到传送带的一个开放供给装置:
地下水干式维修舱是用于维修地下水管道的. 寿命支持系统的元件出现故障的平均时间(以小时为单位)和他们的寿命分布 ![]() 如下所示:
如下所示:
考虑对环绕地球的轨道上的车辆提供推力的推进系统. 我们对在设备关闭后应用推力的事件建模:
FailureDistribution 可以作为一个广义 OrderDistribution 使用:
如果使用相同的分布,这等于 OrderDistribution:
属性和关系 (12)
FailureDistribution 对输入中的变量使用局部名称:
这对应于 Or 门:
这对应于一个 And 门:
连接相同事件的 Or 门对应于 OrderDistribution:
连接相同事件的 And 门对应于 OrderDistribution:
具有相同事件的表决门对应于 OrderDistribution:
Or 门连接的基本事件的寿命是元件寿命的最小值:
使用 And 门连接的两个事件的寿命是事件寿命的最大值:
![]() 取
取 ![]() 表决门对应于 TransformedDistribution,其中使用 RankedMin 函数:
表决门对应于 TransformedDistribution,其中使用 RankedMin 函数:
使用 Or 门连接的指数分布事件给出指数分布的顶级事件:
Or 门连接的威布尔分布事件给出威布尔分布的顶级事件:
FailureDistribution 模型,如果 ![]() 或者
或者 ![]() 出现故障,则出现顶级事件:
出现故障,则出现顶级事件:
ReliabilityDistribution 模型,系统要运行需要两个元件都运行:
可能存在的问题 (3)
文本
Wolfram Research (2012),FailureDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FailureDistribution.html.
CMS
Wolfram 语言. 2012. "FailureDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FailureDistribution.html.
APA
Wolfram 语言. (2012). FailureDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FailureDistribution.html 年