



FindFit
詳細とオプション




- data の形は{{x1,y1,…,f1},{x2,y2,…,f2},…}でよい.ただし,座標 x, y, …の数はリスト vars 中の変数の数に等しいものとする.
- data の形は{f1,f2,…}でもよい.この場合,座標は1つで1, 2, …の値を取ると仮定される.
- FindFitは par1, par2, …に代入するもののリストを返す.
- 式 expr は pars と vars がすべて数値であるときは数値を返さなければならない.
- 式 expr は線形的にあるいは非線形的に pariに依存することができる.
- 制約条件 cons は,等式,不等式,あるいはそれらの論理結合を含むことができる.
- 線形的な場合,FindFitは大域的な最適フィットを求める.
- 非線形的な場合,FindFitは通常局所的な最適フィットしか求めない.
- FindFit[data,expr,{{par1,p1},{par2,p2},…},vars]は{par1->p1,par2->p2,…}でフィットの探索を始める.
- FindFitはデフォルトで最小二乗フィットを求める.
- 次は,使用可能なフィットの特性"prop"である.
-
"BestFit" 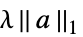
基本関数の最適フィット線形結合 "BestFitParameters" 
最適フィットを与えるベクトル 
"Coordinates" {{x1,y1,…},…} data における vars の座標 "FitResiduals" 
座標におけるモデルとフィットの差 "Function" Function[{x,y,…},a1 f1+…+an fn] 最適フィット純関数 "PredictedResponse" 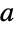
data 座標のフィットされた値 "Response" 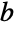
入力 data からの応答ベクトル 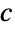
{"prop1","prop2",…} いくつかのフィット特性 - オプションNormFunction->f はノルム f[residual]が最小になるように指定する.
- 可能なオプション
-
AccuracyGoal Automatic 目標となる確度 EvaluationMonitor None expr が評価されたときに常に評価される式 FitRegularization None モデルの pars の正規化 Gradient Automatic expr の勾配要素のリスト MaxIterations Automatic 使用する最大反復回数 Method Automatic 使用されるアルゴリズム NormFunction Norm 最小化のノルム PrecisionGoal Automatic 目標となる精度 StepMonitor None 段階を取るたびに常に評価される式 WorkingPrecision Automatic 内部計算で使用する精度 - AccuracyGoalとPrecisionGoalのデフォルト設定はWorkingPrecision/2である.
- AccuracyGoalとPrecisionGoalの設定は返されるパラメータの値とNormFunctionの値の両方における目標桁数を指定する.
- NormFunction->f でFitRegularization->rfun のとき,Fitは normf[{expr(pars,x1,y1,…)-f1,…}]+rfun[pars]を最小にする pars の値を求める.
- NormFunctionの設定は以下の形で与えることができる.
-
f 剰余に適用される関数 f {"HuberPenalty",α} 各成分についてのHuberペナルティ関数の合計 {"DeadzoneLinearPenalty",α} 各成分についてのデッドゾーン線形ペナルティ関数の合計 - FitRegularizationの設定は以下の形で与えることができる.
-
None 正規化は行わない rfun rfun[a]による正規化 {"Tikhonov", λ} 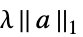 による正規化
による正規化{"LASSO",λ}  による正規化
による正規化{"Variation",λ} ![lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||^2 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||^2](Files/FindFit.ja/11.png) による正規化
による正規化{"TotalVariation",λ} ![lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||_1 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||_1](Files/FindFit.ja/12.png) による正規化
による正規化{"Curvature",λ} ![lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a,2]||^2 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a,2]||^2](Files/FindFit.ja/13.png) による正規化
による正規化{r1,r2,…} r1,…からの項の合計による正規化 - FindFitはAccuracyGoalまたはPrecisionGoalで指定された目標が達成されるまで続ける.
- Methodの可能な設定値には,"ConjugateGradient","PrincipalAxis","LevenbergMarquardt","Newton","NMinimize","QuasiNewton"等がある.デフォルト値はAutomaticである.
例題
すべて開く すべて閉じるスコープ (7)
簡単な指数フィット (3)
制約条件と初期値 (2)
オプション (7)
Gradient (1)
MaxIterations (1)
Method (1)
StepMonitor (1)
WorkingPrecision (1)
より正確なパラメータの予測を得るためにより高い作業精度(WorkingPrecision)を使う:
アプリケーション (7)
実験データ (3)
微分方程式 (2)
微分方程式モデルにおける最高のフィットを与えるパラメータを求める:
パラメータ![]() の集合についての解がすべての
の集合についての解がすべての ![]() の値について再利用できるようにモデルを定義する:
の値について再利用できるようにモデルを定義する:
常微分方程式の解の精度について適当な許容度のフィットを求める:
KdV方程式の非ソリトン初期条件がどのように2つのソリトンに分解するかを求める:
偏微分方程式を解くためにNDSolveで使われる空間格子を得る:
特性と関係 (6)
FindFitはパラメータ推定を与える:
NonlinearModelFitを使ってフィットに関する追加的な除法の抽出することができる:
線形モデルにとって,FitとFindFitは等価でありLeastSquaresを使う:
底{1,x,x2}でFitを使う:
これはモデル関数が基底の線形結合であるFindFitに等しい:
計画行列を構築しLeastSquaresを使って係数を求める:
LinearModelFitは線形モデルをフィットし,フィットに関する追加的な情報を返す:
FindFitは実質的にFindMinimumを使って剰余関数のノルムを最小化する:
FindFitはデフォルトで正規分布した応答と矛盾しない結果を返す:
LogitModelFitは二項分布した応答を想定する:
ProbitModelFitについても同じことが言える:
GeneralizedLinearModelFitは二項分布およびその他の分布構造を許容する.
FindFitは,TimeSeriesのタイムスタンプを変数として用いる:
FindFitは複数経路のTemporalDataについて経路ごとに働く:
関連項目
FindMinimum Fit FindFormula NMinimize LeastSquares Interpolation FindCurvePath ChiSquareDistribution LinearModelFit NonlinearModelFit
Function Repository: TrigFit
テクニカルノート
-
▪
- 数値データの分析 ▪
- 曲線のフィット ▪
- 制約条件付き最適化 ▪
- 制約条件のない最適化 ▪
- 実装に関するノート: 数値および関連関数
関連するガイド
-
▪
- 曲線のフィットと近似の関数 ▪
- 時系列の処理 ▪
- データの変換と平滑化 ▪
- 行列ベースの最小化 ▪
- 教師あり機械学習 ▪
- 最適化 ▪
- 科学的データ解析 ▪
- 数値データ ▪
- 機械学習 ▪
- 信号の可視化と解析 ▪
- 顕微鏡検査のための画像計算
履歴
2003 で導入 (5.0) | 2007 で更新 (6.0) ▪ 2019 (12.0) ▪ 2025 (14.2)
テキスト
Wolfram Research (2003), FindFit, Wolfram言語関数, https://reference.wolfram.com/language/ref/FindFit.html (2025年に更新).
CMS
Wolfram Language. 2003. "FindFit." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/FindFit.html.
APA
Wolfram Language. (2003). FindFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindFit.html
BibTeX
@misc{reference.wolfram_2025_findfit, author="Wolfram Research", title="{FindFit}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/FindFit.html}", note=[Accessed: 21-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_findfit, organization={Wolfram Research}, title={FindFit}, year={2025}, url={https://reference.wolfram.com/language/ref/FindFit.html}, note=[Accessed: 21-February-2026]}