FourierMatrix

FourierMatrix[n]

n×n フーリエ(Fourier)行列を返す．

詳細とオプション

  • 次数 n のFourierMatrixは長さ n の離散フーリエ変換の基底数列のリストを返す．
  • フーリエ行列の各項は，デフォルトで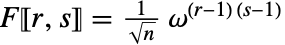，と定義される．ただし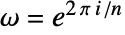，である．
  • FourierMatrixの行は離散フーリエ変換の基底数列である．
  • FourierMatrix[n]の結果 F は複素対称でユニタリである．つまり，F-1はConjugate[F]である．
  • 次は使用可能なオプションである．
  • FourierParameters {0,1}フーリエ変換を定義するパラメータ
    TargetStructure Automatic返される行列の構造
    WorkingPrecision Infinity成分を構築する精度
  • オプションFourierParametersを使うとフーリエ行列の異なる定義が指定できる．FourierParameters->{a,b}の定義では，フーリエ行列の項は 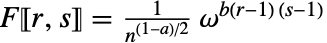と定義される．ただし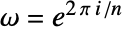，である．
  • よく使われる{a,b}の選択肢には，{0,1}（物理），{-1,1}（データ解析），{1,-1}（信号処理）がある．
  • 次は，TargetStructureの可能な設定である．
  • Automatic返す表現を自動選択する
    "Dense"行列を密な行列として表す
    "Structured"行列を構造化配列として表す
    "Symmetric"行列を対称行列として表す
    "Unitary"行列をユニタリ行列として表す
  • FourierMatrix[…,TargetStructureAutomatic]のとき，行列の成分数が現行の閾値未満の場合は密な行列が返され，それ以外の場合は構造化配列が返される．
  • FourierMatrix[n].list の結果は，list の長さが n のときはFourier[list]の結果に等しい．しかし，FourierMatrixが構造化配列のまま保持されない限りFourier[list]の計算の方がはるかに高速で数値誤差も小さい． »
  • 構造化FourierMatrix sa については，以下の特性"prop"に sa["prop"]でアクセスすることができる．
  • "FourierParameters"パラメータ{a,b}
    "WorkingPrecision"内部精度
    "Properties"サポートされる特性のリスト
    "Structure"構造化配列の型
    "StructuredData"構造化配列に格納された内部データ
    "StructuredAlgorithms"構造化配列に対して特別なメソッドを持つ関数のリスト
    "Summary"Datasetとして表される情報の要約

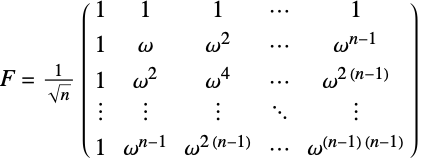
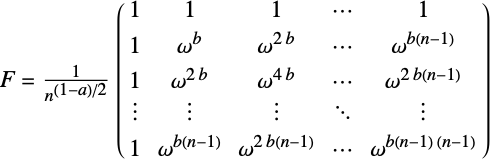
例題

すべて開くすべて閉じる

例  (2)

フーリエ行列：

大きいフーリエ行列：

スコープ  (2)

長さ128のフーリエ基底数列の実数部分と虚数部分：

オプション設定TargetStructure"Structured"を使って構造化フーリエ行列を構築する：

構造化表現を使うと，大きい行列の場合はメモリが大幅に節約できる：

オプション  (3)

FourierParameters  (1)

フーリエ行列のデフォルトの定義：

信号処理に使われるフーリエ行列の定義を使う：

データ解析に使われるフーリエ行列の定義を使う：

TargetStructure  (1)

フーリエ行列を密な行列として返す：

フーリエ行列を構造化配列として返す：

フーリエ行列を対称行列として返す：

フーリエ行列をユニタリ行列として返す：

WorkingPrecision  (1)

機械精度を使う：

任意精度を使う：

アプリケーション  (3)

高速フーリエ変換(FFT)の効率は2つの小さいフーリエ行列から1つの大きいフーリエ行列を構築できることによる．大きさ p が q との2つの小さいフーリエ行列を生成する：

大きさが p q のフーリエ行列はより簡単な4つの行列の積として表すことができる：

結果の行列がFourierMatrixの結果と等しいことを示す：

ベクトルの離散フーリエ変換はフーリエ行列の係数を連続的にベクトルに掛けることで計算できる：

結果はFourierをベクトルに適用したものに等しい：

ベクトルから巡回行列を構築する関数を定義する：

巡回行列はフーリエ行列によって対角化できる：

結果の対角行列の対角要素はフーリエ行列と開始ベクトルの積に一定のスケーリング係数まで等しい：

単位を正規化したフーリエ行列：

偶数次元の場合は，行列の永久式は0である：

奇数次元の場合は，行列の永久式は常に整数である：

p>3の奇整数の場合は，p×p 行列の永久式は p3を法として p!と一致する：

特性と関係  (2)

FourierMatrixはスケールされたVandermondeMatrixとして表すことができる：

ベクトルのフーリエ変換はベクトルにフーリエ行列を掛けたものと等価である：

逆フーリエ変換は共役転置倍するのに等しい：

Fourierは行列に基づいた計算よりもはるかに速い：

Wolfram Research (2012), FourierMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/FourierMatrix.html （2024年に更新）.

テキスト

Wolfram Research (2012), FourierMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/FourierMatrix.html （2024年に更新）.

CMS

Wolfram Language. 2012. "FourierMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/FourierMatrix.html.

APA

Wolfram Language. (2012). FourierMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierMatrix.html

BibTeX

@misc{reference.wolfram_2024_fouriermatrix, author="Wolfram Research", title="{FourierMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FourierMatrix.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fouriermatrix, organization={Wolfram Research}, title={FourierMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/FourierMatrix.html}, note=[Accessed: 14-November-2024 ]}