FunctionMeromorphic

FunctionMeromorphic[f,x]

が x の有理型関数かどうかを判定する．

FunctionMeromorphic[f,{x1,x2,…}]

が x1,x2,…の有理型関数かどうかを判定する．

FunctionMeromorphic[{f1,f2,…},{x1,x2,…}]

が x1,x2,…の有理型関数かどうかを判定する．

FunctionMeromorphic[{funs,cons},xvars]

が制約 cons の解を含む開集合で xvars の有理型関数かどうかを判定する．

詳細とオプション

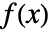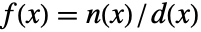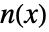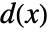  • 関数 が として表せるなら，その関数は解析的である．ただし，と は複素解析関数である．
  • 関数 が局所的に 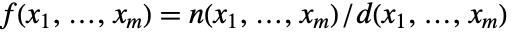として表せるなら，その関数は有理型である．ただし，と は複素解析関数である．
  • funs が xvars 以外のパラメータを含むとき，結果はConditionalExpressionになることが多い．
  • cons は，不等式あるいはそれらの論理結合を含むことができる．
  • 次は，使用可能なオプションである．
  • Assumptions $Assumptionsパラメータについての仮定
    GenerateConditions Trueパラメータについての条件を生成するかどうか
    PerformanceGoal $PerformanceGoal速度あるいは品質を優先するかどうか
  • 次は，GenerateConditionsの可能な設定である．
  • Automatic一般的ではない条件のみ
    Trueすべての条件
    False条件なし
    None条件が必要な場合は未評価で返す
  • PerformanceGoalの可能な設定は"Speed"と"Quality"である．

例題

すべて開くすべて閉じる

例  (3)

一変量関数が有理型かどうかを判定する：

多変量関数が有理型かどうかを判定する：

関数が制限された領域上で有理型かどうかを判定する：

スコープ  (4)

一変量関数：

唯一の特異点は極である：

は有理型ではない：

これは，負の実数軸に分枝切断線を持つ：

領域に制限がある関数：

正の虚軸に沿った分枝切断は制限領域の外にある：

多変量関数：

記号パラメータを持つ関数：

オプション  (4)

Assumptions  (1)

FunctionMeromorphicはパラメータ の任意の値に対する答は求められない：

が正の整数であるという仮定があると，FunctionMeromorphicは成功する：

GenerateConditions  (2)

デフォルトで，FunctionMeromorphicは記号パラメータについての条件を生成する：

GenerateConditions->Noneとすると，FunctionMeromorphicは条件付きの結果を出せずに失敗する：

以下は，条件を述べずに条件付きで有効な結果を返す：

デフォルトで，すべての条件が報告される：

GenerateConditions->Automaticとすると，一般的に真である条件は報告されない：

PerformanceGoal  (1)

PerformanceGoalを使って潜在的に高くつく計算を避ける：

デフォルト設定は使用可能なすべてのテクニックを使って結果を出そうとする：

アプリケーション  (12)

有理型関数のクラス  (7)

有理関数は有理型である：

Tan，Sec，Sechは有理型である：

これらの関数を可視化する：

平面で関数を可視化するとその特異点が極より悪くないことが分かる：

Logのように分枝切断線がある関数は有理型ではない：

どちらもSqrtでも任意の非整数ベキでもない：

ArcSin，ArcTan，ArcCsch等の逆三角関数と双曲線関数は，同様に有理型ではない：

Abs，Sign，Reのような微分不可能な関数は有理型ではない：

これらの関数のいくつかを可視化する：

UnitStepおよびTriangleWaveのように実数入力に対してのみ定義される関数は，有理型ではありえない：

これらの関数は複素数値については定義されない：

複素平面で解析的な関数はすべて有理型である：

有理関数の算術的な組合せは有理型である：

三角関数と双曲線関数はすべてExpの算術的組合せなので，これらはすべて有理型である：

より一般的には，有理型関数の任意の有理結合は有理型である：

Expおよび8つの非有理型の三角関数と双曲線関数を可視化する：

有理型関数の合成関数は有理型である必要はない：

有理型関数の特異点は合成の下で束になり，極ではない特異点になる可能性がある：

以下の極限によって証明されるように，原点に真性特異点がある：

しかし，有理型関数と解析関数の合成は常に有理型である：

合成関数を可視化する：

多変量有理関数は有理型である：

一変数の関数とは異なり，特異点は曲線に沿って，最初の関数では に沿って，存在する：

2番目の関数を平面でプロットすると，双曲線に沿った爆発が見られる：

一変量解析関数と合成することで，さらに多くの解析関数が生成される：

完全Beta関数TemplateBox[{x, y}, Beta]は有理型である：

これは，Gammaにおける多変量有理関数と考えられる：

関数を可視化する：

関数の積分  (5)

有理型関数のLimitは常に数かComplexInfinityかである：

Sqrtには極限が存在しない点があるので，有理型ではない：

極と呼ばれる有理型関数の特異点は，関連付けられたResidueを持つ：

留数は，関数のベキ級数展開におけるの係数である：

有理型関数の閉じた輪郭線の周りの積分は，曲線に囲まれた極の留数の総和の 倍に等しい．明らかにその唯一の極である，原点の周りのの積分を計算する：

これは，における留数の 倍と等しくなければならない：

例えば円のようなその他の任意の閉じた曲線も同じ結果を与える：

関数とその輪郭線を可視化する：

輪郭線が特異点を囲まなければ，積分は0になる：

別の輪郭線で関数を可視化する：

関数のすべての特異点が同じあるいは関連した留数を持つなら，閉じた輪郭線の積分を使って囲い込まれた極の数が数えられる．例えば，は， のすべての半整数倍で留数で極を持つ：

実軸にまたがる長方形上のの積分は，囲まれた の半整数倍の数を数える：

周回積分の一般的な用途は，上半平面または下半平面に半円がある閉じた曲線に周回を拡張することで実線上で積分を評価することである．半円上の積分の部分が消える場合は，周回積分は実数積分と等しくなければならない． について考える．被積分関数は有理型である：

被積分関数の特異点は分母が0になるところである：

上半平面上の半円を使って周回を完成させ，留数を使って積分を計算する：

のときの半円上の積分の次数は なので，実数積分は同じ値にならなけらばならない：

での形の被積分関数（ は有理型でTemplateBox[{}, Reals]上で連続であり，大きいTemplateBox[{z}, Abs]についてTemplateBox[{{f, (, z, )}}, Abs]<C/(TemplateBox[{z}, Abs])）について，積分 は上半平面上の の留数の和の 倍として計算できる．これを使って を計算する．まず，が有理型であることを確認する：

この関数は，必要に応じて無限大において減衰する：

上半平面には に単一の極がある：

したがって，積分 ：

とは偶数なので， は前の結果の半分である：

直接計算で結果を確かめる：

特性と関係  (5)

有理型関数は何度でも微分することができる：

Dを使って導関数を計算する：

有理型関数はその定義域の各点でテイラー(Taylor)級数として表現できる：

Seriesを使ってテイラー級数の初期項を計算する：

結果の多項式はの近くで を近似する：

この関数は，その極において有限な主要部を持つローラン(Laurent)級数として表すことができる：

有理型関数はコンパクト領域では有限個の0点と極しか持つことができない：

Solveを使って単位円板上で の零点を求める：

FunctionSingularitiesを使って単位円板上で の極を求める：

零点（青）と極（赤）で をプロットする：

偏角の原理には，零点の数と の極の数（多重度で数えられる）の差は で与えられるとある．NIntegrateを使って を計算する：

すべての が の単純零点であることを確かめる：

Limitを使ってすべての が の単純極であることを確かめる：

を直接計算する：

複素解析関数の商は有理型である：

FunctionAnalyticを使って と が解析的であることを確かめる：

と が有理型であることを確かめる：

有理型関数は複素解析的ではないかもしれない：

有理型関数が持ちうる唯一の特異点は極と加除特異点である：

FunctionSingularitiesを使ってすべての特異点が満足する条件を求める：

SolveValuesを使って特異点を求める：

FunctionPolesを使って極とその多重度を求める：

ResidueSumを使って右半平面の留数の和を計算する：

Wolfram Research (2020), FunctionMeromorphic, Wolfram言語関数， https://reference.wolfram.com/language/ref/FunctionMeromorphic.html.

テキスト

Wolfram Research (2020), FunctionMeromorphic, Wolfram言語関数， https://reference.wolfram.com/language/ref/FunctionMeromorphic.html.

CMS

Wolfram Language. 2020. "FunctionMeromorphic." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionMeromorphic.html.

APA

Wolfram Language. (2020). FunctionMeromorphic. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionMeromorphic.html

BibTeX

@misc{reference.wolfram_2024_functionmeromorphic, author="Wolfram Research", title="{FunctionMeromorphic}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionMeromorphic.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_functionmeromorphic, organization={Wolfram Research}, title={FunctionMeromorphic}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionMeromorphic.html}, note=[Accessed: 21-November-2024 ]}