Graphおよび関連関数のオプションで,使用するレイアウトを指定する.


GraphLayout
グラフレイアウトのリスト »Graphおよび関連関数のオプションで,使用するレイアウトを指定する.
詳細





- グラフレイアウトの計算は通常数段階で行われる.GraphLayout->{s1->m1,…}とすると,段階 siにメソッド miが使われる.
- 次は,グラフレイアウトに使用可能な段階 siである.
-
"VertexLayout" 頂点をどのように埋め込むか "EdgeLayout" 辺の順序をどのように決めるか "PackingLayout" 頂点の連結成分をどのように置くか - 次は,"VertexLayout"メソッドである.
-
Automatic レイアウトを自動的に選択する None レイアウトは計算しない "emb" 名前付きの埋込み - 次は,使用可能な特別埋込み"emb"である.
-

"BipartiteEmbedding" 頂点を2本の平行線上に置く 
"CircularEmbedding" 頂点を円の上に置く 
"CircularMultipartiteEmbedding" 頂点を円の弦の上に置く 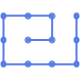
"DiscreteSpiralEmbedding" 頂点を離散螺線上に置く 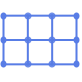
"GridEmbedding" 頂点を格子上に置く 
"LinearEmbedding" 頂点を直線上に置く 
"MultipartiteEmbedding" 頂点を数本の平行線上に置く 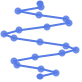
"SpiralEmbedding" 頂点を2Dに投影された3D螺線の上に置く 
"StarEmbedding" 頂点を中心のある円上に置く - 次は,木グラフ等の層状グラフと有向非巡回グラフのための使用可能な構造埋込み"emb"である.
-

"BalloonEmbedding" 頂点を中心が親頂点上にある円上に置く 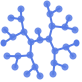
"RadialEmbedding" 頂点を円弧の一部に置く 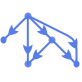
"LayeredDigraphEmbedding" 頂点を有向非巡回グラフの平行線上に置く 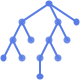
"LayeredEmbedding" 頂点を平行線上に置く 
"SymmetricLayeredEmbedding" 対称平行線上の頂点 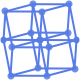
"HyperbolicRadialEmbedding" ポアンカレ円板上の円弧上の頂点 - 使用可能な最適化埋込み"emb"は,どれも数量を最少にする.以下は含まれるものである.
-
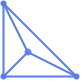
"GravityEmbedding" 頂点を質点,辺をバネとするエネルギー 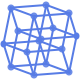
"HighDimensionalEmbedding" 高次元のバネ電気のエネルギー 
"PlanarEmbedding" 辺交差の数 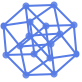
"SpectralEmbedding" 平方距離の重み付きの総和 
"SphericalEmbedding" 曲面上の頂点とバネとしての辺を持つエネルギー 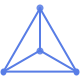
"SpringElectricalEmbedding" 辺をバネ,頂点を電荷とするエネルギー 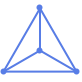
"SpringEmbedding" 辺をバネとするエネルギー 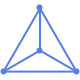
"TutteEmbedding" 辺交差の数と近傍までの距離 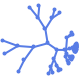
"HyperbolicSpringEmbedding" ポアンカレ円板上のバネとしての辺を持つエネルギー - 次は,"EdgeLayout"メソッドの可能な設定値である.
-
"DividedEdgeBundling" 辺を線分の束に分ける "HierarchicalEdgeBundling" 階層的木構造に従って辺を束にする "StraightLine" 辺の間の直線 - 次は,"PackingLayout"の可能な設定値である.
-
"ClosestPacking" 最上部左からの最密充填を近似する "ClosestPackingCenter" 中央からの最密充填を近似する "Layered" 最上部左から始めて層に並べる "LayeredLeft" 左から始めて層に並べる "LayeredTop" 最上部から始めて層に並べる "NestedGrid" ネストした格子上に並べる
例題
すべて開く すべて閉じるスコープ (131)
基本的な用法 (3)
頂点のレイアウト (116)
"BalloonEmbedding" (8)
"BalloonEmbedding"は木グラフに最適である:
オプション"EvenAngle"->Trueを使って囲み円の中に頂点を均等に置く:
"OptimalOrder"->Trueと設定すると,頂点の並び順が角度分解能と縦横比を最適化する:
オプション"RootVertex"->v を使って根頂点を設定する:
オプション"Rotation"->r を使ってレイアウトを回転させる:
"BipartiteEmbedding" (2)
"CircularEmbedding" (4)
"CircularEmbedding"は,巡回グラフ,LCF表記の埋込み,閉路グラフに最適である:
"CircularMultipartiteLayout" (3)
"CircularMultipartiteEmbedding"は k 部グラフに最適である:
"DiscreteSpiralEmbedding" (3)
"DiscreteSpiralEmbedding"は道グラフに最も適している:
"GravityEmbedding" (2)
"GridEmbedding" (3)
"HighDimensionalEmbedding" (3)
"HighDimensionalEmbedding"は大きいグラフに最適である:
"HyperbolicRadialEmbedding" (4)
"HyperbolicRadialEmbedding"は木グラフに最も適している:
"HyperbolicSpringEmbedding" (10)
"HyperbolicSpringEmbedding"は,木グラフに最も適している:
"EdgeWeighted"Trueと設定すると,辺の重みが使われる:
オプション "EnergyControl"e を使って,最小化の過程におけるシステム全体のエネルギーに対する制約を指定する:
"InferentialDistance"d を使って頂点間の相互作用が存在しないと仮定されるカットオフ距離を指定する:
"MaxIteration"it を使ってエネルギーの最小化を試みる際に使用される反復回数の上限を指定する:
"RandomSeed"int を使って,初期頂点配置を計算する乱数生成器のシードを指定する:
"StepControl"method を使ってエネルギー最小化の際のステップ長の変更方法を定義する:
"LayeredEmbedding" (7)
非隣接層間の辺の数を最小にするような方法で,いくつかの層に頂点を置く:
"LayeredEmbedding"は木グラフに最も適している:
オプション"LayerSizeFunction"->func を使って相対的な高さを指定する:
オプション"RootVertex"->v を使って根頂点を設定する:
オプション"LeafDistance"->d を使って葉の距離を指定する:
"LayeredDigraphEmbedding" (7)
"LayeredDigraphEmbedding"は有向非巡回グラフに最適である:
オプション"RootVertex"->v を使って根頂点を設定する:
オプション"Rotation"r を使ってレイアウトを回転させる:
オプション"Orientation"->o を使って方向が違う木を描画する:
"LinearEmbedding" (2)
"MultipartiteEmbedding" (3)
"MultipartiteEmbedding"は k 部グラフに最適である:
"PlanarEmbedding" (2)
"RadialEmbedding" (5)
"RadialEmbedding"は木グラフに最も適している:
オプション"RootVertex"->v を使って根頂点を設定する:
"SpectralEmbedding" (3)
"SphericalEmbedding" (2)
"SpiralEmbedding" (3)
"SpringElectricalEmbedding" (15)
各頂点が荷電していて各辺がバネに対応するときに,力学的エネルギーと電気エネルギーが最小になるように頂点を並べる:
"SpringElectricalEmbedding"は大多数のグラフに非常に適している:
"EdgeWeighted"->Trueと設定すると,辺の重みが使われる:
オプション"EnergyControl"->e を使って最小化の際の系の総エネルギーについての制限を指定する:
"InferentialDistance"->d を使ってカットオフ距離を指定する.このカットオフ距離を超えた頂点間のインタラクションは存在しないと想定される:
"MaxIteration"->it を使ってエネルギーの最小化の試みに使う最大反復回数を指定する:
"Multilevel"->method を使ってグラフを粗大化させる再帰的手続きに使うメソッドを指定する:
"Octree"->Trueと設定すると,八分木データ構造(三次元)あるいは四分木データ構造(二次元)が反発力の計算に使われる:
"RandomSeed"->int を使って最初の頂点の置き方を計算する乱数生成器のシードを指定する:
"RepulsiveForcePower"->r を使って,反発力が距離によって減衰する速さを制御する:
オプション"Rotation"r を使ってレイアウトを回転させる:
"SpringConstant"r を使って引力の定数を制御する:
"StepControl"->method を使ってエネルギーの最小化において刻み幅がどのように調整されるかを定義する:
"SpringEmbedding" (12)
各辺がバネに対応するときの力学的エネルギーが最小となるように頂点を置く:
"SpringEmbedding"は標準構造のグラフに最適である:
"EdgeWeighted"->Trueと設定すると,辺の重みが使われる:
オプション"EnergyControl"->e を使って最小化の際の系の総エネルギー量に対する制限を指定する:
"InferentialDistance"->d を使ってカットオフ距離を指定する.このカットオフ距離を超えては頂点間のインタラクションは存在しないと考えられる:
"MaxIteration"->it を使ってエネルギー最小化の試みで使用する最大反復回数を指定する:
"Multilevel"->method を使ってグラフを粗大化させる再帰的手続きに使用するメソッドを指定する:
"RandomSeed"->int を使って最初の頂点の置き方を計算する乱数生成器のシードを指定する:
オプション"Rotation"r を使ってレイアウトを回転させる:
"StepControl"->method を使ってエネルギー最小化においてどのように刻み幅が調整されるかを定義する:
"StarEmbedding" (4)
"StarEmbedding"は,星形のグラフに最適である:
"SymmetricLayeredEmbedding" (4)
SymmetricLayeredEmbeddingは,対称有向非巡回グラフに対して最も適切に機能する:
"TutteEmbedding" (2)
辺のレイアウト (3)
充填レイアウト (6)
特性と関係 (6)
GraphLayoutは一般的なグラフに使うことができる:
VertexCoordinatesはGraphLayoutの座標を無効にする:
AbsoluteOptionsを使ってレイアウトアルゴリズムで計算したVertexCoordinatesを抽出する:
関連するガイド
-
▪
- グラフのスタイル付け,ラベル付け,配置 ▪
- グラフの可視化 ▪
- グラフの特性 ▪
- グラフのアノテーション ▪
- グラフとネットワーク
履歴
2010 で導入 (8.0) | 2012 で更新 (9.0) ▪ 2014 (10.0) ▪ 2019 (12.0) ▪ 2021 (12.3) ▪ 2025 (14.2) ▪ 2025 (14.3)
テキスト
Wolfram Research (2010), GraphLayout, Wolfram言語関数, https://reference.wolfram.com/language/ref/GraphLayout.html (2025年に更新).
CMS
Wolfram Language. 2010. "GraphLayout." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/GraphLayout.html.
APA
Wolfram Language. (2010). GraphLayout. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphLayout.html
BibTeX
@misc{reference.wolfram_2025_graphlayout, author="Wolfram Research", title="{GraphLayout}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/GraphLayout.html}", note=[Accessed: 17-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_graphlayout, organization={Wolfram Research}, title={GraphLayout}, year={2025}, url={https://reference.wolfram.com/language/ref/GraphLayout.html}, note=[Accessed: 17-January-2026]}