HermitianMatrix

HermitianMatrix[hmat]

converts the Hermitian matrix hmat to a structured array.

Details and Options

  • Hermitian matrices, when represented as structured arrays, allow for a convenient specification.
  • For Hermitian matrices, it is significantly less expensive to solve eigenproblems that arise in applications.
  • A Hermitian matrix 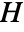satisfies H〚i,j〛=TemplateBox[{{H, 〚, {j, ,, i}, 〛}}, Conjugate].
  • The elements hij need not be numerical.
  • The inverse of a Hermitian matrix and, in general, any matrix function of a Hermitian matrix is also Hermitian.
  • For a HermitianMatrix sa, the following properties "prop" can be accessed as sa["prop"]:
  • "Matrix"Hermitian matrix, represented as a full array
    "Properties"list of supported properties
    "Structure"type of structured array
    "StructuredData"internal data stored by the structured array
    "StructuredAlgorithms"list of functions with special methods for the structured array
    "Summary"summary information, represented as a Dataset
  • Normal[HermitianMatrix[…]] gives the Hermitian matrix as an ordinary matrix.
  • HermitianMatrix[…,TargetStructure->struct] returns the Hermitian matrix in the format specified by struct. Possible settings include:
  • Automaticautomatically choose the representation returned
    "Dense"represent the matrix as a dense matrix
    "Structured"represent the matrix as a structured array
  • HermitianMatrix[…,TargetStructureAutomatic] is equivalent to HermitianMatrix[…,TargetStructure"Structured"].

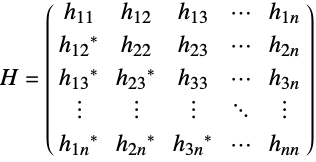
Examples

open allclose all

Basic Examples  (1)

Construct a Hermitian matrix:

Show the elements:

Normal can convert a HermitianMatrix to its ordinary representation:

Scope  (4)

Construct a Hermitian matrix from its upper-triangular entries:

Show the elements:

The matrix can also be constructed from its lower-triangular entries:

The Hilbert matrix is a Hermitian matrix:

Complex reflection matrices are both Hermitian and unitary:

HermitianMatrix objects include properties that give information about the matrix:


The "Summary" property gives a brief summary of information about the matrix:

The "StructuredAlgorithms" property lists the functions that have structured algorithms:

Options  (1)

TargetStructure  (1)

Return the Hermitian matrix as a dense matrix:

Return the Hermitian matrix as a structured array:

Applications  (3)

Matrices drawn from GaussianUnitaryMatrixDistribution are Hermitian:

Matrices drawn from GaussianSymplecticMatrixDistribution are Hermitian:

The Pauli matrices are Hermitian matrices:

A Hermitian positive-definite matrix defines an inner product by :

Verify that is positive definite:

Orthogonalize the standard basis of TemplateBox[{}, Complexes]^n to find an orthonormal basis:

Confirm that this basis is orthonormal with respect to the inner product :

Properties & Relations  (4)

The conjugate transpose of a Hermitian matrix equals the original matrix:

A real symmetric matrix is also a Hermitian matrix:

A Hermitian matrix can be represented using SymmetrizedArray or HermitianMatrix:

The two representations are equal, but support different algorithms:

SymmetrizedArray supports tensorial operations such as D, Flatten, Inner, and Outer:

HermitianMatrix supports matrix-specific operations such as KroneckerProduct:

A real Hermitian matrix can also be represented using SymmetricMatrix:

This is not true of a complex Hermitian matrix:

Wolfram Research (2024), HermitianMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/HermitianMatrix.html.

Text

Wolfram Research (2024), HermitianMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/HermitianMatrix.html.

CMS

Wolfram Language. 2024. "HermitianMatrix." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HermitianMatrix.html.

APA

Wolfram Language. (2024). HermitianMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HermitianMatrix.html

BibTeX

@misc{reference.wolfram_2024_hermitianmatrix, author="Wolfram Research", title="{HermitianMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/HermitianMatrix.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hermitianmatrix, organization={Wolfram Research}, title={HermitianMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/HermitianMatrix.html}, note=[Accessed: 21-December-2024 ]}