HermitianMatrixQ
更多信息和选项

- HermitianMatrixQ 亦称为自共轭.
- 如果 m==ConjugateTranspose[m],则矩阵 m 为埃尔米特矩阵.
- HermitianMatrixQ 可用来判定符号矩阵以及数字矩阵.
- 可使用下列选项:
-
SameTest Automatic 测试表达式是否相等的函数 Tolerance Automatic 对近似数字的容差 - 对于精确矩阵和符号矩阵,选项 SameTest->f 表示若 f[mij,mkl] 为 True,则元素 mij 和 mkl 被认为是相等的.
- 对于近似矩阵, 选项 Tolerance->t 可被用于表示所有满足 Abs[mij]≤t 的元素都被认为是零.
- 对于 Abs[mij]>t 的矩阵元素, 除了最后
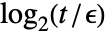 位不考虑,会对剩下的位进行相等性对比,其中,对于 MachinePrecision 矩阵,
位不考虑,会对剩下的位进行相等性对比,其中,对于 MachinePrecision 矩阵, 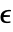 为 $MachineEpsilon,对于 Precision 为
为 $MachineEpsilon,对于 Precision 为 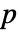 的矩阵,
的矩阵,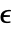 为
为 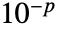 .
.
范例
打开所有单元关闭所有单元范围 (10)
基础用法 (6)
特殊矩阵 (4)
将 HermitianMatrixQ 用于稀疏矩阵:
将 HermitianMatrixQ 用于结构化矩阵:
用于 QuantityArray 结构化矩阵:
HilbertMatrix 为埃尔米特矩阵:
选项 (2)
SameTest (1)
当 ![]() 为正实数时,下述矩阵为埃尔米特矩阵,但是, HermitianMatrixQ 结果为 False:
为正实数时,下述矩阵为埃尔米特矩阵,但是, HermitianMatrixQ 结果为 False:
利用选项 SameTest 来得到正确结果:
Tolerance (1)
应用 (8)
埃尔米特矩阵的来源 (5)
利用 Table 生成埃尔米特矩阵:
SymmetrizedArray 可以生成具有对称性的矩阵(和一般数组):
使用 Normal 转换回普通矩阵:
有几个复数数据的统计度量是埃尔米特矩阵,其中包括 Covariance:
用 GaussianUnitaryMatrixDistribution 绘制的矩阵为埃尔米特矩阵:
用 GaussianSymplecticMatrixDistribution 绘制的矩阵为埃尔米特矩阵:
属性和关系 (16)
HermitianMatrixQ[x] 对于任何不是矩阵的 x 都会返回 False:
如果 m==ConjugateTranspose[m],则该矩阵为埃尔米特矩阵:
用 Diagonal 取出对角线上的元素:
使用 Symmetrize 和对称 Hermitian 计算矩阵的埃尔米特部分:
这等于 m 和 ConjugateTranspose[m] 的平均值:
任意矩阵都可被表示为一个埃尔米特矩阵与一个反埃尔米特矩阵之和:
可以用 AntihermitianMatrixQ 来判断一个矩阵是否为反埃尔米特矩阵:
对于任何埃尔米特矩阵 h,MatrixExp[I h] 都为酉矩阵:
可以用 NormalMatrixQ 来判断一个矩阵是否为正规矩阵:
用 Eigenvalues 求特征值:
埃尔米特矩阵 m 的 CharacteristicPolynomial[m,x] 有实值系数:
用 Eigenvectors 求特征向量:
使用 Det 计算行列式:
埃尔米特矩阵的实值矩阵函数是埃尔米特矩阵,包括 MatrixExp:
以及任何可使用 MatrixFunction 表示的单变量分析函数:
HermitianMatrix 可用于明确构造埃尔米特矩阵:
这满足 HermitianMatrixQ:
文本
Wolfram Research (2007),HermitianMatrixQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/HermitianMatrixQ.html (更新于 2014 年).
CMS
Wolfram 语言. 2007. "HermitianMatrixQ." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/HermitianMatrixQ.html.
APA
Wolfram 语言. (2007). HermitianMatrixQ. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HermitianMatrixQ.html 年