Hypergeometric2F1
Hypergeometric2F1[a,b,c,z]
is the hypergeometric function ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- The
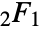 function has the series expansion
function has the series expansion ![TemplateBox[{a, b, c, z}, Hypergeometric2F1]=sum_(k=0)^(infty)TemplateBox[{a, k}, Pochhammer]TemplateBox[{b, k}, Pochhammer]/TemplateBox[{c, k}, Pochhammer] z^k/k! TemplateBox[{a, b, c, z}, Hypergeometric2F1]=sum_(k=0)^(infty)TemplateBox[{a, k}, Pochhammer]TemplateBox[{b, k}, Pochhammer]/TemplateBox[{c, k}, Pochhammer] z^k/k!](Files/Hypergeometric2F1.en/3.png) , where
, where ![TemplateBox[{a, k}, Pochhammer] TemplateBox[{a, k}, Pochhammer]](Files/Hypergeometric2F1.en/4.png) is the Pochhammer symbol.
is the Pochhammer symbol. - For certain special arguments, Hypergeometric2F1 automatically evaluates to exact values.
- Hypergeometric2F1 can be evaluated to arbitrary numerical precision.
- Hypergeometric2F1 automatically threads over lists.
- Hypergeometric2F1[a,b,c,z] has a branch cut discontinuity in the complex
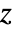 plane running from
plane running from 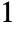 to
to 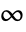 .
. - FullSimplify and FunctionExpand include transformation rules for Hypergeometric2F1.
- Hypergeometric2F1 can be used with Interval and CenteredInterval objects. »
Examples
open allclose allBasic Examples (7)
Plot ![]() over a subset of the reals:
over a subset of the reals:
Plot over a subset of the complexes:
Expand Hypergeometric2F1 in a Taylor series at the origin:
Series expansion at Infinity:
Scope (44)
Numerical Evaluation (5)
The precision of the output tracks the precision of the input:
Evaluate for complex arguments:
Evaluate Hypergeometric2F1 efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix Hypergeometric2F1 function using MatrixFunction:
Specific Values (6)
Hypergeometric2F1 automatically evaluates to simpler functions for certain parameters:
Exact value of Hypergeometric2F1 at unity:
Hypergeometric series terminates if either of the first two parameters is a negative integer:
Visualization (3)
Plot the Hypergeometric2F1 function:
Plot Hypergeometric2F1 as a function of its third parameter ![]() :
:
Function Properties (9)
Real domain of Hypergeometric2F1:
Complex domain of Hypergeometric2F1:
![]() is an analytic function on its real domain:
is an analytic function on its real domain:
It is neither analytic nor meromorphic in the complex plane:
![]() is non-decreasing on its real domain:
is non-decreasing on its real domain:
![]() is non-negative on its real domain:
is non-negative on its real domain:
![]() has both singularity and discontinuity for
has both singularity and discontinuity for ![]() :
:
TraditionalForm formatting:
Differentiation (3)
Integration (3)
Indefinite integral of Hypergeometric2F1:
Definite integral of Hypergeometric2F1:
Series Expansions (6)
Taylor expansion for Hypergeometric2F1:
Plot the first three approximations for ![]() around
around ![]() :
:
General term in the series expansion of Hypergeometric2F1:
Expand Hypergeometric2F1 in a series near ![]() :
:
Expand Hypergeometric2F1 in a series around ![]() :
:
Give the result for an arbitrary symbolic direction ![]() :
:
Apply Hypergeometric2F1 to a power series:
Integral Transforms (2)
Function Representations (5)
Relation to the JacobiP polynomial:
Hypergeometric2F1 can be represented as a DifferentialRoot:
Hypergeometric2F1 can be represented in terms of MeijerG:
TraditionalForm formatting:
Applications (3)
An expression for the force acting on an electric point charge ![]() outside a neutral dielectric sphere of radius
outside a neutral dielectric sphere of radius ![]() :
:
The limit of infinite dielectric constant, corresponding to an uncharged insulated conducting sphere:
An approximation for the force at a large distance from the sphere:
Two players roll dice. If the total of both numbers is less than 10, the second player is paid 4 cents; otherwise, the first player is paid 9 cents. Is the game fair? Compute the probability that the first player gets paid:
The game is not fair, since mean scores per game are not equal:
Find the probability that after n games the player at the disadvantage scores more:
The probability exhibits oscillations:
The maximum probability is attained at ![]() :
:
Riemann's differential equation with three regular singularities at ![]() and exponent parameters
and exponent parameters ![]() , subject to the constraint
, subject to the constraint ![]() :
:
Construct two linearly independent solutions in terms of Hypergeometric2F1:
Properties & Relations (2)
Use FunctionExpand to expand Hypergeometric2F1 into other functions:
Find limits of Hypergeometric2F1 from below and above the branch cut:
Possible Issues (1)
![]() is equivalent to
is equivalent to ![]() for generic
for generic ![]() :
:
However, if ![]() is a negative integer, Hypergeometric2F1 returns a polynomial:
is a negative integer, Hypergeometric2F1 returns a polynomial:
Text
Wolfram Research (1988), Hypergeometric2F1, Wolfram Language function, https://reference.wolfram.com/language/ref/Hypergeometric2F1.html (updated 2022).
CMS
Wolfram Language. 1988. "Hypergeometric2F1." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Hypergeometric2F1.html.
APA
Wolfram Language. (1988). Hypergeometric2F1. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Hypergeometric2F1.html