Hypergeometric2F1[a,b,c,z]
超幾何関数![]() である.
である.




Hypergeometric2F1
Hypergeometric2F1[a,b,c,z]
超幾何関数![]() である.
である.
詳細

- 記号操作・数値操作の両方に適した数学関数である.
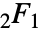 関数は級数展開
関数は級数展開 ![TemplateBox[{a, b, c, z}, Hypergeometric2F1]=sum_(k=0)^(infty)TemplateBox[{a, k}, Pochhammer]TemplateBox[{b, k}, Pochhammer]/TemplateBox[{c, k}, Pochhammer] z^k/k! TemplateBox[{a, b, c, z}, Hypergeometric2F1]=sum_(k=0)^(infty)TemplateBox[{a, k}, Pochhammer]TemplateBox[{b, k}, Pochhammer]/TemplateBox[{c, k}, Pochhammer] z^k/k!](Files/Hypergeometric2F1.ja/3.png) を持つ.ここで,
を持つ.ここで,![TemplateBox[{a, k}, Pochhammer] TemplateBox[{a, k}, Pochhammer]](Files/Hypergeometric2F1.ja/4.png) はPochhammer記号である.
はPochhammer記号である.- 特別な引数の場合,Hypergeometric2F1は,自動的に厳密値を計算する.
- Hypergeometric2F1は任意の数値精度で評価できる.
- Hypergeometric2F1逆ヤコビ楕円関数は楕円積分に関係する.
- Hypergeometric2F1[a,b,c,z]は,複素
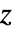 平面上,
平面上,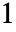 〜
〜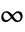 の範囲で不連続な分枝切断線を持つ.
の範囲で不連続な分枝切断線を持つ. - FullSimplifyおよびFunctionExpandは,Hypergeometric2F1の変換規則を含む.
- Hypergeometric2F1はIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
例題
すべて開く すべて閉じる例 (7)
テイラー(Taylor)級数におけるHypergeometric2F1を原点で展開する:
Infinityにおける級数展開:
スコープ (44)
数値評価 (5)
Hypergeometric2F1を高精度で効率よく評価する:
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する:
Aroundを使って平均的な場合の統計区間を計算することもできる:
MatrixFunctionを使って行列のHypergeometric2F1関数を計算することもできる:
特定の値 (6)
Hypergeometric2F1は,ある種の引数については評価すると自動的により簡単な関数になる:
単位元におけるHypergeometric2F1の厳密値:
可視化 (3)
関数の特性 (9)
積分 (3)
級数展開 (6)
Hypergeometric2F1のテイラー展開:
Hypergeometric2F1の級数展開における一般項:
![]() の近くにおけるHypergeometric2F1の級数展開:
の近くにおけるHypergeometric2F1の級数展開:
![]() の近くにおけるHypergeometric2F1の級数展開:
の近くにおけるHypergeometric2F1の級数展開:
Hypergeometric2F1をベキ級数に適用する:
積分変換 (2)
関数表現 (5)
JacobiP多項式との関係:
Hypergeometric2F1はDifferentialRootとして表現できる:
Hypergeometric2F1はMeijerGによって表現できる:
TraditionalFormによる表示:
アプリケーション (3)
半径 ![]() の中性誘電体球の外側の点電荷
の中性誘電体球の外側の点電荷 ![]() 上で作用している力の式:
上で作用している力の式:
荷電されていない絶縁導電球に対応する無限大の誘電定数の極限:
2人のプレーヤーがサイコロを振っている.両者の数の合計が10未満なら2番目のプレーヤーに4セントが支払われる.それ以外の場合は最初のプレーヤーに9セントが支払われる.このゲームは公平だろうか.最初のプレーヤーが支払いを受ける確率を計算する:
ゲームあたりの平均スコアが等しくないのでこのゲームは公平ではない:
n ゲーム後に不利なプレーヤーの方がスコアがよくなる確率を求める:
3つの確定特異点 ![]() と指数パラメータ
と指数パラメータ ![]() を持ち制約条件t
を持ち制約条件t ![]() に従うリーマンの微分方程式:
に従うリーマンの微分方程式:
Hypergeometric2F1によって2つの線形独立解を構築する:
特性と関係 (2)
考えられる問題 (1)
しかし,![]() が負の整数である場合は,Hypergeometric2F1は多項式を返す:
が負の整数である場合は,Hypergeometric2F1は多項式を返す:
テクニカルノート
-
▪
- 特殊関数
関連するガイド
-
▪
- 超幾何関数 ▪
- 特殊関数 ▪
- 数学関数 ▪
- 分離可能な座標系の関数 ▪
- 量子力学で使用される関数
履歴
1988 で導入 (1.0) | 1999 で更新 (4.0) ▪ 2021 (13.0) ▪ 2022 (13.1)
テキスト
Wolfram Research (1988), Hypergeometric2F1, Wolfram言語関数, https://reference.wolfram.com/language/ref/Hypergeometric2F1.html (2022年に更新).
CMS
Wolfram Language. 1988. "Hypergeometric2F1." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Hypergeometric2F1.html.
APA
Wolfram Language. (1988). Hypergeometric2F1. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Hypergeometric2F1.html
BibTeX
@misc{reference.wolfram_2025_hypergeometric2f1, author="Wolfram Research", title="{Hypergeometric2F1}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/Hypergeometric2F1.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_hypergeometric2f1, organization={Wolfram Research}, title={Hypergeometric2F1}, year={2022}, url={https://reference.wolfram.com/language/ref/Hypergeometric2F1.html}, note=[Accessed: 09-March-2026]}