InverseWaveletTransform

InverseWaveletTransform[dwd]

DiscreteWaveletDataオブジェクト dwd の逆ウェーブレット変換を与える．

InverseWaveletTransform[dwd,wave]

ウェーブレット wave を使って逆変換を与える．

InverseWaveletTransform[dwd,wave,wind]

wind で指定されたウェーブレット係数から逆変換を与える．

詳細とオプション

  • InverseWaveletTransformはDiscreteWaveletTransform等のような離散前方変換の逆変換を計算する．
  • 使用可能なウェーブレット wave は前方ウェーブレット変換で使用できるものと同じである．
  • デフォルトの wave はAutomaticで，dwd["Wavelet"]とみなされる．
  • wind の可能な指定値はDiscreteWaveletDataで使われるものと同じである．
  • デフォルトの wind はAutomaticで，dwd["BasisIndex"]とみなされる．
  • InverseWaveletTransform[dwd,wave,wind]は wind が指定したウェーブレット係数だけを使って逆変換を計算する．他の係数は0に設定される．
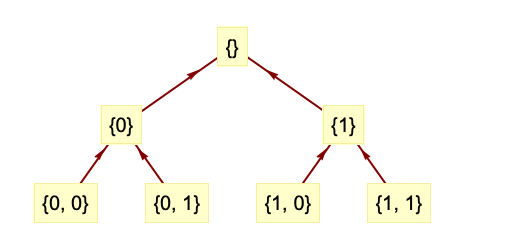
  • 逆変換は，ウェーブレット指標{w1,…,wn-1,wn}を持つ係数からウェーブレット指標{w1,…,wn-1}を持つ係数を計算することで再帰的に働く．
  • 明示的な wind 指定には整合性がなければならない．含まれている各{w1,…,wn}に k<n の{w1,…,wk}が含まれていなければその wind 指定には整合性がある．
  • InverseWaveletTransform[dwd,wave,r]を使って，ウェーブレット木の下から r レベルまでの逆変換を行うことができる．
  • デフォルトレベル r は dwd における細分化レベルの数 n で与えられる．r<n では，細分化レベルが n-r の新しいDiscreteWaveletDataオブジェクトが返される．

例題

すべて開くすべて閉じる

例  (3)

離散ウェーブレット変換を行う：

逆変換でもとのデータを復元する：

修正されたウェーブレット画像係数を表すDiscreteWaveletData：

逆変換でフィルターされた画像が与えられる：

音声信号を表すDiscreteWaveletData：

細分化レベル5の係数だけを使った逆変換：

スコープ  (14)

基本的な用法  (8)

任意の離散前方変換からDiscreteWaveletDataへの逆ウェーブレット変換：

前方変換から直接得られたデータの逆変換は厳密である：

修正されたDiscreteWaveletDataの逆ウェーブレット変換：

逆変換は修正ウェーブレット係数から計算される：

指定のウェーブレット係数だけを使った逆ウェーブレット変換：

詳細化係数{0,1}のみの逆変換：

{0,_}にマッチするすべてのウェーブレット係数を逆変換しその他の係数は0に設定する：

明示的に構築されたDiscreteWaveletDataオブジェクトの逆変換：

ウェーブレット変換のタイプは指定された係数の形式から推察される：

指定されていない係数は0とみなされる：

逆変換に使用する別のウェーブレットを指定する：

デフォルトで，前方変換に使われるウェーブレットが選ばれる：

配列データの逆変換は同じ次元の配列である：

画像データの逆変換はImageオブジェクトとして与えられる：

画像はもとのデータと同じ次元でカラーチャンネルの数も同じである：

サウンドデータの逆変換はSoundで与えられる：

サウンドはもとのサウンドと同じ長さでサンプリングレートやチャンネル数も等しい：

再構築の基底  (6)

使用可能なウェーブレットの部分集合が逆変換に使用される：

dwd["BasisIndex"]は逆変換がデフォルトで使用する係数を与える：

dwd["TreeView"]を使ってデフォルト基底をハイライトしたすべての係数のツリープロットを得る：

係数のデフォルト基底を使って逆変換を計算する：

特定の基底を使って逆変換を計算する：

基底の特定の部分集合を使い，他の係数は0とみなす：

一つの係数の逆変換を計算する：

すべての非パケットDiscreteWaveletDataに対し標準基底がデフォルトとして選ばれる：

基底には詳細化係数{…,1}と最後の粗い係数{…,0}が含まれる：

パケット変換データのデフォルト基底は最高の細分化レベルの係数を使う：

パケット変換データについては，WaveletBestBasisを使ってウェーブレット基底を変更することができる：

係数の情報エントロピーを最小化する基底を選ぶ：

特定の基底を選ぶ：

すべての係数のツリープロットで各基底をハイライトする：

パケット変換から直接得られたデータの逆変換は基底に依存しない：

いくつかの異なる完全ウェーブレット基底指定について逆変換を比較する：

変更されたウェーブレットデータの逆変換は選ばれた基底に依存する場合がある：

一般化と拡張  (2)

部分逆ウェーブレット変換：

細分化レベルが1低いDiscreteWaveletDataを得る：

個の最低レベルでの細分化で反転した後で残ったウェーブレット係数を可視化する：

InverseWaveletTransform[dwd]は細分化のすべてのレベルを反転させることに等しい：

複素ウェーブレット係数の逆変換：

InverseWaveletTransformは厳密な逆変換を与える：

アプリケーション  (8)

ウェーブレット合成  (2)

細分化レベル の詳細化係数{0,…,1}のノイズからなる離散ウェーブレットデータ：

逆ウェーブレット変換を使い1つの特定のスケールでノイズを合成する：

垂直詳細化係数{2,2} のみのノイズからなる静的ウェーブレット行列データ：

逆ウェーブレット変換を使ってノイズのあるデータを合成する：

異なるウェーブレット係数のノイズを使うと異なる種類のノイズのあるデータが合成される：

逆離散ウェーブレット変換  (3)

に等しい最初の粗い係数を持つ離散ウェーブレット変換データ：

さまざまな粗い係数の逆変換を可視化する：

に等しい最初の詳細化係数を持つ離散ウェーブレット変換データ：

異なる詳細関係数の逆変換を可視化する：

ウェーブレット係数 を持つ離散ウェーブレットパケット変換データ：

各係数の逆変換を別々に可視化する：

逆変換集合は信号空間の基底を形成する：

逆静的ウェーブレット変換  (3)

に等しい最初の粗い係数を持つ静的ウェーブレット変換データ：

さまざまな粗い係数の逆変換を可視化する：

に等しい最初の詳細化係数を持つ静的ウェーブレット変換データ：

異なる詳細化係数の逆変換を可視化する：

ウェーブレット係数が の静的ウェーブレットパケット変換データ：

各係数の各要素 の逆変換を別々に可視化する：

16の逆変換集合は信号空間に及ぶ：

特性と関係  (7)

InverseWaveletTransformは対角ウェーブレットを使った変換の厳密な逆変換である：

対角HaarWaveletを使う：

逆変換はShannonWaveletのような非対角ウェーブレット族については厳密ではない：

デフォルトで，dwd["BasisIndex"]の係数が逆変換に使われる：

他のすべての係数を0にする：

デフォルト基底を使った逆変換には影響がない：

InverseWaveletTransform[…,…,wind]は事実上他のウェーブレット係数を0に設定する：

他のウェーブレット係数を明示的に0に設定する：

InverseWaveletTransform[…,…,wind]は係数 wind から逆変換を計算する：

dwd[wind,"Inverse"]は個々の係数の逆変換を別々に計算する：

合計はInverseWaveletTransformと同じ結果を与える：

ListLinePlotを使って個々のベクトル係数の逆変換をプロットする：

dwd[wind,{"Inverse","ListPlot"}]は各逆変換の簡単なリストプロットを与える：

WaveletListPlot[dwd,wind,Method->"Inverse"->True]は逆変換も一緒にプロットする：

MatrixPlotを使って個々の行列係数の逆変換をプロットする：

dwd[wind,{"Inverse","MatrixPlot"}]は各逆変換の簡単な行列プロットを与える：

画像データからの個々の係数の逆変換はImageオブジェクトとして与えられる：

考えられる問題  (1)

r<n について{a1,…,an}と{a1,…,ar}の両方が含まれている場合，この wind 指定には整合性がない：

逆変換は{1,0}から{1}を計算するので，この指定には整合性がない：

整合性のある wind 指定を使う：

Wolfram Research (2010), InverseWaveletTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseWaveletTransform.html.

テキスト

Wolfram Research (2010), InverseWaveletTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseWaveletTransform.html.

CMS

Wolfram Language. 2010. "InverseWaveletTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseWaveletTransform.html.

APA

Wolfram Language. (2010). InverseWaveletTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseWaveletTransform.html

BibTeX

@misc{reference.wolfram_2024_inversewavelettransform, author="Wolfram Research", title="{InverseWaveletTransform}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/InverseWaveletTransform.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inversewavelettransform, organization={Wolfram Research}, title={InverseWaveletTransform}, year={2010}, url={https://reference.wolfram.com/language/ref/InverseWaveletTransform.html}, note=[Accessed: 17-November-2024 ]}