InverseWaveletTransform
给出一个 DiscreteWaveletData 对象 dwd 的逆小波变换.
InverseWaveletTransform[dwd,wave]
给出使用小波 wave 的逆变换.
InverseWaveletTransform[dwd,wave,wind]
给出来自由 wind 指定的小波系数的逆变换.
更多信息和选项

- InverseWaveletTransform 计算正向离散变换如 DiscreteWaveletTransform 等的逆变换.
- 可能的小波 wave 与正向小波变换的相同.
- 默认的 wave 是 Automatic,采用 dwd["Wavelet"].
- wind 的可能指定与 DiscreteWaveletData 所用的相同.
- 默认的 wind 是 Automatic,采用 dwd["BasisIndex"].
- InverseWaveletTransform[dwd,wave,wind] 只使用由 wind 指定的小波系数计算逆变换;其他系数设置为零.
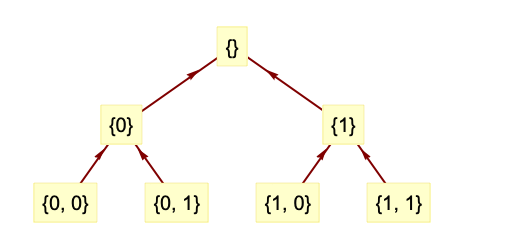
- 逆变换通过计算来自具有小波指标 {w1,…,wn-1,wn} 的系数的小波指标 {w1,…,wn-1} 系数递归地起作用.
- 一个明确的 wind 指定必须是一致的. 一个 wind 指定是一致的,如果对于每个包括的 {w1,…,wn},没有包含 k<n 的 {w1,…,wk}.
- InverseWaveletTransform[dwd,wave,r] 可以用来对小波树的 r 个最低层进行逆变换.
- 默认层 r 由 dwd 中精细度 n 的数目给出. 在 r<n 下,返回具有 n-r 精细度的一个新的 DiscreteWaveletData 对象.
范例
打开所有单元关闭所有单元基本范例 (3)
DiscreteWaveletData 表示修正后的小波图像系数:
表示一个音频信号的 DiscreteWaveletData:
范围 (14)
基本用途 (8)
来自任意正向离散变换的逆小波变换 DiscreteWaveletData:
逆小波变换修改了 DiscreteWaveletData:
逆变换使用所有匹配 {0,_} 的小波系数,并且把其它系数设置为零:
逆变换明确构建 DiscreteWaveletData 对象:
对于图像数据,逆变换作为一个 Image 对象给出:
对于声音数据,逆变换作为一个 Sound 对象给出:
重构基 (6)
dwd["BasisIndex"] 给出默认在逆变换中所用的系数:
使用 dwd["TreeView"] 来获取具有突出显示的默认基的所有系数组成的树图:
选择标准基作为所有非包 DiscreteWaveletData 的默认值:
对于包变换数据,小波基可使用 WaveletBestBasis 改变:
推广和延伸 (2)
获取少一个精细度的 DiscreteWaveletData:
InverseWaveletTransform[dwd] 等价于对所有精细度取逆:
InverseWaveletTransform 给出精确的逆变换:
应用 (8)
小波合成 (2)
逆离散小波变换 (3)
属性和关系 (7)
InverseWaveletTransform 是使用正交小波的变换的精确逆变换:
使用正交 HaarWavelet:
对于非正交小波族,如 ShannonWavelet,逆变换是不精确的:
默认情况下,dwd["BasisIndex"] 中的系数被用于逆变换中:
InverseWaveletTransform[…,…,wind] 实际上把其它小波系数设置为零:
InverseWaveletTransform[…,…,wind] 从系数 wind 计算逆变换:
dwd[wind,"Inverse"] 分别计算每个系数的逆变换:
总和给出与 InverseWaveletTransform 相同的结果:
使用 ListLinePlot 来绘制单个向量系数的逆变换:
dwd[wind,{"Inverse","ListPlot"}] 给出每个逆变换的简单列表图线:
WaveletListPlot[dwd,wind,Method->"Inverse"->True] 把逆变换绘制在一起:
使用 MatrixPlot 来绘制单个矩阵系数的逆变换:
dwd[wind,{"Inverse","MatrixPlot"}] 给出每个逆变换的简单矩阵图表:
图像数据的单个系数的逆变换由 Image 对象给出:
文本
Wolfram Research (2010),InverseWaveletTransform,Wolfram 语言函数,https://reference.wolfram.com/language/ref/InverseWaveletTransform.html.
CMS
Wolfram 语言. 2010. "InverseWaveletTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/InverseWaveletTransform.html.
APA
Wolfram 语言. (2010). InverseWaveletTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/InverseWaveletTransform.html 年