InverseZTransform[expr,z,n]
expr の逆Z変換を与える.
InverseZTransform[expr,{z1,…,zm},{n1,…,nm}]
expr の多重逆Z変換を与える


InverseZTransform
InverseZTransform[expr,z,n]
expr の逆Z変換を与える.
InverseZTransform[expr,{z1,…,zm},{n1,…,nm}]
expr の多重逆Z変換を与える
詳細とオプション
- 関数
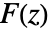 の逆Z変換は,周辺積分
の逆Z変換は,周辺積分 で与えられる.
で与えられる. - 多重逆Z変換は
 で与えられる.
で与えられる. - 使用可能なオプション
-
Assumptions $Assumptions パラメータについての仮定 Method Automatic 使用するメソッド - TraditionalFormでは,InverseZTransformは
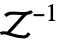 を使って出力される.
を使って出力される.
例題
すべて開く すべて閉じるオプション (1)
Assumptions (1)
この変換は p の範囲についてのなんらかの制約条件なしには評価しない:
Assumptionsを使って p の範囲を制限する:
アプリケーション (3)
特性と関係 (6)
テクニカルノート
関連リンク
履歴
1999 で導入 (4.0) | 2008 で更新 (7.0)
テキスト
Wolfram Research (1999), InverseZTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/InverseZTransform.html (2008年に更新).
CMS
Wolfram Language. 1999. "InverseZTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/InverseZTransform.html.
APA
Wolfram Language. (1999). InverseZTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseZTransform.html
BibTeX
@misc{reference.wolfram_2025_inverseztransform, author="Wolfram Research", title="{InverseZTransform}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/InverseZTransform.html}", note=[Accessed: 07-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_inverseztransform, organization={Wolfram Research}, title={InverseZTransform}, year={2008}, url={https://reference.wolfram.com/language/ref/InverseZTransform.html}, note=[Accessed: 07-January-2026]}