InverseZTransform[expr,z,n]
给出 expr 的 Z 反变换.
InverseZTransform[expr,{z1,…,zm},{n1,…,nm}]
给出 expr 的多维 Z 反变换.


InverseZTransform
InverseZTransform[expr,z,n]
给出 expr 的 Z 反变换.
InverseZTransform[expr,{z1,…,zm},{n1,…,nm}]
给出 expr 的多维 Z 反变换.
更多信息和选项
- 一个函数
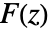 的 Z 反变换定义为等高线积分
的 Z 反变换定义为等高线积分 .
. - 多维 Z 反变换定义为
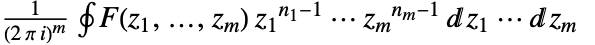 .
. - 可以给出下列选项:
-
Assumptions $Assumptions 关于参数的假设 Method Automatic 使用的方法 - 在 TraditionalForm 中,InverseZTransform 使用
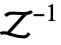 输出.
输出.
范例
打开所有单元 关闭所有单元选项 (1)
Assumptions (1)
用 Assumptions 限制 p 的范围:
应用 (3)
属性和关系 (6)
技术笔记
相关链接
历史
1999年引入 (4.0) | 在以下年份被更新:2008 (7.0)
文本
Wolfram Research (1999),InverseZTransform,Wolfram 语言函数,https://reference.wolfram.com/language/ref/InverseZTransform.html (更新于 2008 年).
CMS
Wolfram 语言. 1999. "InverseZTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2008. https://reference.wolfram.com/language/ref/InverseZTransform.html.
APA
Wolfram 语言. (1999). InverseZTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/InverseZTransform.html 年
BibTeX
@misc{reference.wolfram_2025_inverseztransform, author="Wolfram Research", title="{InverseZTransform}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/InverseZTransform.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_inverseztransform, organization={Wolfram Research}, title={InverseZTransform}, year={2008}, url={https://reference.wolfram.com/language/ref/InverseZTransform.html}, note=[Accessed: 05-February-2026]}