ItoProcess

ItoProcess[{a,b},x,t]

represents an Ito process , where .

ItoProcess[{a,b,c},x,t]

represents an Ito process , where .

ItoProcess[…,{x,x0},{t,t0}]

uses initial condition .

ItoProcess[…,…,…,Σ]

uses a Wiener process , with covariance Σ.

ItoProcess[proc]

converts proc to a standard Ito process whenever possible.

ItoProcess[sdeqns,expr,x,t,wdproc]

represents an Ito process specified by a stochastic differential equation sdeqns, output expression expr, with state x and time t, driven by w following the process dproc.

Details and Options

  • ItoProcess is also known as Ito diffusion or stochastic differential equation (SDE).
  • ItoProcess is a continuous-time and continuous-state random process.
  • If the drift a is an 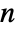-dimensional vector and the diffusion b an 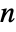×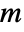-dimensional matrix, the process is 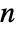-dimensional and driven by an 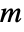-dimensional WienerProcess.
  • Common specifications for coefficients a and b include:
  • a scalar, b scalar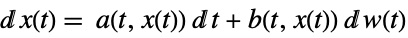
    a scalar, b vector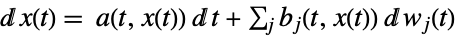
    a vector, b vector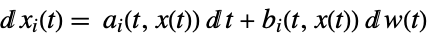
    a vector, b matrix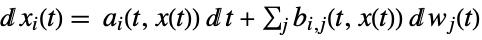
  • A stochastic differential equation 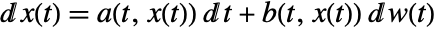is sometimes written as an integral equation .
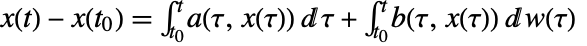  • The default initial time t0 is taken to be zero, and the default initial state x0 is zero.
  • The default covariance Σ is the identity matrix.
  • For a general covariance Σ, ItoProcess canonicalizes the process by converting the diffusion matrix b to b.Σ1/2, with Σ1/2 the lower Cholesky factor of Σ when possible.
  • A standard Ito process has output , consisting of a subset of differential states .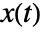
  • Processes proc that can be converted to standard ItoProcess form include OrnsteinUhlenbeckProcess, GeometricBrownianMotionProcess, StratonovichProcess, and ItoProcess.
  • Converting an ItoProcess to standard form automatically makes use of Ito's lemma.
  • The stochastic differential equations in sdeqns can be of the form 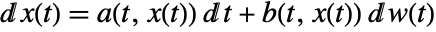, where 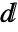is \[DifferentialD], which can be input using dd. The differentials 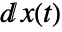and 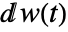are taken to be Ito differentials.
  • The output expression expr can be any expression involving x[t] and t.
  • The driving process dproc can be any process that can be converted to a standard Ito process.
  • Method settings in RandomFunction specific to ItoProcess include:
  • "EulerMaruyama"Euler–Maruyama (order 1/2, default)
    "KloedenPlatenSchurz"Kloeden–Platen–Schurz (order 3/2)
    "Milstein"Milstein (order 1)
    "StochasticRungeKutta"3‐stage Rossler SRK scheme (order 1)
    "StochasticRungeKuttaScalarNoise"3‐stage Rossler SRK scheme for scalar noise (order 3/2)
  • ItoProcess can be used with such functions as RandomFunction, CovarianceFunction, PDF, and Expectation.

Examples

open allclose all

Basic Examples  (1)

Define a process by its stochastic differential equation:

Simulate the process:

Compute mean function:

Compute covariance function:

Scope  (16)

Basic Uses  (9)

Define a Wiener process with drift and diffusion from the stochastic differential equation (SDE) :

Directly convert from the parametric process:

Define a process , where :

Use differential notation to define the same process:

Define a vector process with output :

Using differential notation:

Define a vector process , where :

Using differential notation:

Define a vector process where :

Using differential notation:

Define a process driven by two correlated Wiener processes: »

The canonicalized process has diffusion matrix equal to , with the diffusion matrix before canonicalization:

Define a scalar process corresponding to the SDE :

Define vector process and corresponding to the SDE and :

Define a process corresponding to the 2D correlated Wiener process:

Define vector process driven by correlated 2D Wiener process:

Special Ito Processes  (5)

An Ito process corresponding to the WienerProcess:

An Ito process corresponding to the GeometricBrownianMotionProcess:

An Ito process corresponding to the BrownianBridgeProcess:

An Ito process corresponding to the OrnsteinUhlenbeckProcess:

An Ito process corresponding to the CoxIngersollRossProcess:

Process Slice Properties  (2)

Define Jacobi diffusion process:

Compute low-order cumulants of time‐slice distribution:

Find the limit of infinite time horizon:

Compare with cumulants of the uniform distribution:

Define a vector process given by a system of linear SDEs:

Find the probability density function of the time‐slice distribution:

Compute cross‐covariance of and :

Infinite time horizon limit exists only if :

Applications  (5)

Computing Properties  (3)

Compute cross-covariance of the Ornstein–Uhlenbeck process and its underlying Wiener process :

Compute moments of the process , where is the standard Wiener process:

Vector Ito process driven by scalar noise (1D oscillator driven by white noise):

Simulate process paths:

Compute mean and variance functions:

Plot mean function and the standard deviation band, together with generated paths:

Martingales  (1)

Determine values of and for which the process is a martingale, where is the standard Wiener process:

Convert to the standard form:

Zero drift coefficient of the standard form is a necessary condition for to be a martingale:

Modeling  (1)

The Gompertz curve is typically used in the modeling of a growth process, such as tumor growth. By assuming Gaussian noise in the logarithm of the growth process, you can write the model as a stochastic differential equation:

Mean of the process is the usual Gompertz curve:

Slice distribution of the process at time obeys LogNormalDistribution:

Simulate the process with , and from to :

Visualize the sampled path:

Generate a thousand samples with the same conditions, then visualize the paths and slice data at :

Properties & Relations  (2)

Convert StratonovichProcess to ItoProcess:

Convert back:

Transformed Wiener processes are related to ItoProcess:

Mean and variance functions agree:

Possible Issues  (2)

ItoProcess does not support random initial conditions, so cannot be represented:

But it supports processes with fixed initial condition:

Initial time of the driven process needs to match with ItoProcess:

With matching initial time, this can be represented:

Wolfram Research (2012), ItoProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/ItoProcess.html (updated 2016).

Text

Wolfram Research (2012), ItoProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/ItoProcess.html (updated 2016).

CMS

Wolfram Language. 2012. "ItoProcess." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ItoProcess.html.

APA

Wolfram Language. (2012). ItoProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ItoProcess.html

BibTeX

@misc{reference.wolfram_2021_itoprocess, author="Wolfram Research", title="{ItoProcess}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ItoProcess.html}", note=[Accessed: 24-May-2022 ]}

BibLaTeX

@online{reference.wolfram_2021_itoprocess, organization={Wolfram Research}, title={ItoProcess}, year={2016}, url={https://reference.wolfram.com/language/ref/ItoProcess.html}, note=[Accessed: 24-May-2022 ]}