LeveneTest
LeveneTest[data]
检验 data 的方差是否为1.
LeveneTest[{data1,data2,…}]
检验 data1、data2, … 的方差是否相等.
LeveneTest[dspec,![]() ]
]
检验一个离散量数与 ![]() 的关系.
的关系.
LeveneTest[dspec,![]() ,"property"]
,"property"]
返回 "property" 的值.
更多信息和选项



- LeveneTest 检验零假设
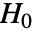 与备择假设
与备择假设 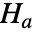 :
: -
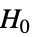
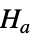
data 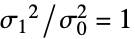
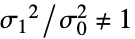
{data1,data2} 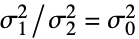
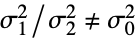
{data1,data2,…} 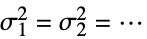
不是都相等 - 其中 σi2 是 datai 的总体方差.
- 默认情况下,返回一个概率值或者
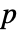 值.
值. - 一个较小的
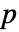 值表明
值表明 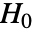 不可能为真.
不可能为真. - dspec 中的 data 必须是单变量 {x1,x2,…}.
- 参数
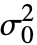 可以是任意正实数. 如果没有指定,
可以是任意正实数. 如果没有指定,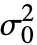 的默认值为 1,如果 dspec 中的组数大于 2,则将其忽略.
的默认值为 1,如果 dspec 中的组数大于 2,则将其忽略. - LeveneTest 假设数据服从正态分布,并且对于具有两个样本的情况,相比 FisherRatioTest,它对于该假设不灵敏得多.
- LeveneTest[data,
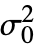 ,"HypothesisTestData"] 返回 HypothesisTestData 目标 htd,可以用 htd["property"] 形式来提取额外的检验结果和属性.
,"HypothesisTestData"] 返回 HypothesisTestData 目标 htd,可以用 htd["property"] 形式来提取额外的检验结果和属性. - LeveneTest[data,
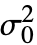 ,"property"] 可以用于直接给出 "property" 值.
,"property"] 可以用于直接给出 "property" 值. - 与检验结果的报告相关的属性包括:
-
"DegreesOfFreedom" 检验中所用的自由度 "PValue" 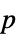 值组成的列表
值组成的列表"PValueTable" 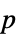 值组成的格式化表格
值组成的格式化表格"ShortTestConclusion" 检验结论的简短描述 "TestConclusion" 检验结论的描述 "TestData" 检验统计量和 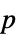 值对组成的列表
值对组成的列表"TestDataTable" 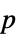 值和检验统计量组成的格式化表格
值和检验统计量组成的格式化表格"TestStatistic" 检验统计量组成的列表 "TestStatisticTable" 检验统计量组成的格式化表格 - 当给定样本数
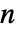 时,LeveneTest 等价于 FisherRatioTest.
时,LeveneTest 等价于 FisherRatioTest. - 对于有
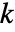 个样本的情况 {data1,data2,…,datak},其中 datai={xi,1,xi,2,…,xi,ni},检验的统计量为
个样本的情况 {data1,data2,…,datak},其中 datai={xi,1,xi,2,…,xi,ni},检验的统计量为 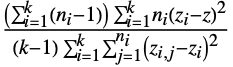 ,其中 zi,j=Abs[xi,j-Mean[datai]],zi=Mean[{zi,1,zi,2,…,zi,ni}],z=Mean[{z1,z2,…,zk}]. 在零假设
,其中 zi,j=Abs[xi,j-Mean[datai]],zi=Mean[{zi,1,zi,2,…,zi,ni}],z=Mean[{z1,z2,…,zk}]. 在零假设 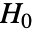 条件下,假定检验统计量服从 FRatioDistribution[k-1,
条件下,假定检验统计量服从 FRatioDistribution[k-1,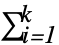 (ni-1)].
(ni-1)]. - 可以使用以下选项:
-
AlternativeHypothesis "Unequal" 备择假定的不等性 SignificanceLevel 0.05 用于诊断和报告的分界点 VerifyTestAssumptions Automatic 设置要运行哪个诊断检验 - 对于 LeveneTest,选择一个临界值
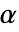 ,使得只有当
,使得只有当 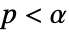 时,拒绝
时,拒绝 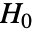 . 用于"TestConclusion" 和 "ShortTestConclusion" 属性的
. 用于"TestConclusion" 和 "ShortTestConclusion" 属性的 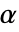 值由 SignificanceLevel 选项控制.
值由 SignificanceLevel 选项控制. 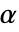 值也用于包括正态性和对称性检验的假设的诊断检验中. 默认情况下,
值也用于包括正态性和对称性检验的假设的诊断检验中. 默认情况下,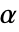 设置为 0.05.
设置为 0.05. - 在 LeveneTest 中,VerifyTestAssumptions 的已命名设置包括:
-
"Normality" 验证所有数据都服从正态分布
范例
打开所有单元关闭所有单元基本范例 (2)
范围 (10)
检验 (8)
创建一个 HypothesisTestData 对象,以进行重复属性提取:
从 HypothesisTestData 提取某些属性:
选项 (8)
AlternativeHypothesis (3)
SignificanceLevel (2)
应用 (1)
属性和关系 (8)
当只有一个数据集时,Levene 检验等价于 FisherRatioTest:
给定长度为 ![]() 的单个数据集,在
的单个数据集,在 ![]() 之下,检验统计量服从 ChiSquareDistribution[n-1]:
之下,检验统计量服从 ChiSquareDistribution[n-1]:
给定长度为 ![]() 和
和 ![]() 的两个数据集,在
的两个数据集,在 ![]() 之下,检验统计量服从 FRatioDistribution[1,n+m-2]:
之下,检验统计量服从 FRatioDistribution[1,n+m-2]:
比起 FisherRatioTest, Levene 检验对正态性假设较不敏感:
Fisher-Ratio 检验倾向于低估 ![]() 值,因而会产生更多的第一类错误:
值,因而会产生更多的第一类错误:
当输入为 TimeSeries 时,Levene 检验只能用于数值:
当输入为 TemporalData 时,Levene 检验可用于所有的值:
可能存在的问题 (3)
Levene 检验假定数据从 NormalDistribution 中抽取:
对非正态数据使用 ConoverTest 或者 SiegelTukeyTest:
当组数超过两个时,Levene 检验只允许对备择假设进行双侧检验:
文本
Wolfram Research (2010),LeveneTest,Wolfram 语言函数,https://reference.wolfram.com/language/ref/LeveneTest.html (更新于 2017 年).
CMS
Wolfram 语言. 2010. "LeveneTest." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/LeveneTest.html.
APA
Wolfram 语言. (2010). LeveneTest. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LeveneTest.html 年