LocationEquivalenceTest[{data1,data2,…}]
dataiの平均あるいは中央値が等しいかどうかの検定を行う.
LocationEquivalenceTest[{data1,…},"property"]
"property"の値を返す.


LocationEquivalenceTest
LocationEquivalenceTest[{data1,data2,…}]
dataiの平均あるいは中央値が等しいかどうかの検定を行う.
LocationEquivalenceTest[{data1,…},"property"]
"property"の値を返す.
詳細とオプション




- LocationEquivalenceTestは,母集団の真の位置母数が等しい
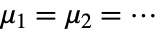 という帰無仮説
という帰無仮説 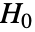 と少なくとも1つが異なるという対立仮説
と少なくとも1つが異なるという対立仮説 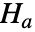 を使い,dataiについて仮説検定を行う.
を使い,dataiについて仮説検定を行う. - デフォルトで,確率の値すなわち
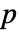 値が返される.
値が返される. - 小さい
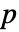 値は
値は 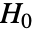 が真である可能性が低いことを示す.
が真である可能性が低いことを示す. - dataiは一変量{x1,x2,…}でなければならない.
- LocationEquivalenceTest[{data1,…}]はデータに適用できる最も強力な検定を選ぶ.
- LocationEquivalenceTest[{data1,…},All]はデータに適用できるすべての検定を選ぶ.
- LocationEquivalenceTest[{data1,…},"test"]は"test"による
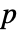 値をレポートする.
値をレポートする. - 平均値に基づく検定は dataiが正規分布に従うと仮定する.中央値に基づくクラスカル・ウォリス(Kruskal–Wallis)検定は dataiが共通の中央値について対称であると仮定する.完全ブロック
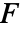 検定とフリードマン(Friedman)順位検定はデータが完全乱塊にあると仮定する.いずれの検定でも dataiの分散が同じであることが求められる.
検定とフリードマン(Friedman)順位検定はデータが完全乱塊にあると仮定する.いずれの検定でも dataiの分散が同じであることが求められる. - 使用可能な検定
-
"CompleteBlockF" 正規性,ブロック法 完全ブロック法のための平均検定 "FriedmanRank" ブロック法 完全ブロック法のための中央値検定 "KruskalWallis" 対称性 2つ以上のサンプルについての中央値検定 "KSampleT" 正規性 2つ以上のサンプルについての平均検定 - 完全ブロック
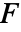 検定は,事実上,完全乱塊法の一元配置分散分析を行う.
検定は,事実上,完全乱塊法の一元配置分散分析を行う. - フリードマン順位検定はデータの行ごとに観測値を順位付けし,各列で順位の合計を求めることで検定統計量を求める.検定統計量は,同順位については修正される.
- クラスカル・ウォリス検定は,事実上データの順位について一元配置分散分析を行う.検定統計量は,同順位については修正される.
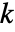 サンプルの
サンプルの 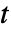 検定は,データの一元配置分散分析に等しい.
検定は,データの一元配置分散分析に等しい.- LocationEquivalenceTest[{data1,…},"HypothesisTestData"]は,htd["property"]という形で追加的な検定結果と特性を抽出するのに使えるHypothesisTestDataオブジェクト htd を返す.
- LocationEquivalenceTest[{data1,…},"property"]を使って"property"の値を直接与えることができる.
- 検定結果のレポートに関連する特性
-
"AllTests" 適用可能なすべての検定のリスト "AutomaticTest" Automaticが使われた場合に選ばれる検定 "DegreesOfFreedom" 検定で使われる自由度 "PValue" 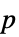 値のリスト
値のリスト"PValueTable" 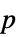 値のフォーマットされた表
値のフォーマットされた表"ShortTestConclusion" 検定結果の簡単な説明 "TestConclusion" 検定結果の説明 "TestData" 検定統計量と 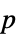 値のペアのリスト
値のペアのリスト"TestDataTable" 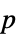 値と検定統計量のフォーマットされた表
値と検定統計量のフォーマットされた表"TestStatistic" 検定統計量のリスト "TestStatisticTable" 検定統計量のフォーマットされた表 - 使用可能なオプション
-
Method Automatic 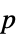 値の計算に使うメソッド
値の計算に使うメソッドSignificanceLevel 0.05 診断とレポートのための切捨て VerifyTestAssumptions Automatic 証明すべき仮定 - 位置検定では,
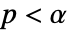 のときにのみ
のときにのみ 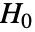 が棄却されるような切捨て
が棄却されるような切捨て 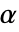 が選ばれる."TestConclusion"および"ShortTestConclusion"特性に使われる
が選ばれる."TestConclusion"および"ShortTestConclusion"特性に使われる 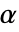 の値はSignificanceLevelオプションで制御される.値
の値はSignificanceLevelオプションで制御される.値 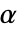 は正規性,等分散性,対称性の検定等を含む仮定の診断検定にも使われる.デフォルトで,
は正規性,等分散性,対称性の検定等を含む仮定の診断検定にも使われる.デフォルトで,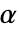 は0.05に設定されている.
は0.05に設定されている. - LocationEquivalenceTestのVerifyTestAssumptionsの名前付き設定値
-
"Normality" すべてのデータが正規分布に従うことを証明 "EqualVariance" dataiの分散が等しいことを証明 "Symmetry" 共通の平均値について対称であることを証明
例題
すべて開く すべて閉じる例 (3)
2つ以上の母集団の平均あるいは中央値がすべて等しいかどうかの検定を行う:
特性を繰り返し抽出するためにHypothesisTestDataオブジェクトを作る:
完全ブロック ![]() 検定を使って完全ブロック法の平均差の検定を行うことができる:
検定を使って完全ブロック法の平均差の検定を行うことができる:
スコープ (9)
検定 (5)
特性"AllTests"を使ってどの検定が使われたかを調べる:
繰り返して特性を抽出するためにHypothesisTestDataオブジェクトを作る:
HypothesisTestDataオブジェクトからいくつかの特性を抽出する:
オプション (8)
Method (2)
再スケールされた検定統計量はFRatioDistributionに従う:
SignificanceLevel (3)
アプリケーション (4)
最初のデータ集合群は,全く異なる位置を持つ母集団から引き出された:
2種類のカニの形態学的な寸法が2つの性のそれぞれについて取られた.さまざまな群において寸法が異なるかどうかを判断する:
性と種類を同時に考慮に入れると,すべての寸法は有意的に異なる:
特定の薬で目標の体重減量を達成できなかった2型糖尿病の患者75人に対して,試験的研究が行われた.患者は,ランダムに3つの群(もとの薬を飲み続けた対照群,およびそれぞれ50mgと100mgの新しい薬を投与された2つの治療群)に分けられた.12週間における減量をポンドで記録した:
それぞれ対の差分の検定においてBonferroni修正を使うと,どちらの治療レベル群も対照群よりよい結果であるが,お互いにはあまり違いのないことが分かる:
6人の料理評論家が4軒のレストランの品質について100点満点で評価を行った.この評価に照らして,4件のレストランの品質に有意差が見られるかどうかを考える:
特性と関係 (12)
![]() サンプルの
サンプルの ![]() 検定で返された
検定で返された ![]() 値は,2サンプルのTTestのそれに等しい:
値は,2サンプルのTTestのそれに等しい:
クラスカル・ウォリス検定は2サンプルのマン-ホイットニー(Mann–Whitney)検定の ![]() サンプル拡張である:
サンプル拡張である:
マン-ホイットニーの ![]() 値は,連続性とタイについて修正される:
値は,連続性とタイについて修正される:
![]() において
において ![]() サンプルの
サンプルの ![]() 検定の統計量は,g がデータ集合数,n が観察の合計数であるFRatioDistribution[g-1,n-g]に従う:
検定の統計量は,g がデータ集合数,n が観察の合計数であるFRatioDistribution[g-1,n-g]に従う:
![]() の下では,t 処理と g ブロックの完全ブロック
の下では,t 処理と g ブロックの完全ブロック ![]() 検定とフリードマンの順位検定統計量はFRatioDistribution[t-1,(g-1)(t-1)]に従う:
検定とフリードマンの順位検定統計量はFRatioDistribution[t-1,(g-1)(t-1)]に従う:
フリードマン統計を変換してChiSquareDistribution[g-1]に従うようにすることができる:
ChiSquareDistributionを使って ![]() 値を計算する:
値を計算する:
Methodを"Asymptotic"に設定すると自動的にこの変換が行われる:
![]() においてクラスカル・ウォリス検定の統計量は,g がデータ集合数である ChiSquareDistribution[g-1]に漸近的に従う:
においてクラスカル・ウォリス検定の統計量は,g がデータ集合数である ChiSquareDistribution[g-1]に漸近的に従う:
デフォルトで検定統計量はFRatioDistribution[g-1,n-g]に従うように再スケールされる:
LocationEquivalenceTestは事実上この割合がどのくらい1から離れているかを検出する:
![]() および
および ![]() の検定統計量がLocationEquivalenceTestで使われる:
の検定統計量がLocationEquivalenceTestで使われる:
![]() 個のサンプルの
個のサンプルの ![]() 検定とクラスカル・ウォリス検定では,LinearModelFitを使って統計量を計算することができる:
検定とクラスカル・ウォリス検定では,LinearModelFitを使って統計量を計算することができる:
2つのデータ集合についてLocationTestを使う:
LocationTestはより複雑な仮説についての検定を行うこともできる:
位置の等価性検定は,入力がTimeSeriesのときはタイムスタンプを無視する:
位置の等価性に関する検定は,TemporalDataの経路構造を認識する:
考えられる問題 (3)
テキスト
Wolfram Research (2010), LocationEquivalenceTest, Wolfram言語関数, https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html.
CMS
Wolfram Language. 2010. "LocationEquivalenceTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html.
APA
Wolfram Language. (2010). LocationEquivalenceTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html
BibTeX
@misc{reference.wolfram_2025_locationequivalencetest, author="Wolfram Research", title="{LocationEquivalenceTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html}", note=[Accessed: 14-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_locationequivalencetest, organization={Wolfram Research}, title={LocationEquivalenceTest}, year={2010}, url={https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html}, note=[Accessed: 14-February-2026]}
