LocationEquivalenceTest

LocationEquivalenceTest[{data1,data2,…}]

检验 datai 的均值或中位数是否相等.

LocationEquivalenceTest[{data1,…},"property"]

返回 "property" 的值.

更多信息和选项

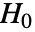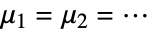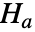  • LocationEquivalenceTest 在 datai 上进行假设检验时，零假设 假定总体的真实位置参数相等，即 ，备择假设 认为至少有一个是不同的.
  • 缺省返回一个概率值或称 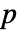值.
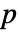  • 小的 值表明 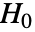不可能为真.
  • datai 必须为一元型 {x1,x2,…}.
  • LocationEquivalenceTest[{data1,…}] 将根据数据选择效能最强的检验方法.
  • LocationEquivalenceTest[{data1,…},All] 将选择适用于数据的所用检验.
  • LocationEquivalenceTest[{data1,…},"test"] 报告基于 "test" 的 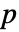值.
  • 基于均值的检验假定 datai 服从正态分布. 基于中位数的 Kruskal–Wallis 检验假定 datai 关于一个公共中位数对称. 完整区组 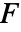和 Friedman 秩检验都假定数据位于随机的完整区组中. 两种检验类型都要求 datai 有相等的方差.
  • 可以使用下列检验：
  • "CompleteBlockF"正态性，区组化完全区组设计的均值检验
    "FriedmanRank"区组化完全区组设计的中位数检验
    "KruskalWallis"对称性两个或者更多个样本的中位数检验
    "KSampleT"正态性两个或者更多个样本的均值检验
  • 完全区组 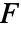检验实际上对随机完全区组设计执行单向方差分析.
  • Friedman 秩检验在各行上对观测结果进行排序，并且对数据上各列的秩求和，以得到检验统计量. 在出现等值的情况下，对统计量进行校正.
  • Kruskal–Wallis 检验对数据的秩执行单向方差分析.在出现等值的情况下，对统计量进行校正.
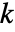  • 样本 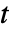检验等价于数据的单向方差分析.
  • LocationEquivalenceTest[{data1,…},"HypothesisTestData"] 返回一个 HypothesisTestData 对象 htd，该对象可以通过利用格式 htd["property"] 提取额外的检验结果和属性.
  • LocationEquivalenceTest[{data1,…},"property"] 可用于直接给出 "property" 的值.
  • 与检验结果报告相关的性质包括：
  • "AllTests"所有适用检验的列表
    "AutomaticTest"使用 Automatic 时所选择的检验
    "DegreesOfFreedom"检验中所用的自由度
    "PValue" 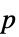值列表
    "PValueTable" 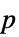值的格式化表格
    "ShortTestConclusion"检验结论的简单说明
    "TestConclusion"检验结论的说明
    "TestData"检验统计量与 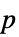值的数对列表
    "TestDataTable" 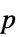值与检验统计量的格式化表格
    "TestStatistic"检验统计量的列表
    "TestStatisticTable"检验统计量的格式化表格
  • 可以给出下列选项：
  • Method Automatic用于计算 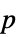值的方法
    SignificanceLevel 0.05诊断与报告的截止值
    VerifyTestAssumptions Automatic应该验证的假定
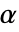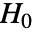  • 对于位置检验，所选择的截止值 使得 仅在 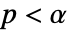时被拒绝. 用于 "TestConclusion" 和 "ShortTestConclusion" 属性的 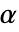值由 SignificanceLevel 选项控制. 值 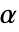同时用于包括正态性、等方差与对称性检验在内的假定的诊断检验. 默认情况下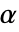， 设为 0.05.
  • 在 LocationEquivalenceTest 中，VerifyTestAssumptions 的命名设置包括：
  • "Normality"验证所有数据为正态分布
    "EqualVariance"验证 datai 的方差相等
    "Symmetry"验证关于一个共同的中位数的对称性

范例

打开所有单元关闭所有单元

基本范例  (3)

检验两个总体或更多总体的均值或中位数是否相等：

对于重复提取的性质，创建一个 HypothesisTestData 对象：

完全区组 检验可用于检验完全区组设计的均值差：

在 0.05 显著性水平下，均值之间有显著的差异：

利用 Friedman 秩检验来检测完全区组设计下的中位数差：

可以看出，至少有一个中位数与其它有显著的不同：

范围  (9)

检验  (5)

进行一个特定的等位置检验：

可以同时进行任意个数的检验：

同时进行适用于数据的所有检验：

使用性质 "AllTests" 识别所用的检验方法：

对于重复提取的性质，创建一个 HypothesisTestData 对象：

可以提取的性质：

从一个 HypothesisTestData 对象中提取某些性质：

一个 样本 检验的 值与检验统计量：

同时提取任意个性质：

一个 Kruskal-Wallis 检验的 值与检验统计量：

报告  (4)

将所选择的一组检验结果制成表格形式：

全部适用检验结果的完整表格：

所选择的检验结果的表格：

恢复检验表格中的各项，生成自定义的报告：

值高于 0.05，因此在该水平拒绝 的证据不足：

制作一个检验或一组检验的 值表：

表中的 值：

全部适用检验的 值表：

一部分检验的 值表：

报告一个或一组检验的检验统计量：

表格中的检验统计量：

所有适当检验的检验统计量表格：

选项  (8)

Method  (2)

对一组数据集，计算 Kruskal–Wallis 检验：

经过尺度缩放后的检验统计量服从 FRatioDistribution：

使用渐进的卡方近似：

对 Friedman 秩检验，利用渐进卡方分布：

默认情况下，使用Conover 的 分布近似：

SignificanceLevel  (3)

设置诊断检验的显著性水平：

默认水平是 0.05：

设置显著性水平可能改变自动选择的检验方法：

默认情况下，选择基于中位数的检验方法：

对 "TestConclusion" 和 "ShortTestConclusion" 也使用显著性水平：

VerifyTestAssumptions  (3)

利用 All 或者 None，可以将诊断按分组方式控制：

验证所有假定：

不对假定进行检查：

可以独立控制诊断：

假定正态性，对对称性进行检查：

只检查正态性：

可以显式设置检验假定值：

因为数据不服从正态分布，前面选择了 Kruskal-Wallis 检验：

应用  (4)

检验一组总体是否共享一个共同的位置：

第一组数据集从总体中位置差别很大的地方抽取：

由第二组表示的总体都有相似的位置：

这里有两种不同的螃蟹，分别对雌雄两种螃蟹测量一些形态学特征. 判断在不同组中这些测量结果是否不同：

当忽略类别时，尾部宽度是体现性别差异的唯一测量结果：

当我们同时考虑性别和种类时，所有的测量结果都有显著的不同：

对 75 个患有II型糖尿病的病人进行一项前导性研究，这些病人在某种特定药物治疗下没有达到预期的减肥目标. 把这些病人随机分成3组：一个对照组继续之前的药物治疗，两个治疗组接受剂量分别为50和100毫克的新药物的治疗. 记录 12 周内的体重减少量（以磅为单位）：

在各组的均值之间有显著不同：

在成对差值检验中，使用 Bonferroni 校正，结果显示这两个治疗组的水平高于对照组，但是它们彼此之间没有显著不同：

6 位食品评论家对四个餐馆的质量进行评估，他们采用的是 100 分制的评估方法. 根据这些评估结果，判断这四家餐馆的质量是否有显著差异：

由评论家给分的中位数组成的条形图：

由每个餐馆得到的分数的中位数组成的条形图：

使用区组结构，我们可以检测到质量上有显著差异：

属性和关系  (12)

由 样本 检验返回的 值等价于两个样本的 TTest 得到的值：

Kruskal–Wallis检验是双样本Mann–Whitney检验的一个 样本扩展：

对连续性和均值进行 Mann–Whitney 值校正：

在 下， 样本 检验的统计量服从一个 FRatioDistribution[g-1,n-g]，其中 g 是数据集的数目，而 n 是测量结果的总数：

在 下，完全区组 和 Friedman 秩检验统计量（带有 t 个处理方法和 g 个区组）服从一个 FRatioDistribution[t-1,(g-1)(t-1)]：

可以对 Friedman 统计量进行变换，使之服从 ChiSquareDistribution[g-1]：

利用 ChiSquareDistribution 计算 值：

通过把 Method 设为 "Asymptotic"，自动完成变换：

在 下，Kruskal–Wallis检验统计量渐进服从ChiSquareDistribution[g-1]，其中 g 是数据集的数目：

默认情况下，对检验统计量重新调整尺寸以服从 FRatioDistribution[g-1,n-g]：

从概念上，比较合并方差与平均单个方差：

较大的合并方差表示不同的均值：

合并方差与单个方差的比值：

LocationEquivalenceTest 检验这个比值与1的差异有多大：

和 检验统计量也用于 LocationEquivalenceTest 中：

Kruskal–Wallis统计量是基于排序的：

对于 样本 和 Kruskal–Wallis检验，检验统计量可以使用 LinearModelFit 计算得到：

一个设计矩阵：

样本 检验：

Kruskal–Wallis检验是类似的，但它使用了排序方法：

对两组数据使用 LocationTest：

结果是相等的：

LocationTest 也可以检验更复杂的假设：

输入是 TimeSeries 时位置等价测试会忽略时间戳：

位置等效检验可以识别 TemporalData 的路径结构：

直接对数值进行计算：

可能存在的问题  (3)

所有的检验要求数据有相等的方差：

样本 检验和完全区组 检验要求数据服从正态分布：

如果数据不服从正态分布，那么应该使用 Kruskal–Wallis 检验或者 Friedman秩检验：

Friedman 秩和完全区组 检验要求相等的样本大小：

巧妙范例  (1)

当零假设 为真时，计算统计量：

给定特定的备择假设，检验统计量：

比较检验统计量的分布：

Wolfram Research (2010)，LocationEquivalenceTest，Wolfram 语言函数，https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html.

文本

Wolfram Research (2010)，LocationEquivalenceTest，Wolfram 语言函数，https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html.

CMS

Wolfram 语言. 2010. "LocationEquivalenceTest." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html.

APA

Wolfram 语言. (2010). LocationEquivalenceTest. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html 年

BibTeX

@misc{reference.wolfram_2024_locationequivalencetest, author="Wolfram Research", title="{LocationEquivalenceTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_locationequivalencetest, organization={Wolfram Research}, title={LocationEquivalenceTest}, year={2010}, url={https://reference.wolfram.com/language/ref/LocationEquivalenceTest.html}, note=[Accessed: 21-November-2024 ]}