Log
Log[z]
gives the natural logarithm of z (logarithm to base ![]() ).
).
Log[b,z]
gives the logarithm to base b.
Details

- Log is a mathematical function, suitable for both symbolic and numerical manipulation.
- Log gives exact rational number results when possible.
- For certain special arguments, Log automatically evaluates to exact values.
- Log can be evaluated to arbitrary numerical precision.
- Log automatically threads over lists.
- Log[z] has a branch cut discontinuity in the complex z plane running from
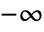 to
to 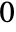 .
. - Log can be used with Interval and CenteredInterval objects. »
Examples
open allclose allBasic Examples (6)
Scope (51)
Numerical Evaluation (7)
Evaluate numerically to high precision:
The precision of the output tracks the precision of the input:
Evaluate Log efficiently at high precision:
Log threads elementwise over lists and matrices:
It threads over lists in either argument:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix Log function using MatrixFunction:
Specific Values (5)
Visualization (3)
Function Properties (12)
Log[z] gives the logarithm with base E:
Log is defined for all real positive values:
Log achieves all real values:
The issue is a branch cut along the negative real axis:
The branch cut exists for any fixed value of ![]() :
:
![]() is increasing on the positive reals for
is increasing on the positive reals for ![]() and decreasing for
and decreasing for ![]() :
:
Log is injective:
Log is surjective:
Log is neither non-negative nor non-positive:
![]() has both singularities and discontinuities for x≤0:
has both singularities and discontinuities for x≤0:
![]() is concave on the positive reals for
is concave on the positive reals for ![]() and convex for
and convex for ![]() :
:
TraditionalForm formatting:
Differentiation (5)
Series Expansions (5)
Function Identities and Simplifications (6)
Basic identity for Log:
Logarithm of a power function simplification:
Function Representations (5)
Log arises from the power function in a limit:
Log can be represented in terms of MeijerG:
Log can be represented as a DifferentialRoot:
Generalizations & Extensions (2)
Applications (8)
Plot Log for various bases:
Plot the real and imaginary parts of Log:
Plot the real and imaginary parts over the complex plane:
Plot data logarithmically and doubly logarithmically:
Benford's law predicts that the probability of the first digit is ![]() in many sequences:
in many sequences:
Analyze the first digits of the following sequence:
Use Tally to count occurrences of each digit:
Shannon entropy for a set of probabilities:
Equi‐entropy surfaces for four symbols:
Approximate the ![]()
![]() prime number:
prime number:
Exponential divergence of two nearby trajectories for a quadratic map:
Properties & Relations (13)
Compositions with the inverse function might need PowerExpand:
Get expansion that is correct for all complex arguments:
Simplify logarithms with assumptions:
Convert inverse trigonometric and hyperbolic functions into logarithms:
Log arises from the power function in a limit:
Solve a logarithmic equation:
Reduce a logarithmic equation:
Numerically find a root of a transcendental equation:
The natural logarithms of integers are transcendental:
Integral transforms:
Solve differential equations:
Limits:
Log is automatically returned as a special case for various special functions:
Possible Issues (7)
For a symbolic base, the base b log evaluates to a quotient of logarithms:
Generically, ![]() :
:
Because intermediate results can be complex, approximate zeros can appear:
Machine-precision inputs can give numerically wrong answers on branch cuts:
Use arbitrary‐precision arithmetic to obtain correct results:
Compositions of logarithms can give functions that are zero almost everywhere:
This function is a differential-algebraic constant:
Logarithmic branch cuts can occur without their corresponding branch point:
The argument of the logarithm never vanishes:
But it can take negative values, so the logarithm has a branch cut:
The kink at ![]() marks the appearance of the second sheet:
marks the appearance of the second sheet:
Logarithmic terms in Puiseux series are considered coefficients inside SeriesData:
In traditional form, parentheses are needed around the argument:
Text
Wolfram Research (1988), Log, Wolfram Language function, https://reference.wolfram.com/language/ref/Log.html (updated 2021).
CMS
Wolfram Language. 1988. "Log." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Log.html.
APA
Wolfram Language. (1988). Log. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Log.html