MannWhitneyTest
MannWhitneyTest[{data1,data2}]
检验 data1 和 data2 的中位数是否相等.
MannWhitneyTest[dspec,μ0]
对 μ0 检验中位数差值.
MannWhitneyTest[dspec,μ0,"property"]
返回 "property" 的值.
更多信息和选项



- MannWhitneyTest 在 data1 和 data2 上执行一个假设检验,其中零假设
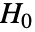 为真正的中位数差值
为真正的中位数差值 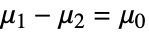 ⟷
⟷ 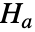 即
即 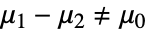 .
. - 默认情况下,返回一个概率值或者
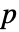 值.
值. - 一个较小的
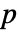 值表明
值表明 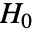 不可能为真.
不可能为真. - dspec 中的数据可以是单变量 {x1,x2,…} 或者多变量 {{x1,y1,…},{x2,y2,…},…}.
- 变量 μ0 可以是一个实数,或者是长度等于数据维度的实向量.
- MannWhitneyTest 假设在多变量情况下,数据关于共同的空间中位数呈椭圆形地对称.
- MannWhitneyTest[dspec,μ0,"HypothesisTestData"] 返回一个 HypothesisTestData 对象 htd,可以使用 htd["property"] 的形式来提取额外检验结果和属性.
- MannWhitneyTest[dspec,μ0,"property"] 可以用于直接给出 "property" 值.
- 与检验结果报告相关的属性包括:
-
"DegreesOfFreedom" 检验中所使用的自由度 "PValue" 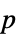 值列表
值列表"PValueTable" 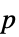 值组成的格式化表格
值组成的格式化表格"ShortTestConclusion" 检验结论的简短描述 "TestConclusion" 检验结论的描述 "TestData" 检验统计量和 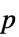 值对的列表
值对的列表"TestDataTable" 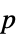 值和检验统计量组成的格式化表格
值和检验统计量组成的格式化表格"TestStatistic" 检验统计量组成的列表 "TestStatisticTable" 检验统计量组成的格式化表格 - 可以使用以下选项:
-
AlternativeHypothesis "Unequal" 备择假设的不等性 MaxIterations Automatic 多变量中位数检验的最大迭代 Method Automatic 用于 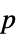 值的方法
值的方法SignificanceLevel 0.05 用于诊断和报告的分界点 - 对于单变量样本,MannWhitneyTest 对独立样本的中位数差异进行 Mann–Whitney
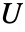 检验. 可使用以下方法:
检验. 可使用以下方法: -
Automatic 根据样本量选择 "Asymptotic" 大样本统计量是渐近正态分布的 "Exact" 小样本的 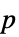 值可以精确计算
值可以精确计算"Permutation" 基于模拟 - 对于“渐近法”和“置换法”,会对并列关系进行校正;对检验统计量进行连续性校正,并假定其服从 NormalDistribution.
- 对于多元样本,MannWhitneyTest 使用空间等级对 Mann–Whitney
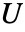 检验进行扩展. 假设检验统计量渐近遵循 ChiSquareDistribution[dim],其中 dim 是 dspec 的维数.
检验进行扩展. 假设检验统计量渐近遵循 ChiSquareDistribution[dim],其中 dim 是 dspec 的维数. - 对于 MannWhitneyTest,选择一个临界值
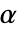 ,使得当且仅当
,使得当且仅当 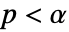 时,否定
时,否定 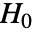 . 用于 "TestConclusion" 和 "ShortTestConclusion" 属性的
. 用于 "TestConclusion" 和 "ShortTestConclusion" 属性的 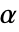 值由 SignificanceLevel 选项控制. 默认情况下,
值由 SignificanceLevel 选项控制. 默认情况下,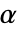 设为 0.05.
设为 0.05.
范例
打开所有单元关闭所有单元基本范例 (2)
范围 (9)
检验 (6)
创建一个 HypothesisTestData 对象,用于进行重复属性提取:
从 HypothesisTestData 对象提取某些属性:
推广和延伸 (2)
选项 (12)
AlternativeHypothesis (4)
Method (5)
应用 (3)
属性和关系 (4)
对于单变量数据,在 ![]() 下,检验统计量服从 NormalDistribution[0,1]:
下,检验统计量服从 NormalDistribution[0,1]:
对 NormalDistribution 的大样本近似:
对于多变量数据,在 ![]() 下,检验统计量服从 ChiSquareDistribution[p]:
下,检验统计量服从 ChiSquareDistribution[p]:
在没有相等数据出现的情况下,Ordering 可以用来计算排序:
精确的 ![]() 值与在给定数据集大小的情况下考虑每种可能的置换时的检验统计量频率相匹配:
值与在给定数据集大小的情况下考虑每种可能的置换时的检验统计量频率相匹配:
文本
Wolfram Research (2010),MannWhitneyTest,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MannWhitneyTest.html.
CMS
Wolfram 语言. 2010. "MannWhitneyTest." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MannWhitneyTest.html.
APA
Wolfram 语言. (2010). MannWhitneyTest. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MannWhitneyTest.html 年