WOLFRAM

Wolfram Language & System Documentation Center

MardiaSkewnessTest[data]

tests whether data follows a MultinormalDistribution using the Mardia skewness test.

MardiaSkewnessTest[data,"property"]

returns the value of "property".

Details and Options
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Testing  
Reporting  
Options  
Method  
SignificanceLevel  
Applications  
Properties & Relations  
Possible Issues  
Neat Examples  
See Also
Related Guides
History
Cite this Page

MardiaSkewnessTest

MardiaSkewnessTest[data]

tests whether data follows a MultinormalDistribution using the Mardia skewness test.

MardiaSkewnessTest[data,"property"]

returns the value of "property".

Details and Options

  • MardiaSkewnessTest performs the Mardia skewness goodness-of-fit test with null hypothesis 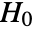that data was drawn from a MultinormalDistribution and alternative hypothesis 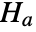that it was not.
  • By default, a probability value or 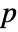-value is returned.
  • A small 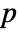-value suggests that it is unlikely that the data is normally distributed.
  • The data can be univariate {x1,x2,…} or multivariate {{x1,y1,…},{x2,y2,…},…}.
  • The Mardia skewness test effectively compares a multivariate measure of skewness for data to a MultinormalDistribution.
  • MardiaSkewnessTest[data,dist,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
  • MardiaSkewnessTest[data,dist,"property"] can be used to directly give the value of "property".
  • Properties related to the reporting of test results include:
  • "DegreesOfFreedom"the degrees of freedom used in a test
    "PValue"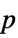-value
    "PValueTable"formatted version of "PValue"
    "ShortTestConclusion"a short description of the conclusion of a test
    "TestConclusion"a description of the conclusion of a test
    "TestData"test statistic and 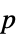-value
    "TestDataTable"formatted version of "TestData"
    "TestStatistic"test statistic
    "TestStatisticTable"formatted "TestStatistic"
  • The following properties are independent of which test is being performed.
  • Properties related to the data distribution include:
  • "FittedDistribution"fitted distribution of data
    "FittedDistributionParameters"distribution parameters of data
  • The following options can be given:
  • Method Automaticthe method to use for computing 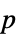-values
    SignificanceLevel 0.05cutoff for diagnostics and reporting
  • For a test for goodness-of-fit, a cutoff 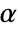is chosen such that 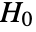is rejected only if 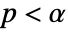. The value of 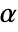used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. By default, 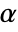is set to 0.05.
  • The following methods can be used to compute 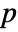-values:
  • Automaticcorrect for small samples up to dimension 5
    "Asymptotic"use the asymptotic distribution of the test statistic
    "MonteCarlo"use Monte Carlo simulation
  • With the setting Method-> "MonteCarlo", 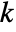datasets of the same length as the input 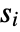are generated under 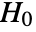using the fitted distribution. The EmpiricalDistribution from MardiaSkewnessTest[si,"TestStatistic"] is then used to estimate the 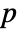-value.

Examples

open all close all

Basic Examples  (3)

Perform a test for multivariate normality:

Extract the test statistic from the Mardia skewness test:

Obtain a formatted test table:

Scope  (6)

Testing  (3)

Perform a Mardia skewness test for multivariate normality:

The -value for the normal data is large compared to the -value for the non-normal data:

Test some data for univariate normality:

Create a HypothesisTestData object for repeated property extraction:

The properties available for extraction:

Reporting  (3)

Tabulate the results of the Mardia skewness test:

The full test table:

A -value table:

The test statistic:

Retrieve the entries from a Mardia skewness test table for custom reporting:

Report test conclusions using "ShortTestConclusion" and "TestConclusion":

The conclusion may differ at a different significance level:

Options  (4)

Method  (3)

Use Monte Carlo-based methods or a computation formula:

Set the number of samples to use for Monte Carlo-based methods:

The Monte Carlo estimate converges to the true -value with increasing samples:

Set the random seed used in Monte Carlo-based methods:

The seed affects the state of the generator and has some effect on the resulting -value:

SignificanceLevel  (1)

Set the significance level used for "TestConclusion" and "ShortTestConclusion":

By default, 0.05 is used:

Applications  (2)

A power curve for the Mardia skewness test:

Visualize the approximate power curve:

Estimate the power of the Mardia skewness test when the underlying distribution is a MultivariateTDistribution, the test size is 0.05, and the sample size is 12:

Measures of petal and sepal dimensions for three varieties of iris were recorded. A multivariate test of means can be used as a quick check that the measures might be useful in discriminating between two similar species but is only valid if the data follows a multivariate normal distribution:

The multivariate skewness of the two species is similar to a multivariate normal distribution:

The multivariate kurtosis should also be checked to confirm normality:

The data appears normal, so TTest is valid:

Properties & Relations  (4)

The multivariate test statistic:

Under the test statistic follows a ChiSquareDistribution:

The univariate test statistic:

Under the test statistic follows a ChiSquareDistribution[1]:

Mardia's skewness test can only detect departures from normality in skewness:

The data is clearly not normally distributed:

Decisions should be based on MardiaSkewnessTest and MardiaKurtosisTest:

The Mardia skewness test works with the values only when the input is a TimeSeries:

Possible Issues  (1)

If the covariance matrix of the data is not positive definite, the test will fail:

The number of data points must be greater than the dimension of the data:

Neat Examples  (1)

Compute the statistic when the null hypothesis is true:

The test statistic given a particular alternative:

Compare the distributions of the test statistics:

Wolfram Research (2010), MardiaSkewnessTest, Wolfram Language function, https://reference.wolfram.com/language/ref/MardiaSkewnessTest.html.

Text

Wolfram Research (2010), MardiaSkewnessTest, Wolfram Language function, https://reference.wolfram.com/language/ref/MardiaSkewnessTest.html.

CMS

Wolfram Language. 2010. "MardiaSkewnessTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MardiaSkewnessTest.html.

APA

Wolfram Language. (2010). MardiaSkewnessTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MardiaSkewnessTest.html

BibTeX

@misc{reference.wolfram_2025_mardiaskewnesstest, author="Wolfram Research", title="{MardiaSkewnessTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/MardiaSkewnessTest.html}", note=[Accessed: 31-October-2025]}

BibLaTeX

@online{reference.wolfram_2025_mardiaskewnesstest, organization={Wolfram Research}, title={MardiaSkewnessTest}, year={2010}, url={https://reference.wolfram.com/language/ref/MardiaSkewnessTest.html}, note=[Accessed: 31-October-2025]}