MaxValue
✖
MaxValue
更多信息和选项



- MaxValue 亦称为上确界.
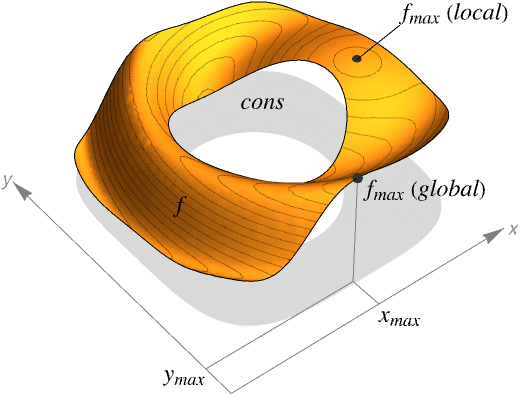
- MaxValue 求在给定约束条件限制下 f 的全局最大值.
- MaxValue 通常用于求给定约束条件下可能的最大值. 在不同的领域,这可能被称为最佳策略、最佳方案、最佳配置等.
- Maximize 返回形为 {fmax,{x->xmax,y->ymax,…}} 的列表.
- 如果 f 和 cons 是线性的或是多项式,MaxValue 总是求全局上确界.
- 约束条件 cons 可以是以下表达式的任意逻辑组合:
-
lhs==rhs 等式 lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs 不等式 (LessEqual、…) lhsrhs, lhsrhs, lhsrhs, lhsrhs 向量不等式 (VectorLessEqual、…) Exists[…], ForAll[…] 量化的条件 {x,y,…}∈rdom 区域或域的指定 - MaxValue[{f,cons},x∈rdom] 实际上等价于 MaxValue[{f,cons∧x∈rdom},x].
- 对于 x∈rdom,可用 Indexed[x,i] 来指代不同的坐标.
- 可能的域 rdom 包括:
-
Reals 实标量变量 Integers 整数标量变量 Vectors[n,dom] 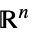 中的向量变量
中的向量变量Matrices[{m,n},dom] 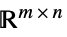 中的矩阵变量
中的矩阵变量ℛ 限制在几何区域 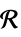 中的向量变量
中的向量变量 - 默认情况下,假定所有变量都是实数.
- 如果给定精确的输入,MaxValue 将返回精确的结果. 如果给定近似的输入,它会自动调用 NMaxValue.
- MaxValue 将返回以下形式的结果:
-
fmax 有限的最大值 -∞ 不可行,即约束集为空 ∞ 无界,即 f 的值可以是任意大的值 - MaxValue 给出 f 的值的上确界. 可能没有 x、y、… 值能实现该下确界.
- N[MaxValue[…]] 调用 NMaxValue 来解决不能以符号形式求解的优化问题.
范例
打开所有单元关闭所有单元基本范例 (5)常见实例总结
https://wolfram.com/xid/0e7mopp2-faqf4h
https://wolfram.com/xid/0e7mopp2-b6nuhh
https://wolfram.com/xid/0e7mopp2-fcm1i7
https://wolfram.com/xid/0e7mopp2-65b19
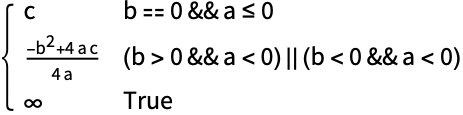
https://wolfram.com/xid/0e7mopp2-ewyjra
https://wolfram.com/xid/0e7mopp2-vvj0qt
范围 (36)标准用法实例范围调查
基本用法 (7)
https://wolfram.com/xid/0e7mopp2-trrpys
https://wolfram.com/xid/0e7mopp2-bufhg8
https://wolfram.com/xid/0e7mopp2-bm5ra5
https://wolfram.com/xid/0e7mopp2-g6h8nq
https://wolfram.com/xid/0e7mopp2-hkmi26
https://wolfram.com/xid/0e7mopp2-34w61f
https://wolfram.com/xid/0e7mopp2-4pgkbq
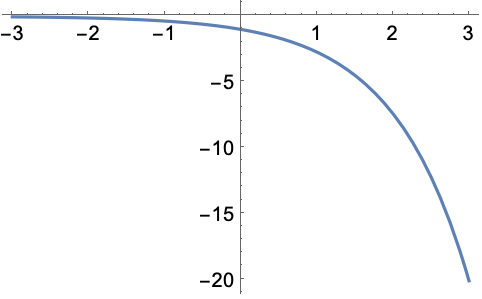
https://wolfram.com/xid/0e7mopp2-egt7s8
单变量问题 (7)
https://wolfram.com/xid/0e7mopp2-zbfxzt
https://wolfram.com/xid/0e7mopp2-68ta4k
https://wolfram.com/xid/0e7mopp2-l8bgix
https://wolfram.com/xid/0e7mopp2-5d5pbi
https://wolfram.com/xid/0e7mopp2-ff2avq
https://wolfram.com/xid/0e7mopp2-o0nmhc

https://wolfram.com/xid/0e7mopp2-8qbc8s
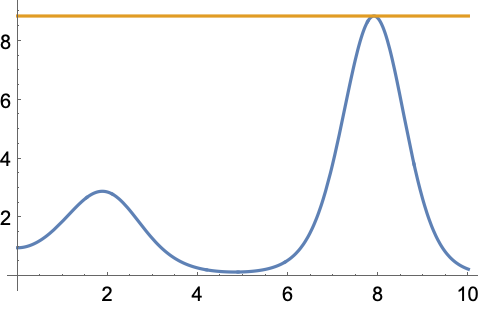
https://wolfram.com/xid/0e7mopp2-h462sn
https://wolfram.com/xid/0e7mopp2-u1hax
https://wolfram.com/xid/0e7mopp2-dsq8li
https://wolfram.com/xid/0e7mopp2-ltm55e
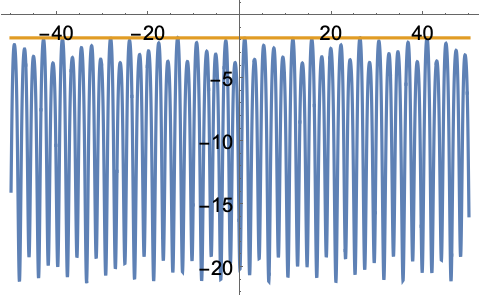
https://wolfram.com/xid/0e7mopp2-j09lw1
https://wolfram.com/xid/0e7mopp2-qqsow6
https://wolfram.com/xid/0e7mopp2-4fn5s7
多变量问题 (9)
https://wolfram.com/xid/0e7mopp2-fmnyd0
https://wolfram.com/xid/0e7mopp2-xlf7nk
https://wolfram.com/xid/0e7mopp2-ujcaiy
https://wolfram.com/xid/0e7mopp2-tn9ckb
https://wolfram.com/xid/0e7mopp2-n9l3uf
https://wolfram.com/xid/0e7mopp2-ryg9h
https://wolfram.com/xid/0e7mopp2-5c8o69
https://wolfram.com/xid/0e7mopp2-rfvdxc
https://wolfram.com/xid/0e7mopp2-9hgarl
https://wolfram.com/xid/0e7mopp2-driyp1
https://wolfram.com/xid/0e7mopp2-xds27g
https://wolfram.com/xid/0e7mopp2-6q86ky
https://wolfram.com/xid/0e7mopp2-zde7z0
https://wolfram.com/xid/0e7mopp2-3uwdvz
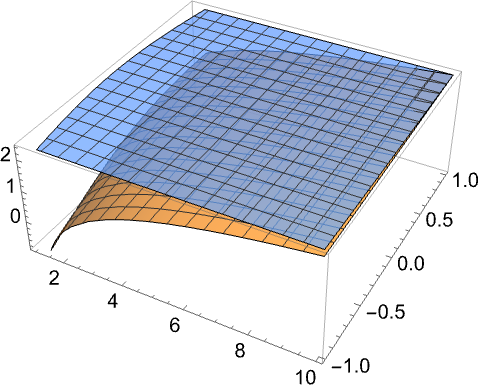
参数化问题 (4)
https://wolfram.com/xid/0e7mopp2-fdpyk1

https://wolfram.com/xid/0e7mopp2-76f0x4
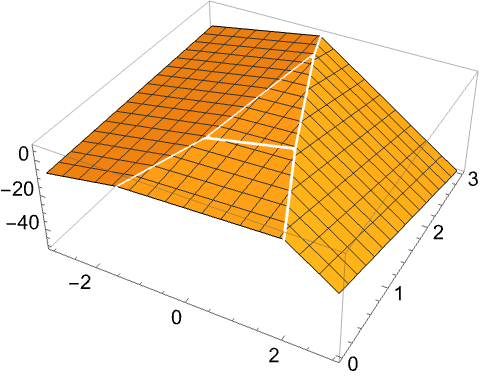
https://wolfram.com/xid/0e7mopp2-czc9ve

https://wolfram.com/xid/0e7mopp2-c3g7ko
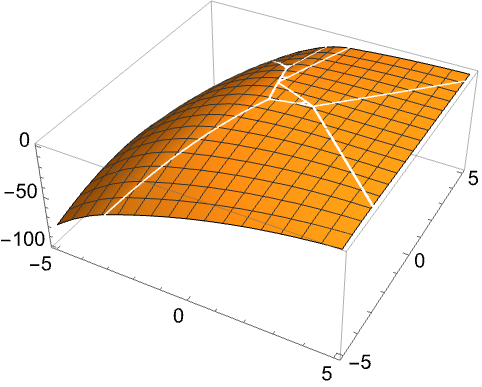
https://wolfram.com/xid/0e7mopp2-40ptyn
https://wolfram.com/xid/0e7mopp2-lskw2o
在整数上优化 (3)
https://wolfram.com/xid/0e7mopp2-n5h3ts
https://wolfram.com/xid/0e7mopp2-cafkml
https://wolfram.com/xid/0e7mopp2-ikg3fn
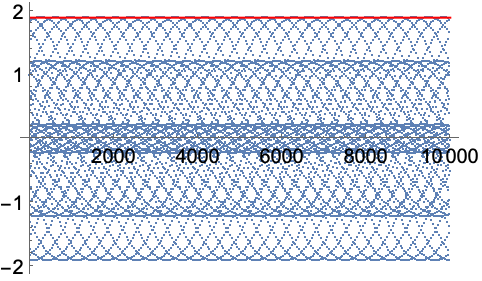
https://wolfram.com/xid/0e7mopp2-6dl90o
https://wolfram.com/xid/0e7mopp2-fnxwz0
在区域上优化 (6)
https://wolfram.com/xid/0e7mopp2-midx6o
https://wolfram.com/xid/0e7mopp2-jsii95
https://wolfram.com/xid/0e7mopp2-t9ba0s
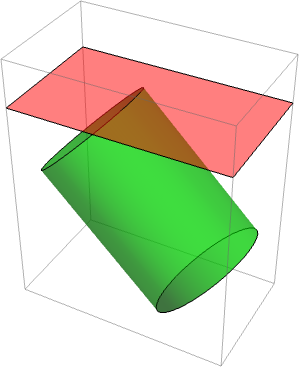
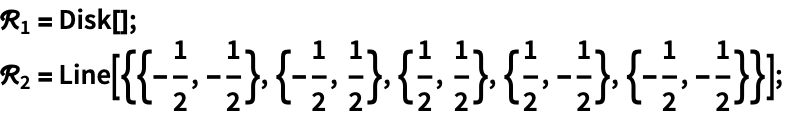
https://wolfram.com/xid/0e7mopp2-h167li
https://wolfram.com/xid/0e7mopp2-t55drh
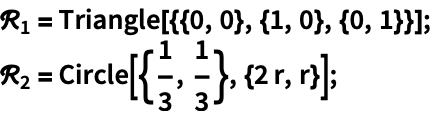
https://wolfram.com/xid/0e7mopp2-3d5r2g
https://wolfram.com/xid/0e7mopp2-wfvlvu
https://wolfram.com/xid/0e7mopp2-68q722

https://wolfram.com/xid/0e7mopp2-1uy0bz
https://wolfram.com/xid/0e7mopp2-fzcxiu
https://wolfram.com/xid/0e7mopp2-1fr9xw
https://wolfram.com/xid/0e7mopp2-st7dxt
https://wolfram.com/xid/0e7mopp2-fqzatu
https://wolfram.com/xid/0e7mopp2-v0r0w7
选项 (1)各选项的常用值和功能
WorkingPrecision (1)
https://wolfram.com/xid/0e7mopp2-dt4zl
设置 WorkingPrecision->200,我们得到一个精确的最大值,但它可能不正确:
https://wolfram.com/xid/0e7mopp2-edigmp
应用 (13)用该函数可以解决的问题范例
基本应用 (4)
https://wolfram.com/xid/0e7mopp2-wtuty
https://wolfram.com/xid/0e7mopp2-jayfl1
https://wolfram.com/xid/0e7mopp2-bx6cxm
https://wolfram.com/xid/0e7mopp2-il8afv
https://wolfram.com/xid/0e7mopp2-eg3gf2
https://wolfram.com/xid/0e7mopp2-lh3p6h
https://wolfram.com/xid/0e7mopp2-buvkpa
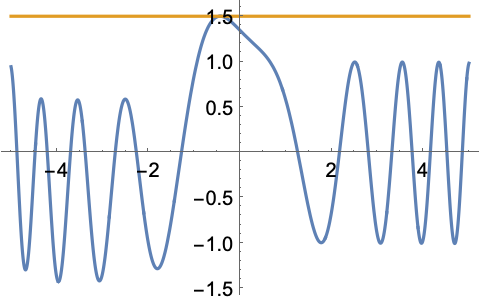
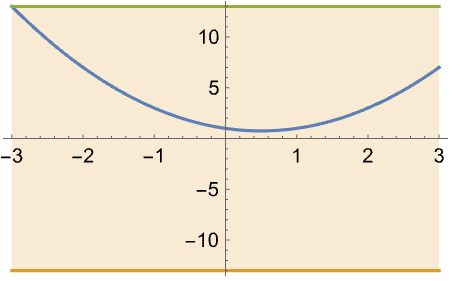
函数 f[x] 的无穷范数由 MaxValue[{Norm[f[x]],x∈},x] 给出,其中 是 f[x] 的兴趣域. 求 ![]() 在区间 {-3,3} 上的无穷范数:
在区间 {-3,3} 上的无穷范数:
https://wolfram.com/xid/0e7mopp2-dttzbo
https://wolfram.com/xid/0e7mopp2-cfooyp
https://wolfram.com/xid/0e7mopp2-4lp68
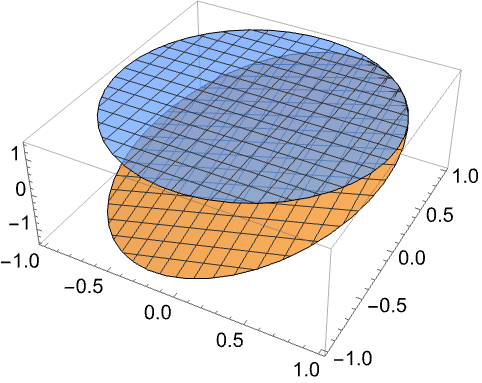
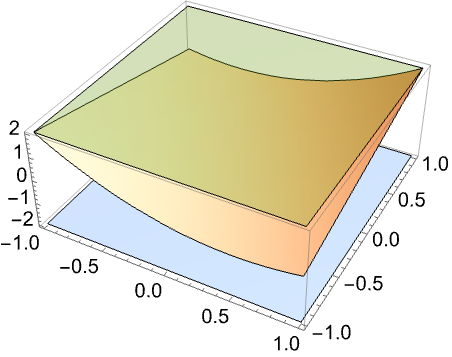
求 ![]() 在 Rectangle[{-1,-1},{1,1}] 上的无穷范数:
在 Rectangle[{-1,-1},{1,1}] 上的无穷范数:
https://wolfram.com/xid/0e7mopp2-dyeedv
https://wolfram.com/xid/0e7mopp2-cq9zj9
https://wolfram.com/xid/0e7mopp2-ibq986
几何距离 (9)
区域 ℛ 中的点到某个给定点 p 的最大距离由 MaxValue[EuclideanDistance[p,q],q∈ℛ] 给出. 求单位 Disk[] 中的点距 {1,1} 的最大距离:
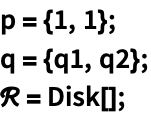
https://wolfram.com/xid/0e7mopp2-bbe5gq
https://wolfram.com/xid/0e7mopp2-ci22xk
https://wolfram.com/xid/0e7mopp2-iazhxu
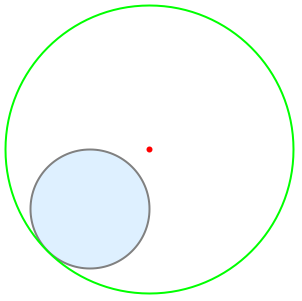
求标准单位单纯形 Simplex[2] 中的点距点 {1,3/4} 的最大距离:
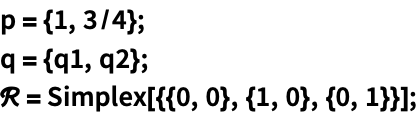
https://wolfram.com/xid/0e7mopp2-bi7hqn
https://wolfram.com/xid/0e7mopp2-bfqxai
https://wolfram.com/xid/0e7mopp2-jr1qun
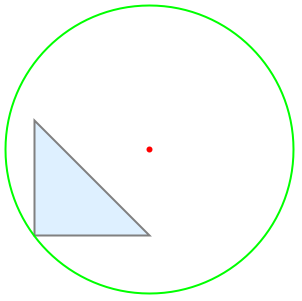
求标准单位球面 Sphere[] 上的点距点 {1,1,1} 的最大距离:

https://wolfram.com/xid/0e7mopp2-dj6j8q
https://wolfram.com/xid/0e7mopp2-dmukk8
https://wolfram.com/xid/0e7mopp2-od5y3i

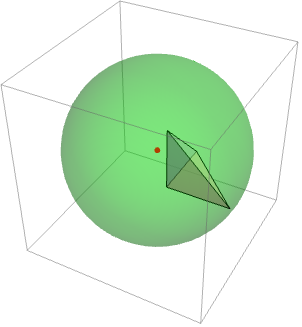
求标准单位单纯形 Simplex[3] 中的点距点 {-1/3,1/3,1/3} 的最大距离:

https://wolfram.com/xid/0e7mopp2-jqaty
https://wolfram.com/xid/0e7mopp2-k97ofe
https://wolfram.com/xid/0e7mopp2-bch17q
区域 ℛ 的直径是 ℛ 中两点间的最大距离. 可以用 MaxValue[EuclideanDistance[p,q],{p∈ℛ,q∈ℛ}] 来计算区域的直径. 求 Circle[] 的直径:
https://wolfram.com/xid/0e7mopp2-bffuv
https://wolfram.com/xid/0e7mopp2-ea32nm
求标准单位单纯形 Simplex[2] 的直径:
https://wolfram.com/xid/0e7mopp2-cj5g0j
https://wolfram.com/xid/0e7mopp2-jo71h0
求标准单位立方体 Cuboid[] 的直径:
https://wolfram.com/xid/0e7mopp2-hd6rj1
https://wolfram.com/xid/0e7mopp2-mdzx3x
可以用 MaxValue[EuclideanDistance[p,q],{p∈,q∈}] 来计算点 p∈ 和 q∈ 之间的最大距离. 求 Disk[{0,0}] 和 Rectangle[{3,3}] 中的点之间的最大距离:
https://wolfram.com/xid/0e7mopp2-ft5pzx
https://wolfram.com/xid/0e7mopp2-l1hdoc
求 Line[{{0,0,0},{1,1,1}}] 和 Ball[{5,5,0},1] 中的点之间的最大距离:
https://wolfram.com/xid/0e7mopp2-ogx39
https://wolfram.com/xid/0e7mopp2-h1n6ry
属性和关系 (4)函数的属性及与其他函数的关联
Maximize 给出最大值,和达到最大值的点:
https://wolfram.com/xid/0e7mopp2-d8jiij
MaxValue 给出目标函数的一个精确的全局最大值:
https://wolfram.com/xid/0e7mopp2-18thy0
https://wolfram.com/xid/0e7mopp2-gro7on
https://wolfram.com/xid/0e7mopp2-3v0yz9
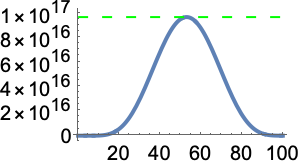
NMaxValue 试图用数值法求出一个全局最大值,但可能求出的是一个局部最大值:
https://wolfram.com/xid/0e7mopp2-51mhiy
https://wolfram.com/xid/0e7mopp2-qtfxil
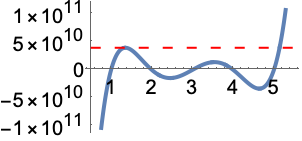
FindMaxValue 求出与起点相关的局部最大值:
https://wolfram.com/xid/0e7mopp2-v7rnoh
https://wolfram.com/xid/0e7mopp2-8rjwjd
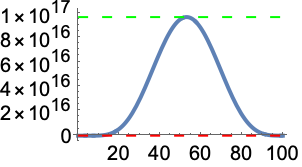
MaxValue 可以求解线性规划问题:
https://wolfram.com/xid/0e7mopp2-mm3mtp
LinearProgramming 可用于求解以矩阵符号形式给出的同一个问题:
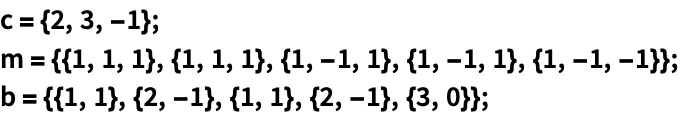
https://wolfram.com/xid/0e7mopp2-i8n5ly
https://wolfram.com/xid/0e7mopp2-b7q2kw
用 RegionBounds 计算边界盒:
https://wolfram.com/xid/0e7mopp2-eqkvxp
https://wolfram.com/xid/0e7mopp2-d4lzah
用 MaxValue 和 MinValue 计算同一个边界盒:
https://wolfram.com/xid/0e7mopp2-cxum90
https://wolfram.com/xid/0e7mopp2-gc4ks2

可能存在的问题 (1)常见隐患和异常行为
MaxValue 要求输入中所有函数是实数值:
https://wolfram.com/xid/0e7mopp2-due48b
https://wolfram.com/xid/0e7mopp2-mnsihk
Wolfram Research (2008),MaxValue,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MaxValue.html (更新于 2021 年).文本
Wolfram Research (2008),MaxValue,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MaxValue.html (更新于 2021 年).
Wolfram Research (2008),MaxValue,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MaxValue.html (更新于 2021 年).CMS
Wolfram 语言. 2008. "MaxValue." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/MaxValue.html.
Wolfram 语言. 2008. "MaxValue." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/MaxValue.html.APA
Wolfram 语言. (2008). MaxValue. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MaxValue.html 年
Wolfram 语言. (2008). MaxValue. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MaxValue.html 年BibTeX
@misc{reference.wolfram_2025_maxvalue, author="Wolfram Research", title="{MaxValue}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/MaxValue.html}", note=[Accessed: 29-March-2025
]}BibLaTeX
@online{reference.wolfram_2025_maxvalue, organization={Wolfram Research}, title={MaxValue}, year={2021}, url={https://reference.wolfram.com/language/ref/MaxValue.html}, note=[Accessed: 29-March-2025
]}