NFractionalD

NFractionalD[f,{x,α},x0]

点 x0における関数 f のリーマン・リウヴィル(Riemann–Liouville)非整数 α 階微分の数値近似を与える．

詳細とオプション

  • NFractionalDは f のリーマン・リウヴィル微積分としても知られるFractionalDの数値版である．
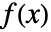  • の 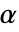階のリーマン・リウヴィル非整数階微分は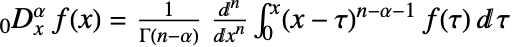として定義される．ただし，n=max(0,TemplateBox[{alpha}, Ceiling])である．
  • NFractionalDはFractionalDによる記号計算が失敗する場合に使われることがある．
  • NFractionalDには次のオプションを使うことができる．
  • Method Automatic使用するメソッド
    AccuracyGoalInfinity目標とする絶対確度の桁数
    PrecisionGoalAutomatic目標精度の桁数
    WorkingPrecisionMachinePrecision内部計算に使用する精度
  • 次は，使用可能なMethodオプションである．
  • Automaticメソッドを自動選択する
    "GrunwaldLetnikov"Grünwald-Letnikov非整数階微積分スキーム
    "RiemannLiouville"リーマン・リウヴィル非整数階微積分スキーム

例題

すべて開くすべて閉じる

例  (5)

二次関数の1/2階微分をある点における x について計算する：

定数の階微分をある点における x について計算する：

指数関数の階微分をプロットする：

任意の点におけるMittagLefflerEの数値非整数階微分：

MittagLefflerE関数の非整数階微分の数値のリストを生成する：

非整数階微分をプロットする：

数値非整数階積分

スコープ  (9)

二乗関数の x についての階微分をプロットする：

Exp関数の0.23階微分の数値計算と記号計算を行う：

任意の点におけるArcTan関数の半階微分の値を計算する：

この関数をプロットする：

Sin関数の階微分：

Sin関数の階積分：

AiryAi関数の半階微分：

BesselJ関数の非整数階微分を数値的に計算する：

MeijerG関数の非整数階微分を数値的に計算する：

三角関数の積の数値計算された非整数階微分と積分をプロットする：

オプション  (2)

Method  (2)

NFractionalDにはリーマン・リウヴィル法とGrünwald–Letnikov法の2つの組込みメソッドがある：

NFractionalDは，Methodが指定されていなければ自動的にリーマン・リウヴィル法を使う：

場合によっては，Grünwald–Letnikov法で数値非整数階微分が計算できる場合がある：

リーマン・リウヴィル法ではこの非整数階微分を計算することはできない：

アプリケーション  (3)

NFractionalDはFractionalDが失敗するときに非整数階微分を数値的に計算することができる：

FractionalDの出力はDifferenceRoot数列を含むことがある：

非整数階微分の特定の階数については，これはHypergeometricPFQ関数の厄介な和である：

しかし，数値計算された非整数階微分のプロットは示唆に富む場合がある：

NFractionalDを使って複素関数の非整数階微分の数値のリストを効率的に生成する：

151個の値の計算に要する時間：

この非整数階微分をプロットする：

特性と関係  (6)

NFractionalDはすべての実数 について定義される：

一般に，定数の非整数階微分は0ではない：

NFractionalDは出力を（MachinePrecisionと指定されていなければ）WorkingPrecisionで与える：

NFractionalDはMethodオプションが指定されていなければ"RiemannLiouville"法を使う：

数値的なNFractionalDアプローチを使って非整数階微分をプロットする：

記号的なFractionalDアプローチと比較する：

NCaputoDは負の階 についてはNFractionalDと一致する：

考えられる問題  (3)

Methodが正しくなければNFractionalDはエラーメッセージを生成する：

入力精度がWorkingPrecisionより低ければ，NFractionalDはエラーメッセージを生成する：

NFractionalDは評価点として数値しか取らない：

おもしろい例題  (1)

Sin関数とその半階，1階，階微分をプロットする：

Wolfram Research (2022), NFractionalD, Wolfram言語関数， https://reference.wolfram.com/language/ref/NFractionalD.html.

テキスト

Wolfram Research (2022), NFractionalD, Wolfram言語関数， https://reference.wolfram.com/language/ref/NFractionalD.html.

CMS

Wolfram Language. 2022. "NFractionalD." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NFractionalD.html.

APA

Wolfram Language. (2022). NFractionalD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NFractionalD.html

BibTeX

@misc{reference.wolfram_2024_nfractionald, author="Wolfram Research", title="{NFractionalD}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/NFractionalD.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_nfractionald, organization={Wolfram Research}, title={NFractionalD}, year={2022}, url={https://reference.wolfram.com/language/ref/NFractionalD.html}, note=[Accessed: 21-November-2024 ]}