NFractionalD
NFractionalD[f,{x,α},x0]
给出函数 f 在点 x0 处的 α 阶黎曼–刘维尔分数阶导数 ![]() 的数值近似.
的数值近似.
更多信息和选项

- NFractionalD 是 FractionalD 的数值化版本,亦称为 f 的 Riemann–Liouville 微分积分.
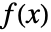 的
的 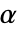 阶 Riemann–Liouville 分数导数被定义为
阶 Riemann–Liouville 分数导数被定义为 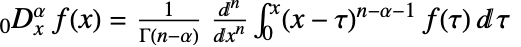 ,其中
,其中 ![n=max(0,TemplateBox[{alpha}, Ceiling]) n=max(0,TemplateBox[{alpha}, Ceiling])](Files/NFractionalD.zh/5.png) .
. - NFractionalD 通常在用 FractionalD 进行符号计算失败的情况下使用.
- 可对 NFractionalD 给出以下选项:
-
Method Automatic 要使用的方法 AccuracyGoal Infinity 追求的绝对准确度的位数 PrecisionGoal Automatic 追求的精度的位数 WorkingPrecision MachinePrecision 内部计算使用的精度 - 可使用以下 Method 选项设置:
-
Automatic 自动选择方法 "GrunwaldLetnikov" Grünwald-Letnikov 分数阶微分积分方法 "RiemannLiouville" Riemann-Liouville 分数阶微分积分方法
范例
打开所有单元关闭所有单元基本范例 (5)
MittagLefflerE 在一个点上的数值分数导数:
生成 MittagLefflerE 函数的分数阶导数的数值列表:
范围 (9)
选项 (2)
Method (2)
NFractionalD 有两个内置的方法,Riemann–Liouville 和 Grünwald–Letnikov 方法:
如果没有指定 Method,NFractionalD 自动使用 Riemann–Liouville 方法:
应用 (3)
当 FractionalD 失败时,NFractionalD 能够计算分数阶导数的数值结果:
FractionalD 输出可能含有 DifferenceRoot 序列:
对于特定阶数的分数微分,以下结果含有 HypergeometricPFQ 函数的冗长求和:
用 NFractionalD 高效生成复变函数的分数阶导数的数值列表:
属性和关系 (6)
NFractionalD 对所有实数 ![]() 有定义:
有定义:
NFractionalD 给出的结果的精度为 WorkingPrecision(如果没有指定,则为 MachinePrecision):
如果没有指定 Method 选项,NFractionalD 使用 "RiemannLiouville" 方法:
用 NFractionalD 绘制分数阶导数:
与使用 FractionalD 符号计算所得的结果相比较:
对于负的阶数 ![]() ,NCaputoD 与 NFractionalD 的结果一致:
,NCaputoD 与 NFractionalD 的结果一致:
可能存在的问题 (3)
如果 Method 选项不正确,NFractionalD 将生成一条出错消息:
如果输入精度小于 WorkingPrecision,NFractionalD 将生成一条出错消息:
NFractionalD 只接受用数字给出的点:
巧妙范例 (1)
绘制 Sin 函数以及它的半阶、一阶和 ![]() 阶导数:
阶导数:
文本
Wolfram Research (2022),NFractionalD,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NFractionalD.html.
CMS
Wolfram 语言. 2022. "NFractionalD." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/NFractionalD.html.
APA
Wolfram 语言. (2022). NFractionalD. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NFractionalD.html 年