Perimeter
Perimeter[reg]
二次元領域 reg の周長を与える.
Perimeter[{x1,x2},{s,smin,smax},{t,tmin,tmax}]
デカルト座標 xiが s と t の関数であるパラメータ化された領域の周長を与える.
Perimeter[{x1,x2},{s,smin,smax},{t,tmin,tmax},chart]
xiを指定された座標チャートの座標として解釈する.
詳細とオプション
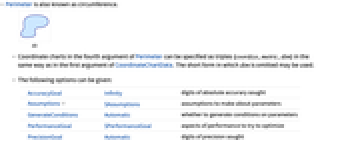
- Perimeterは外周としても知られている.
- Perimeterの第4引数内の座標チャートは,CoordinateChartDataの第1引数におけるのと同じように{coordsys,metric,dim}として指定することができる.dim が省略された短縮形も使うことができる.
- 次は使用可能なオプションである.
-
AccuracyGoal Infinity 目標とする絶対確度の桁数 Assumptions $Assumptions 周長について行う仮定 GenerateConditions Automatic パラメータについての条件を生成するかどうか PerformanceGoal $PerformanceGoal パフォーマンスのどの局面について最適化するか PrecisionGoal Automatic 目標とする精度の桁数 WorkingPrecision Automatic 内部計算に使用する精度 - Perimeterは,GeometricSceneの記号領域と一緒に使うことができる.

例題
すべて開くすべて閉じるスコープ (14)
数式定義領域 (4)
メッシュ領域 (3)
派生領域 (2)
オプション (2)
WorkingPrecision (1)
機械演算でPerimeterを計算する:
アプリケーション (4)
正五角形の40.5エーカーの土地を持つ農家がある.この土地を囲むのにはどのくらいの長さの柵が必要だろうか.
土地を,半径が未知であるRegularPolygonとしてモデル化する:
[0,1]×[0,1]内のMengerMeshの周長を求める:
次数 n のMengerMeshの周長についての一般公式を求める:
領域が[0,1]×[0,1]の境界内にあっても,周長は無限大に近付く:
海岸線のパラドックスには,国の国境は事実上フラクタルであり,したがってその周長は無限であるとある [詳細].
特性と関係 (3)
全次元の成分しかない領域については,周長はその境界のArcLengthである:
非零の周長を持つ領域のAreaは非零である:
ラミナ(ユークリッド平面内の二次元閉領域)実体の周長を求める:
EntityValueを使って外半径が5で内半径が1のサリノンの周長を求める:
テキスト
Wolfram Research (2017), Perimeter, Wolfram言語関数, https://reference.wolfram.com/language/ref/Perimeter.html (2019年に更新).
CMS
Wolfram Language. 2017. "Perimeter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Perimeter.html.
APA
Wolfram Language. (2017). Perimeter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Perimeter.html