PointCountDistribution

PointCountDistribution[pproc,reg]

領域 reg における点過程 pproc についての点の数の分布を表す．

PointCountDistribution[pproc,{reg1,…,regn}]

領域 regiにおける点の数の結合分布を表す．

詳細

  • PointCountDistributionは点数分布としても知られている．
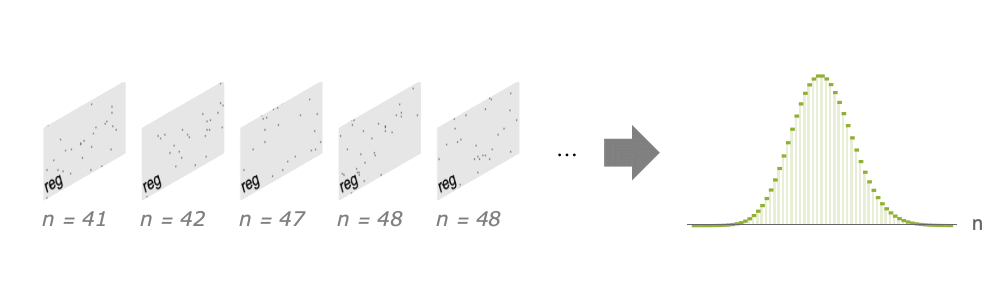
  • PointCountDistributionは，点過程 pproc の結果としての点パターンにおける点の数の分布である．
  • PointCountDistributionは，森の木の数，サンプル中のセル数，表面の傷の数のような，観測における点の総数の推定によく使われる．
  • 点過程 pproc について，全次元 reg の領域における点の数は，分布がPointCountDistribution[pproc,reg]によって表される確率変数である．
  • PointCountDistribution[pproc,reg]の平均は，領域 reg における点過程 pproc の平均測度である．
  • 領域 regiおよび reg は，SpatialObservationRegionQで試されるように全次元かつ有界でなければならないが，特別な場合はパラメータで定義することができる．
  • PointCountDistributionは，可能な場合は常に，既知の特殊分布に簡約される．
  • PointCountDistributionは，Mean，CDF，RandomVariate等の関数と一緒に使うことができる．

例題

すべて開くすべて閉じる

例  (3)

単位円板上のPoissonPointProcessについての点の数の分布：

点の数の平均と分散を求める：

単位球上のHardcorePointProcessについてのPointCountDistribution：

分布のシミュレーションを行う：

GeoDiskについてのPointCountDistribution：

スコープ  (4)

単位円板上のBinomialPointProcessについてのPointCountDistribution：

下位領域の点の数の分布：

点の平均数を計算する：

単位円板上のInhomogeneousPoissonPointProcessのPointCountDistribution：

互いに素な2つの領域の和集合上で：

シミュレーションを行う：

交差する2つの領域上で：

シミュレーションを行う：

平均：

Neyman–Scottタイプのクラスタ過程についてのPointCountDistributionはCompoundPoissonDistributionである：

コーシー(Cauchy)点過程：

Matérn点過程：

Thomas点過程：

分散ガンマ点過程：

一般に，Neyman–Scott点過程の点の数の分布はクラスタ点の空間分布には依存しない：

PointCountDistributionの閉じた形がない場合に確率と推定値を計算する：

シミュレーションを使って平均を計算する：

シミュレーションを使って事象確率を計算する：

アプリケーション  (5)

Strauss点過程について，単位円板内の点の平均数を計算する：

合板の欠陥が50平方フィートあたり平均1つ発生するとする．1平方フィートごとに欠陥を見付ける過程のシミュレーションを行う：

与えられた領域内の欠陥数：

4フィート x 8フィートの板に欠陥がない確率を求める：

面積が7.54cm^2の丸い鏡に欠陥がない確率は0.91である．同じ研磨プロセスを使用して19.50cm^2の面積を持つ別の丸い鏡を製造する．欠陥が独立していてランダムに配置されていると仮定して，大きな鏡に欠陥がない確率を求める：

鏡の欠陥数の分布：

欠陥点過程の強度を求める：

2番目の鏡の欠陥数の分布：

大きい鏡に欠陥がない確率：

1920×1080画素のLCDディスプレイがある．欠陥がある画素が15個以下の場合，ディスプレイは受領される．生産によって画素に欠陥が生じる確率はであり，欠陥がある画素位置は独立でランダムである．受領されるディスプレイの割合を求める：

欠陥画素の配置のシミュレーションを行う：

ディスプレイにおける欠陥画素数の分布：

ディスプレイの欠陥画素が15以下である確率を求める：

4000×2000画素のディスプレイを作成する際に，少なくとも90％の受領率を維持するために必要な画素欠陥率を求める：

受領率を画素欠陥率の関数としてプロットする：

受領可能な最大画素欠陥率を求める：

結果を確かめる：

シカゴにおける自動車関連盗難事件数：

この強度の同次ポアソン過程を定義する：

事件の平均数を求める：

事件数が1200未満になる確率を求める：

郵便番号60639における事件数の期待値を計算する：

特性と関係  (4)

ペアごとの離散領域上でのPointCountDistributionはProductDistributionである：

各領域上のPointCountDistribution：

領域のリスト上の多変量PointCountDistribution：

重なり合う領域上のPointCountDistribution：

各領域上のPointCountDistribution：

領域のリスト上の多変量PointCountDistribution：

領域が交差しているところでは成分が相関している：

BinomialPointProcessを覆う領域全体についてのPointCountDistribution：

3集合被覆を定義する：

被覆の点数分布：

非数値パラメータがある領域についてのPointCountDistribution：

Wolfram Research (2020), PointCountDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/PointCountDistribution.html.

テキスト

Wolfram Research (2020), PointCountDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/PointCountDistribution.html.

CMS

Wolfram Language. 2020. "PointCountDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PointCountDistribution.html.

APA

Wolfram Language. (2020). PointCountDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PointCountDistribution.html

BibTeX

@misc{reference.wolfram_2024_pointcountdistribution, author="Wolfram Research", title="{PointCountDistribution}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/PointCountDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_pointcountdistribution, organization={Wolfram Research}, title={PointCountDistribution}, year={2020}, url={https://reference.wolfram.com/language/ref/PointCountDistribution.html}, note=[Accessed: 21-November-2024 ]}