Polygon

Polygon[{p1,…,pn}]

表示一个顶点为 pi 的填充多边形.

Polygon[{p1,…,pn}{{q1,…,qm},…}]

表示一个多边形，其中洞为 {q1,…,qm},….

Polygon[{poly1,poly2,…}]

表示多个多边形 polyi.

Polygon[{p1,…,pn},data]

表示一个多边形，其中坐标是 data 中的整数 i，被接受为 pi.

更多信息和选项

  • Polygon 可被用作几何区域及图形基元.
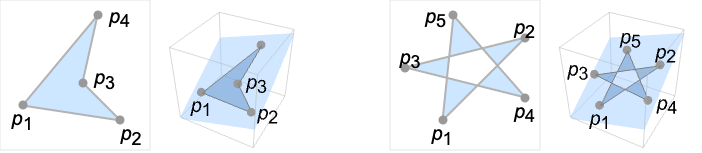
  • Polygon[{p1,…,pn}] 是一个平面区域，表示所有的点在闭合曲线中，线段为 {p1,p2},…,{pn-1,pn} 和 {pn,p1}.
  • 如果来自于平面中任何方向的点的射线穿过边界线段奇数次，那么点是多边形的一个元素.
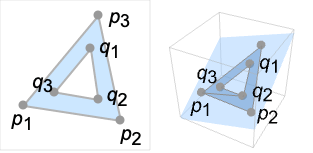
  • Polygon[{p1,…,pn}{{q1,…,qm},…}] 指定带有洞的多边形包含外多边形 Polygon[{p1,…,pn}] 和一个或多个内多边形 Polygon[{q1,…,qm}],….
  • 如果在外多边形，不在任何内多边形，那么点是多边形的一个元素.
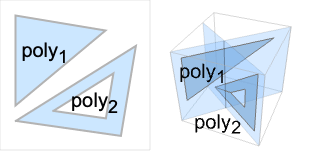
  • Polygon[{poly1,poly2,…}] 是有洞和无洞多边形 polyi 的集合，被视为几何计算的 polyi 并集.
  • Polygon[{p1,…,pn},data] 有效地用对应的 pi 替代作为 data 中坐标的整数 i.
  • Polygon[{p1,…,pn},{b1,…,bn}]多边形边界点 {pb1,…,pbk}
    Polygon[{p1,…,pn},{{o1,…,ok}{{i1,…,il},…}]外多边形边界点 {po1,…,pok} 和内多边形边界 {pi1,…,pil} 等
    Polygon[{p1,…,pn},{{b1,…,bn},{o1,…,ok}{{i1,…,il},…},…}]多个多边形的集合
  • 在几何区域中，点 pi 可以有任何嵌入维度，但是必须位于平面内并有同样的嵌入维度.
  • 在图形中，点 pi 可以是 Scaled、Offset、ImageScaled 和 Dynamic 表达式.
  • 有些指令，比如 FaceForm、EdgeForm、Texture、Specularity、Opacity 和着色会影响图形渲染.
  • FaceForm[front,back] 可用来指定多边形在三维中前面和后面的不同样式. 由右手规则和前三个点的方向定义前面.
  • 在图形中可以使用下列选项和设置：
  • VertexColors Automatic进行插值着色时顶点的颜色
    VertexNormals Automatic显示明暗度用的有效顶点法线
    VertexTextureCoordinates None显示纹理时使用的坐标
  • Polygon 可用于 GeometricScene 内的符号点.

范例

打开所有单元关闭所有单元

基本范例  (2)

多边形：

图形图像：

面积：

不同样式的三维多边形：

范围  (21)

图形  (11)

规范  (2)

多个多边形：

有多个顶点的多边形：

样式  (6)

颜色指令可以指定多边形的表面颜色：

Texture 可以用于指定多面体表面的纹理：

Texture 可以与不同的 Opacity 一起工作：

Texture 可以与不同的 Lighting 一起工作：

FaceForm 和 EdgeForm 可以用来指定内部和边界的样式：

在三维图形中，可以使用 FaceForm 指定前面和后面的不同属性:

使用 FaceForm 在三维图像中设置前后不同的纹理：

可以用 VertexColors 指定顶点的颜色：

在三维多边形中， 可以用 VertexNormals 来指定顶点法线：

  (3)坐标

用 Scaled 坐标：

在二维空间中用 ImageScaled 坐标：

在二维空间中，用 Offset 坐标：

区域  (10)

嵌入维度：

几何维度：

判断某点是否为该区域的成员：

获取成为该区域成员的条件：

面积：

几何中心：

距一个点的距离：

图示：

距一个点的有符号距离：

图示：

区域中最近的点：

最近的点：

多边形是有界的：

获取范围：

在多边形上 Integrate：

在多边形上最优化：

在多边形上解方程：

选项  (7)

VertexColors  (2)

顶点着色的多边形：

指定三维多边形的顶点颜色：

VertexNormals  (1)

用边向量的向量积来计算法向量：

法向方向指向 {1,-1,1} 的三角：

用不同的法向量来影响阴影：

VertexTextureCoordinates  (4)

纹理映射多边形：

纹理映射为二维多面体：

纹理映射为三维多面体：

通过使用非统一标准的纹理坐标值重复纹理：

VertexColors 优先于纹理映射：

应用  (3)

定义有 个顶点的多边形：

正则多边形：

星状多边形：

定义正六角形：

正则六角形的砖：

从 PolyhedronData 获得面多边形：

相对于图心来缩短每个面：

属性和关系  (4)

GraphicsComplex 提供一个有效的方式来产生多个有共享顶点的多边形：

将 Normal 应用到图形组合中产生普通的多边形：

Polygon 是 Triangle 的泛化：

Polygon 是 Rectangle 的泛化：

三个顶点的 Simplex 是 Polygon 的特例：

可用于二维以上的任意维度：

可能存在的问题  (3)

在三维空间中，如果一个顶点不在一个平面内，多边形三角是不可预测的：

退化多边形不是有效的几何区域：

在单个多边形间的缝作为反走样的结果：

用单个多边形对象来避免任何缝：

巧妙范例  (3)

一组随意排列的三角形：

数字花瓣：

旋转的星：

Wolfram Research (1988)，Polygon，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Polygon.html （更新于 2019 年）.

文本

Wolfram Research (1988)，Polygon，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Polygon.html （更新于 2019 年）.

CMS

Wolfram 语言. 1988. "Polygon." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/Polygon.html.

APA

Wolfram 语言. (1988). Polygon. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Polygon.html 年

BibTeX

@misc{reference.wolfram_2024_polygon, author="Wolfram Research", title="{Polygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Polygon.html}", note=[Accessed: 15-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_polygon, organization={Wolfram Research}, title={Polygon}, year={2019}, url={https://reference.wolfram.com/language/ref/Polygon.html}, note=[Accessed: 15-November-2024 ]}