PositiveSemidefiniteMatrixQCopy to clipboard.
✖
PositiveSemidefiniteMatrixQ
范例
打开所有单元关闭所有单元基本范例 (2)常见实例总结
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-k5tb4m
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-1iqf8o
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-gntl81
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-0bvue1
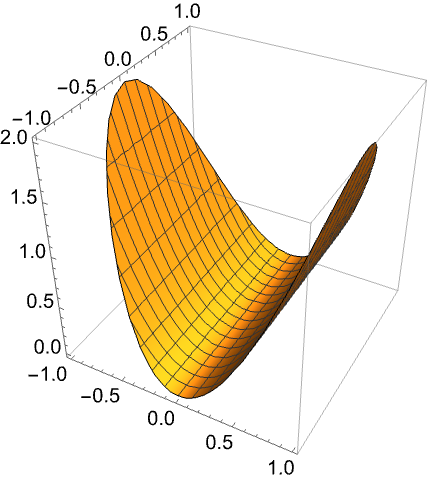

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-znfdke
范围 (10)标准用法实例范围调查
基本用法 (6)
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-1kq4tu
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-5fazgj

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-tfdinn
用 PositiveSemidefiniteMatrixQ 测试任意精度的矩阵:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-eoeqf9

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-ow584e
用 PositiveSemidefiniteMatrixQ 测试符号矩阵:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-62ooyj
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-rni58c
PositiveSemidefiniteMatrixQ 可高效处理大型数值矩阵:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-1gk6wb
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-c5kyvx
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-nb2gv9
特殊矩阵 (4)
用 PositiveSemidefiniteMatrixQ 测试稀疏矩阵:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-0lcs36
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-cvjhfs
用 PositiveSemidefiniteMatrixQ 测试结构矩阵:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-my6pw
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-n6jq9t
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-tpv6mn
HilbertMatrix 是半正定矩阵:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-slp5k9
选项 (1)各选项的常用值和功能
Tolerance (1)
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-35lu76
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-mrsvrl
调整选项 Tolerance 接受矩阵作为半正定矩阵:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-cbjh4n
应用 (13)用该函数可以解决的问题范例
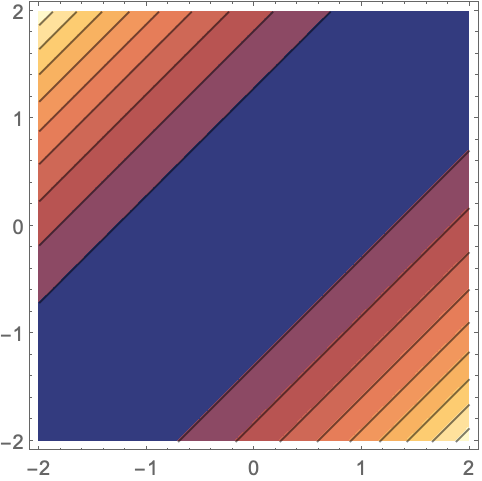
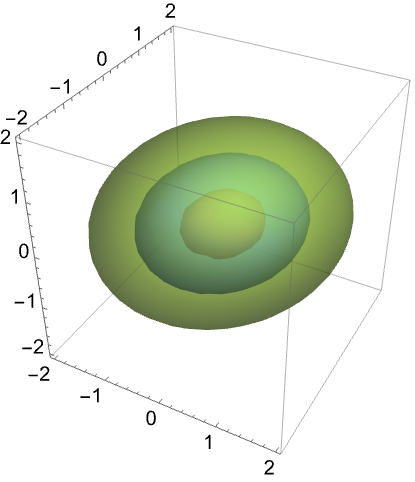
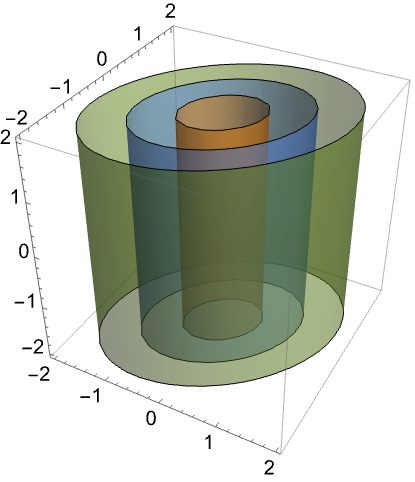
半正定矩阵的几何与代数性质 (5)
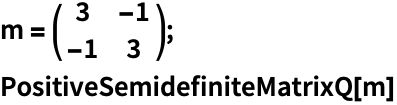
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-xq3amu
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-7eaz20
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-2bl8ys
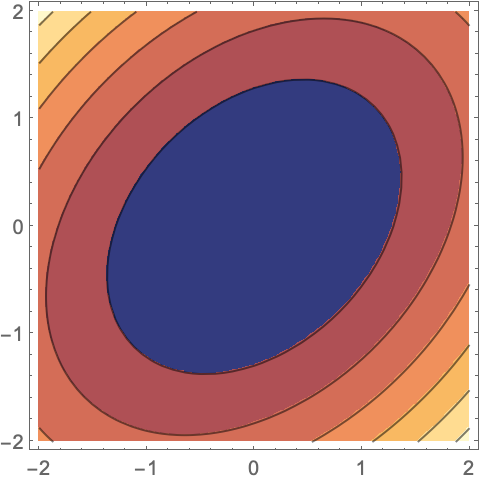

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-mw6kb
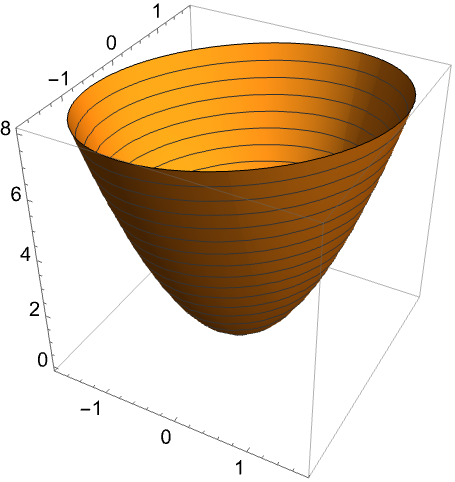
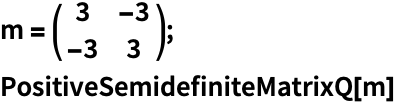
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-z3oc9l
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-77xx63
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-589e5j

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-upvrmb
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-e6yjz3
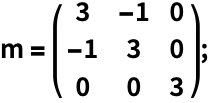
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-lrsik1
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-xutlb2
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-zxn0wi

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-i4nhjp
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-4fnyml
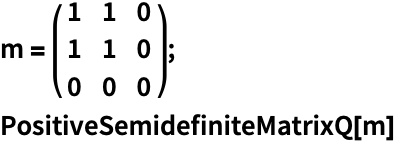
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-1b2grz
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-x0igid

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-t4honb
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-8p80us
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-wvuonx
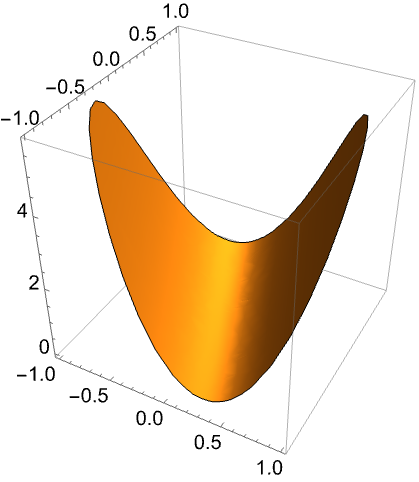
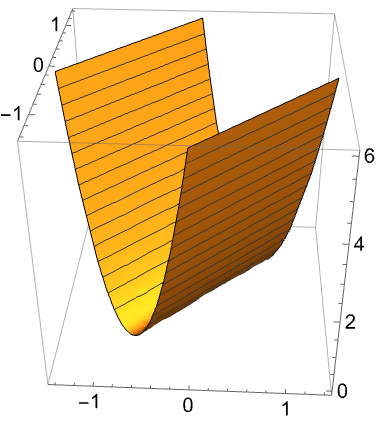
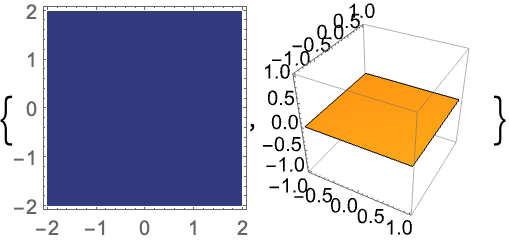
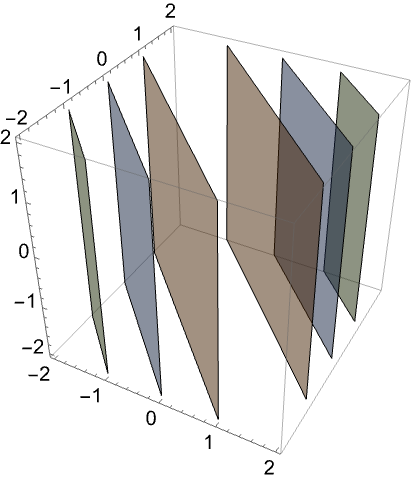
对于实值矩阵 ![]() ,只有对称的部分决定
,只有对称的部分决定 ![]() 是否为半正定矩阵. 写为
是否为半正定矩阵. 写为 ![]() ,
,![]() 为对称部分,
为对称部分,![]() 为非对称部分:
为非对称部分:
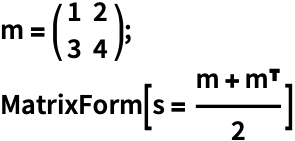
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-343mgv
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-i3xo0f
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-w3jv4l
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-jf2jdt
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-ri3cbu
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-cg0348
对于复矩阵 ![]() ,只有 Hermitian 部分决定
,只有 Hermitian 部分决定 ![]() 是否为半正定矩阵. 写为
是否为半正定矩阵. 写为 ![]() ,
,![]() 是 Hermitian 矩阵,
是 Hermitian 矩阵,![]() 为反埃尔米特矩阵:
为反埃尔米特矩阵:
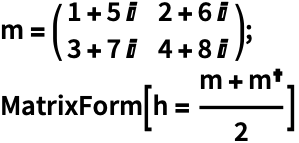
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-7in8hm
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-tq6566
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-1i72sc
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-33o78l
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-ww36rj
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-7zx7p2
半正定矩阵的来源 (8)
实 Covariance 矩阵总是对称的和半正定的:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-r24rp8
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-z9e7k3
![]() 为方阵,计算 SingularValueDecomposition[m]:
为方阵,计算 SingularValueDecomposition[m]:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-ugfzlm
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-pu6p09

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-q5c30y
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-ernk9
从 WishartMatrixDistribution 得到的矩阵是实对称半正定矩阵:

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-gf7yyg
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-0bx5p8
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-4r8vsp
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-coq2u3
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-d9orwc
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-co29v5
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-11h6uz
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-dr1ppf
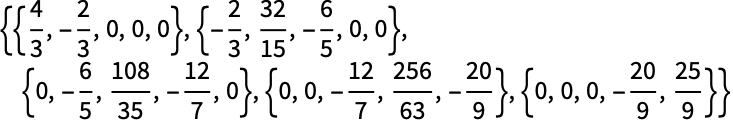
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-hpm29l
矩阵 Min[i,j] 一定是对称半正定矩阵:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-r3v5d2
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-uj576h
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-wpbkgs
属性和关系 (13)函数的属性及与其他函数的关联
对于任何不是矩阵的 x,PositiveSemidefiniteMatrixQ[x] 返回 False:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-52egbw
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-uc2nl4
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-4rtpxr
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-0aaw2u
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-5s7mky
当且仅当实矩阵的对称部分是半正定的,实矩阵 ![]() 才是半正定矩阵:
才是半正定矩阵:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-gur7yw
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-32pn0w
一般情况下,当且仅当矩阵的 Hermitian 部分是半正定的,矩阵 ![]() 才是半正定矩阵:
才是半正定矩阵:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-1woht6
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-v0nw29
当且仅当实对称矩阵的特征值都是非负的,实对称矩阵才是半正定矩阵:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-0gbqgh
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-odzxnu
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-mi6tly
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-gegyod
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-olr87h
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-2wlag4
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-pnkm16
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-i7vtvh
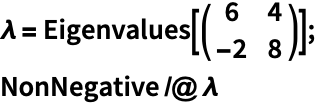
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-pordaa
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-ymsd52
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-wktjrm

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-6i3wqm

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-5cykp8
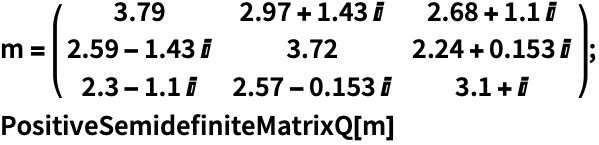
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-5mtsrr
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-1lhk03
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-ros799
根据谱定理,可用 JordanDecomposition 将 ![]() 酉对角化:
酉对角化:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-5xk4eo
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-e7l3ru
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-uu247o
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-s4ntwc

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-6c25gj
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-hrrwad
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-umljb8
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-qr2db6
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-umgbzb
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-ubfv0t
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-svo4k1
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-wm94q3
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-6g4zxu
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-unnzjp
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-1mwrnq
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-gn4gq1
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-6qsx6k

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-h57z2p
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-pjy0vj
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-cicqaf
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-f456sv
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-2pmo1x

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-0zjggt
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-8z4qk6
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-7bxtuv

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-xgm4wo
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-d8y78b
两个对称半正定矩阵的 Kronecker 积是对称半正定矩阵:

https://wolfram.com/xid/0bhf3wgupbucv1cods4z-luvzz6
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-nhifmq
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-78dgkz
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-95pre
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-bi9dt6
可能存在的问题 (2)常见隐患和异常行为
CholeskyDecomposition 不用于对称或者奇异的 Hermitian 半正定矩阵:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-eap5hh
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-fh02j4
PositiveSemidefiniteMatrixQ 将给出 False,除非它可以证明一个符号矩阵是半正定的:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-mht1w7
同时使用 Eigenvalues 和 Reduce 可给出更精确的结果:
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-0dkk5z
https://wolfram.com/xid/0bhf3wgupbucv1cods4z-jri0ni
Wolfram Research (2014),PositiveSemidefiniteMatrixQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PositiveSemidefiniteMatrixQ.html.文本
Wolfram Research (2014),PositiveSemidefiniteMatrixQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PositiveSemidefiniteMatrixQ.html.
Wolfram Research (2014),PositiveSemidefiniteMatrixQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PositiveSemidefiniteMatrixQ.html.CMS
Wolfram 语言. 2014. "PositiveSemidefiniteMatrixQ." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/PositiveSemidefiniteMatrixQ.html.
Wolfram 语言. 2014. "PositiveSemidefiniteMatrixQ." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/PositiveSemidefiniteMatrixQ.html.APA
Wolfram 语言. (2014). PositiveSemidefiniteMatrixQ. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PositiveSemidefiniteMatrixQ.html 年
Wolfram 语言. (2014). PositiveSemidefiniteMatrixQ. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PositiveSemidefiniteMatrixQ.html 年BibTeX
@misc{reference.wolfram_2025_positivesemidefinitematrixq, author="Wolfram Research", title="{PositiveSemidefiniteMatrixQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/PositiveSemidefiniteMatrixQ.html}", note=[Accessed: 30-March-2025
]}BibLaTeX
@online{reference.wolfram_2025_positivesemidefinitematrixq, organization={Wolfram Research}, title={PositiveSemidefiniteMatrixQ}, year={2014}, url={https://reference.wolfram.com/language/ref/PositiveSemidefiniteMatrixQ.html}, note=[Accessed: 30-March-2025
]}