Probability[pred,xdist]
x が確率分布 dist に従うという仮定の下で述語 pred を満足する事象の確率を与える.
Probability[pred,xdata]
x が data によって与えられた確率分布に従うという仮定の下で述語 pred を満足する事象の確率を与える.
Probability[pred,{x1,x2,…}dist]
{x1,x2,…}が多変量分布 dist に従うという仮定の下で事象が pred を満足する確率を与える.
Probability[pred,{x1dist1,x2dist2,…}]
x1, x2, …が独立であり分布 dist1, dist2, …に従うという仮定の下で事象が pred を満足する確率を与える.
Probability[pred1pred2,…]
pred2を仮定して pred1の条件付き確率を与える.




Probability
Probability[pred,xdist]
x が確率分布 dist に従うという仮定の下で述語 pred を満足する事象の確率を与える.
Probability[pred,xdata]
x が data によって与えられた確率分布に従うという仮定の下で述語 pred を満足する事象の確率を与える.
Probability[pred,{x1,x2,…}dist]
{x1,x2,…}が多変量分布 dist に従うという仮定の下で事象が pred を満足する確率を与える.
Probability[pred,{x1dist1,x2dist2,…}]
x1, x2, …が独立であり分布 dist1, dist2, …に従うという仮定の下で事象が pred を満足する確率を与える.
Probability[pred1pred2,…]
pred2を仮定して pred1の条件付き確率を与える.
詳細とオプション

- xdist は x
 dist
dist dist または x\[Distributed]dist と入力できる.
dist または x\[Distributed]dist と入力できる. - pred1pred2は pred1
 cond
cond pred2 または pred1\[Conditioned]pred2と入力できる.
pred2 または pred1\[Conditioned]pred2と入力できる. - 連続分布 dist では,pred の確率は ∫Boole[pred]f[x]x で与えられる.ただし,f[x]は dist の確率密度関数であり,積分は dist の領域で行われるものとする.
- 離散分布 dist では,pred の確率は ∑Boole[pred]f[x]で与えられる.ただし,f[x]は dist の確率密度関数であり,総和は dist の領域で行われるものとする.
- データ集合 data では,pred の確率はSum[Boole[pred],{x,data}]/Length[data]で与えられる.
- 一変量データは値のリスト{v1,v2,…}として,多変量データはベクトルのリスト{{v11,…,v1m},{v21,…,v2m},…}として与えられる.
- Probability[pred,{x1dist1,x2dist2}]はExpectation[Probability[pred,x2dist2],x1dist1]に対応するので,最後の変数が最初に合計されたり積分されたりする.
- N[Probability[…]]は記号的に求まらない確率についてはNProbabilityを呼び出す. »
- 使用可能なオプション
-
Assumptions $Assumptions パラメータについての仮定 » GenerateConditions False パラメータについての条件を生成するかどうか Method Automatic 使用するメソッド »
予備知識
- Probability[pred,x]は,選ばれた確率変数 x が指定された確率分布に従う(つまり, はNormalDistribution,BinomialDistribution,ChiSquareDistribution等の連続分布あるいは離散分布である),あるいは,指定されたデータ集合から取られる( つまり, はデータ集合を定義する)という仮定の下で述語 pred を満足する事象の確率を表す. はDistributedの短縮表記である.Probabilityの出力
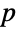 は,
は,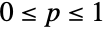 の数(不可能な事象の確率は0であり,確実な事象の確率は1である),あるいは入力パラメータを含む記号式である.
の数(不可能な事象の確率は0であり,確実な事象の確率は1である),あるいは入力パラメータを含む記号式である. - Probabilityは,多変量分布,EmpiricalDistribution,HistogramDistribution,KernelMixtureDistributionのようなノンパラメトリック分布,TransformedDistribution,ProductDistributionのような派生分布にも使うこともできる.さらに,Probabilityは,ContinuousMarkovProcess,DiscreteMarkovProcess,WienerProcess,PoissonProcess等で定義されるものを含むランダム過程にも適用することができる.
- 述語 pred は,線形と非線形両方の不等式や不等式の論理結合を含むことができる.Probabilityは,pred1pred2の形式の述語を使って条件付きの確率を計算することができる.ただし, はConditionedの短縮表記である.Probabilityには,Assumptions,GenerateConditions,Methodを含む数多くのオプションを渡すことができる.Probabilityが与える出力は,記号積分や総和等の厳密メソッドを使って計算される.数値メソッドを含む,これに対応する結果は,NProbabilityで得ることができる.
- PDF,CDF,SurvivalFunctionを含むWolfram言語関数のいくつかは,特定の述語構造を持つProbabilityを使って得られる結果と等しいものを返す.さらに,Probabilityによって得られた結果は,ExpectationとBoole構造を対にすることで,Expectationによっても得られることがある.例えば,Expectation[Boole[1<x<3],xNormalDistribution[]]はProbability[1<x<3,xNormalDistribution[]]に等しい.
- Probabilityを使って確率の多くの問題を厳密に解くことができる.例えば,2個のサイコロを投げて目の合計が3あるいは4になる確率は,Probability[3≤x+y≤4,{x,y}DiscreteUniformDistribution[{{1,6},{1,6}}]]で得られ,3つ1組になった一様分布に従う確率変数
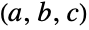 が
が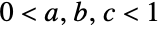 を満足する確率は,多項式
を満足する確率は,多項式 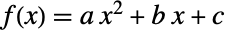 を与える.実根はProbability[b2-4a c≥0,{a,b,c}UniformDistribution[Table[{0,1},{3}]]]で計算することができる.
を与える.実根はProbability[b2-4a c≥0,{a,b,c}UniformDistribution[Table[{0,1},{3}]]]で計算することができる.
例題
すべて開く すべて閉じるスコープ (30)
基本的な用法 (9)
記号評価が失敗した場合には,NProbabilityを呼び出すためにN[Probability[…]]を適用する:
Assumptionsがない場合は条件が生成される:
Assumptionsがある場合は,与えられた仮定の下で有効な結果が返される:
数量の使用 (3)
ノンパラメトリック分布 (4)
一変量EmpiricalDistributionを使って確率を計算する:
一変量HistogramDistributionを使う:
一変量KernelMixtureDistributionを使う:
打ち切られたデータをSurvivalDistributionと一緒に使う:
派生分布 (9)
TransformedDistributionを使って確率を計算する:
ProductDistributionを使って確率を求める:
オプション (5)
Assumptions (1)
Assumptionsがないと,条件が生成される:
Assumptionsがあると,その条件下で有効な結果が返される:
Method (4)
計算された確率は2つのCDF評価の差として与えられる:
ここでは,述語が超越的なので累積分布関数法はうまくいかない:
TukeyLambdaDistributionに従う事象の確率を計算する:
以下では分布の確率密度関数が閉形式では求まらないのでQuantileを使っている:
この例はIntegrateを使う:
Activateを使って結果を計算する:
アプリケーション (50)
ランダムな実験 (8)
コイントスの実験は表が出るまで公正なコインを何度も投げ上げるものである.このプロセスのシミュレーションを行う:
公正なコインを n 回トスした場合に表が出る回数はBinomialDistributionでモデル化できる:
100回コイントスをした場合に60回から80回表が出る確率を計算する:
公正な六面のサイコロはDiscreteUniformDistributionを使ってモデル化することができる:
3個のサイコロを無作為にここでは![]() 回投げる様子を生成して証明する:
回投げる様子を生成して証明する:
ある壷に100個の要素が入っていて,そのうち40個が特別だとする:
50回要素を取り出した場合に25個より多くが特別である確率を計算する:
スポーツとゲーム (4)
チェス名人のガルリ・カスパロフはチェスの試合で同時に100人のアマチュアを相手してにチェスを行う.このようなゲームで彼が負ける率は1%だと推定される.彼が負けない,あるいは2,5,10ゲーム負ける確率を求める:
彼が負ける確率が10%となるような,より強い相手5人とゲームを行っている場合について同じ計算をする:
フリースローの成功率が0.75のバスケット選手がいる.10回のフリースローのシミュレーションを行う:
この選手が試合で3回のフリースローのうち2回に成功する確率を求める:
クラップス[MathWorld]では,2個のサイコロが投げられる:
「スネークアイ(両方が1)」[MathWorld]が出る確率を求める:
「ボックスカー(両方が6)」[MathWorld]が出る確率:
「eighter from Decatur(合計で8の目)」[MathWorld]が出る確率:
「リトルジョー(合計で4の目)」[MathWorld]が出る確率:
保険数理 (5)
ある保険数理士が,保険契約者で2回保険を請求する人は4回請求する人の3倍になることを発見した.請求された保険件数がポアソン(Poisson)分布に従うものとして,請求された保険件数の分散を求める:
小さい会社の従業員の医療費保険金の支払い請求を取り扱う団体保険がある.1年に請求される値 ![]() は
は ![]() で表される.ただし,
で表される.ただし,![]() は密度関数が
は密度関数が![]() で
で![]() に比例する確率変数である.
に比例する確率変数である.![]() が1万を超えるとして,
が1万を超えるとして,![]() が4万を超える条件付き確率を求める:
が4万を超える条件付き確率を求める:
大企業の保険の入札に2つの保険会社が参加する.入札額は2000から2200の間でなければならない.入札額の違いが20以上の場合は額の低い方が選ばれる.入札額の違いが20未満の場合には,入札業者の両方についてさらに検討が加えられる.2つの入札が独立で両方とも2000から2200の間で一様分布に従うと仮定し,両業者がさらに検討される確率を求める:
自動車保険の支払い請求は平均$19,400,標準偏差$5,000で正規分布に従う.無作為に選んだ25件の支払い請求の平均が$20,000を超える確率を求める:
よいドライバーと悪いドライバーからの最初の保険金支払い請求までの時間は互いに独立しており,それぞれ平均6年および3年で指数分布に従う.よいドライバーからの最初の保険金支払い請求が3年以内に,悪いドライバーからの最初の保険金支払い請求が2年以内に発生する確率を求める:
天候 (3)
トラフィック (4)
信頼性 (5)
寿命が平均1000時間,標準偏差50時間でほぼ正規分布に従う電池がある.寿命が800時間から1000時間になる割合を求める:
100個の電池の中で寿命が800時間から1000時間であるものの数を計算する:
ある電化製品の寿命が平均10年で指数分布に従っているとする.この電化製品の寿命の分布を求める:
使用年数 ![]() 年の中古製品がさらに5年間故障しない確率を求める:
年の中古製品がさらに5年間故障しない確率を求める:
ExponentialDistributionの無記憶性を使う:
3つのマイクロプロセッサで三重の冗長度を使い,プロセッサが1つでも使用可能な場合に使えるように設計されているシステムがある.マイクロプロセッサが ![]() 秒後にも使用可能である確率は
秒後にも使用可能である確率は ![]() である.このシステムが
である.このシステムが ![]() 秒後にも稼働している確率を求める:
秒後にも稼働している確率を求める:
各プロセッサの故障までの平均時間が ![]() だとして,このシステムが確率99%未満で稼働している時間を求める:
だとして,このシステムが確率99%未満で稼働している時間を求める:
任意の試みで火の付く確率が0.90の安売りライターがある.着火プロセスのシミュレーションを行う.結果は着火に成功するまでの失敗回数を表す:
4つの独立部品で構成されているシステムがある.それぞれの部品の寿命は母数![]() の指数分布に従っている.500時間以内に故障する部品がひとつもない確率を求める:
の指数分布に従っている.500時間以内に故障する部品がひとつもない確率を求める:
SurvivalFunctionを直接使う:
最初の1200時間で厳密に1つの部品が故障する確率を求める:
CDFとSurvivalFunctionを直接使う:
BooleanCountingFunctionを使うことで論理条件も定義できる:
伝達 (4)
記号 n 個の文字列からなるパケットをノイズの多いチャンネルを使って送信する.それぞれの記号が不正確に送信される確率は![]() である.パケットが誤って送信される確率が
である.パケットが誤って送信される確率が![]() 未満になるような n を求める:
未満になるような n を求める:
電話の通話時間が指数分布に従うと仮定する.通話の平均時間は3.7分である.連続する9回の通話の合計が25分を超える確率を求める:
異なる4つの送信機からの信号を待つ受信機の待ち時間は母数がそれぞれ ![]() ,
,![]() ,
,![]() ,
,![]() の指数分布に従う.3番目の送信機からの信号が最初に受信機に届く確率を求める:
の指数分布に従う.3番目の送信機からの信号が最初に受信機に届く確率を求める:
![]() ,
,![]() ,
,![]() ,
,![]() について,受信機に届く信号間の待ち時間のシミュレーションを行う:
について,受信機に届く信号間の待ち時間のシミュレーションを行う:
論理素子における遅延時間は指数分布に従い,平均遅延は![]() 秒であると仮定する.組合せ論理網内の最長の論理素子のシーケンスは6個である.論理素子6個すべてを通過する際の遅延が
秒であると仮定する.組合せ論理網内の最長の論理素子のシーケンスは6個である.論理素子6個すべてを通過する際の遅延が![]() 秒より長くなる確率を求める:
秒より長くなる確率を求める:
品質 (4)
学生は合格するまで繰り返しテストを受ける.毎回の合格率は ![]() である.学生が
である.学生が ![]() 回以下の受験で合格する確率を求める:
回以下の受験で合格する確率を求める:
学生が ![]() 回以下の受験で合格するとして,その確率密度関数を求める:
回以下の受験で合格するとして,その確率密度関数を求める:
あるレストランでの客の待ち時間は平均5分間で指数分布に従うとする.客が10分を超えて待たなければならない確率を求める:
ある客がすでに10分待っているのにさらに10分待たなければならない確率を求める(過去は関係ない):
長さが平均0.497インチで標準偏差が0.002インチの正規分布に従う釘を生産している会社がある.長さが0.5インチプラスマイナス0.004インチという長さ指定を満足する釘の割合を求める:
CDFを使って直接計算する:
10個一束の製品のうち5個が不良品であり,そこから6個を検査のために取り出したとする.見付かった不良品の数を数える検査プロセスのシミュレーションを行う:
確率の可視化 (3)
その他の応用 (5)
放射性物質は1秒間に平均3.2個の ![]() 粒子を放出する.その分布を示す:
粒子を放出する.その分布を示す:
1秒間に放出される標準的な粒子数を10分間に渡ってシミュレーションする:
30%のケースで効果があると証明されている薬がある.この薬が4人のうち3人の患者に効く確率を求める:
ロジスティック分布は前日終値からの株価の変動率に非常によくフィットする.2000年1月1日から2009年1月1日までのスタンダード&プアーズ500種株価指数の日ごとの株価の変動率の推定分布を求める:
ロジスティック分布を使うとLogNormalDistributionを使った場合よりもよりよいフィットが得られることを示す:
男児か女児か (1)
三角形の構築 (1)
領域 (1)
DirichletDistributionについて,Disk上での確率を求める:
特性と関係 (11)
排反事象ではない事象については,共通集合の事象の確率を差し引く必要がある:
リストによって指定される分布については,Probabilityで相対頻度が計算できる:
分布の累積分布関数はProbabilityによって表すことができる:
分布の生存関数はProbabilityによって表すことができる:
分布のハザード関数はProbabilityによって表すことができる:
NProbabilityを使ってある事象の確率の数値を求める:
ある事象の確率はその事象のBooleのExpectationに等しい:
テキスト
Wolfram Research (2010), Probability, Wolfram言語関数, https://reference.wolfram.com/language/ref/Probability.html (2016年に更新).
CMS
Wolfram Language. 2010. "Probability." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/Probability.html.
APA
Wolfram Language. (2010). Probability. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Probability.html
BibTeX
@misc{reference.wolfram_2025_probability, author="Wolfram Research", title="{Probability}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/Probability.html}", note=[Accessed: 01-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_probability, organization={Wolfram Research}, title={Probability}, year={2016}, url={https://reference.wolfram.com/language/ref/Probability.html}, note=[Accessed: 01-March-2026]}