Probability
Probability[pred,xdist]
给出满足谓词 pred,且假设 x 服从概率分布 dist 的事件概率.
Probability[pred,xdata]
给出满足谓词 pred,且假设 x 服从由 data 给出的概率分布的事件概率.
Probability[pred,{x1,x2,…}dist]
给出满足 pred,且假设 {x1,x2,…} 服从多变量分布 dist 的事件概率.
Probability[pred,{x1dist1,x2dist2,…}]
给出满足 pred,且假设 x1、x2、… 是独立的并服从分布 dist1、dist2、… 的事件的概率.
Probability[pred1pred2,…]
给出满足 pred2 的 pred1 的条件概率.
更多信息和选项

- xdist 可以用 x
 dist
dist dist 或 x\[Distributed]dist 输入.
dist 或 x\[Distributed]dist 输入. - pred1pred2 可以用 pred1
 cond
cond pred2 或 pred1\[Conditioned]pred2 输入.
pred2 或 pred1\[Conditioned]pred2 输入. - 对于一个连续分布 dist,pred 的概率由 ∫Boole[pred]f[x]x 给出,其中 f[x] 是 dist 的概率密度函数,并且积分在 dist 的定义域上进行.
- 对于一个离散分布 dist,pred 的概率由 ∑Boole[pred]f[x] 给出,其中 f[x] 是 dist 的概率密度函数,并且加和在 dist 的定义域上进行.
- 对于数据集 data,pred 的概率由 Sum[Boole[pred],{x,data}]/Length[data] 给出.
- 一元数据以值 {v1,v2,…} 的列表形式给出,多元数据以向量 {{v11,…,v1m},{v21,…,v2m},…} 的列表形式给出.
- Probability[pred,{x1dist1,x2dist2}] 对应于 Expectation[Probability[pred,x2dist2],x1dist1],因此最后一个变量首先进行加和或积分.
- 如果无法得到符号式概率,N[Probability[…]] 将调用 NProbability. »
- 可以给定下列选项:
-
Assumptions $Assumptions 对参数所做的假设 » GenerateConditions False 是否生成关于参数的条件 Method Automatic 要使用何种方法 »
背景
- Probability[pred,x] 表示一个满足谓词 pred 的事件在选定随机变量 x 服从指定概率分布(即 是一个离散或连续的分布,如 NormalDistribution、BinomialDistribution、ChiSquareDistribution 等等)或取自给定数据集(即 定义了一个数据集)这一前提下的概率,其中 是 Distributed 的简写. Probability 的输出
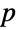 是一个满足
是一个满足 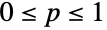 的数(其中不可能事件的概率是 0 而必然事件的概率是 1)或含有输入参数的符号表达式.
的数(其中不可能事件的概率是 0 而必然事件的概率是 1)或含有输入参数的符号表达式. - Probability 也适用于多变量分布;适用于非参数分布如 EmpiricalDistribution、HistogramDistribution 和 KernelMixtureDistribution;还适用于导出分布如 TransformedDistribution 和 ProductDistribution. 此外,Probability 可用于随机过程,包括由 ContinuousMarkovProcess、DiscreteMarkovProcess、WienerProcess 和 PoissonProcess 定义的那些.
- 谓词 pred 可以包含线性和非线性的不等式,以及不等式的逻辑组合. Probability 可以通过形如 pred1pred2 的谓词计算条件概率,其中 是 Conditioned 的简写. Probability 可以接受许多选项,包括 Assumptions、GenerateConditions 和 Method. Probability 提供的输出是用像符号积分与求和这样的精确方法计算的. 对应的使用数值方法的结果可以通过 NProbability 求得.
- 一些 Wolfram 语言中的函数,包括 PDF、CDF 及 SurvivalFunction,返回的结果等价于使用带有特定谓词结构的 Probability 求得的结果. 此外,用 Probability 求得的结果也可以用 Expectation 配合 Boole 结构求得 Expectation . 例如,Expectation[Boole[1<x<3],xNormalDistribution[]] 等价于 Probability[1<x<3,xNormalDistribution[]].
- Probability 可被用于精确求解许多概率论上的问题. 例如,投掷两个骰子和为 3 或 4 的概率可由 Probability[3≤x+y≤4,{x,y}DiscreteUniformDistribution[{{1,6},{1,6}}] 求得,而满足
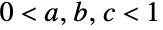 的均匀分布的随机变量三元组
的均匀分布的随机变量三元组 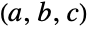 使多项式
使多项式 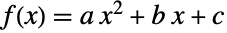 有实根的概率可用 Probability[b2-4a c≥0,{a,b,c}UniformDistribution[Table[{0,1},{3}]]] 计算.
有实根的概率可用 Probability[b2-4a c≥0,{a,b,c}UniformDistribution[Table[{0,1},{3}]]] 计算.
范例
打开所有单元关闭所有单元范围 (30)
基本用途 (9)
如果符号计算失败,则应用 N[Probability[…]] 来调用 NProbability:
在无 Assumptions的情况下生成条件:
如果有 Assumptions,则返回满足已知假设条件的有效结果:
Quantity 用法 (3)
非参数分布 (4)
使用一元 EmpiricalDistribution 计算概率:
使用一元 HistogramDistribution:
使用单元 KernelMixtureDistribution:
使用具有 SurvivalDistribution 的删截数据:
导出分布 (9)
使用 TransformedDistribution 计算概率:
使用 ProductDistribution 求概率:
选项 (5)
Assumptions (1)
无 Assumptions,生成条件:
有 Assumptions,返回在给定假设下的有效结果:
Method (4)
通过计算两个不同的 CDF,给出计算概率:
计算 TukeyLambdaDistribution 的事件概率:
以下使用 Quantile,因为分布的 PDF 没有解析解:
对于此例,可使用 Integrate:
用 Activate 来算出结果:
应用 (50)
随机实验 (8)
掷硬币实验包括重复抛掷一个均匀硬币 (fair coin) 直到获得正面向上的结果. 模拟该过程:
一枚均匀硬币抛掷 n 次,获得正面向上的次数可以用 BinomialDistribution 模拟:
计算抛掷硬币 100 次,得到正面的次数介于介于 60 和 80 间的概率:
用均匀硬币,获得 4 个正面 (head) 前得到反面 (tail) 的数量:
一个公正的六面骰子可以用 DiscreteUniformDistribution 来模拟:
体育和游戏 (4)
Gary Kasparov,国际象棋冠军,在锦标赛中同时对 100 个业余爱好者. 在这种比赛中估计他输的概率为 1%. 求他输 0、2、5 和10 场比赛的概率:
他打 5 场比赛时执行同样的计算,但是具有更强的对手,因此他输的概率为 10%:
在花旗骰 (Craps) 游戏中 [MathWorld],扔两个骰子:
求获得“两点”(snake eyes) 的概率[MathWorld]:
或“12 点”(boxcars)[MathWorld]:
或“8 点”(eighter from Decatur)[MathWorld]:
或“4 点”(little Joe)[MathWorld]:
精算学 (5)
精算师发现投保人三倍的可能索赔 2 次而不是 4 次. 如果索赔的次数为泊松分布,那么索赔的方差是多少?
团体保险包括小公司雇员的医疗报销. 一年报销的值 ![]() 为
为 ![]() ,其中
,其中 ![]() 是随机变量,当
是随机变量,当 ![]() 时,其密度函数与
时,其密度函数与 ![]() 成正比. 已知
成正比. 已知 ![]() 超过 10000,
超过 10000,![]() 超过 40000 的条件概率是多少?
超过 40000 的条件概率是多少?
两家保险公司对一家大公司进行保险投标. 该标必须在 2000 与 2200 之间. 如果两个标相差 20 以上,该公司决定接受低标的一家,否则,公司会进一步考虑两家投标保险公司. 假设两个标是独立的,在 2000 与 2200 区间内是均匀分布的. 决定该公司会进一步考虑两家投标保险公司的概率:
汽车保险索赔遵循正态分布,均值为 $194000,标准偏差为 $5000. 平均 25 个随机选择的索赔超过 $20000 的概率是多少?
优秀的司机的第一次索赔等待时间和蹩脚的司机第一次索赔等待时间是独立的且遵循指数分布,均值分别为 6 年和 3 年. 在 3 年内优秀司机的第一次索赔和在 2 年内蹩脚司机的第一次索赔的概率是多少?
气候 (3)
流通量 (4)
可靠度 (5)
电池寿命近似为正态分布,均值为 1000 小时,标准偏差为 50 小时. 求寿命在 800 与 1000 小时间的比例:
100 个电池中,计算有多少个寿命是在 800 到 1000 小时之间:
假设电器的寿命为指数分布且平均寿命为 10 年. 求电器的寿命分布:
使用 ExponentialDistribution 的无记忆属性:
一个系统采用具有 3 个微处理器的三重冗余,设计为只要一个微处理器仍然是工作的就可运作. ![]() 秒后一个微处理器仍然工作的概率为
秒后一个微处理器仍然工作的概率为 ![]() . 求一个系统
. 求一个系统 ![]() 秒后仍然运作的概率:
秒后仍然运作的概率:
每个处理器出故障的平均时间为 ![]() ,求出什么时候系统工作概率少于 99%:
,求出什么时候系统工作概率少于 99%:
一个预算价格的打火机打着的概率为 0.90. 模拟打火过程;结果显示成功点着前的失败次数:
一个系统由 4 个独立的组件构成,每个寿命服从指数分布,具有参数 ![]() . 求 500 小时前没有组件失效的概率:
. 求 500 小时前没有组件失效的概率:
直接使用 SurvivalFunction:
直接使用 CDF 和 SurvivalFunction:
使用 BooleanCountingFunction,你也可以定义逻辑条件:
通信 (4)
质量 (4)
学生会重复参加考试直至通过,每次成功的概率为 ![]() . 学生会重复参加考试直至通过,每次成功的概率为
. 学生会重复参加考试直至通过,每次成功的概率为 ![]() 次尝试时成功的概率:
次尝试时成功的概率:
假设学生在少于 ![]() 次尝试时通过考试,求概率密度函数 (PDF):
次尝试时通过考试,求概率密度函数 (PDF):
假设在饭店一位顾客的等候时间为指数分布,平均为 5 分钟. 求顾客等候超过 10 分钟的概率:
假设顾客已经等了至少 10 分钟(超过的没关系),求顾客还要等另外 10 分钟的概率:
一家公司制造钉子,长度为正态分布,均值为 0.497 英寸,标准偏差为 0.002 英寸. 求长度满足 0.5 英寸 ±0.004 英寸指标的比例:
用 CDF 直接计算:
概率可视化 (3)
其它应用 (5)
一种药物已被证明在 30% 的病例中有效. 求在 4 个病人中 3 个有效的概率:
对数分布对以前股票收盘价格的部分价格 (fractional price) 的变化提供很好的拟合. 求每天部分价格变化的估计分布,其中价格是 2000 年 1 月 1 号到 2009 年 1 月 1 号的标准普尔 500 指数:
使用对数分布比 LogNormalDistribution 提供更好的拟合:
三角形构建 (1)
区域 (1)
求 Disk 上 DirichletDistribution 的概率:
属性和关系 (11)
对于由列表指定的分布,Probability 计算的是相对频率:
分布的累积分布函数可以以 Probability 的形式表示:
一个分布的存活函数可以以 Probability 的形式表示:
分布的风险函数可以以 Probability 的形式表示:
用 NProbability 求一个事件的概率的数值:
一个事件的概率等价于该事件 Boole 的 Expectation:
文本
Wolfram Research (2010),Probability,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Probability.html (更新于 2016 年).
CMS
Wolfram 语言. 2010. "Probability." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/Probability.html.
APA
Wolfram 语言. (2010). Probability. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Probability.html 年