Quartiles

Quartiles[data]

list の要素の分位数推定を返す．

Quartiles[data,{{a,b},{c,d}}]

パラメータ a, b, c, d で指定された分位数の定義を使う．

Quartiles[dist]

分布 dist の分位数のリストを返す．

詳細

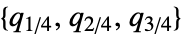  • は中央値と等価である． »
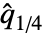  • は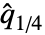， が奇数の場合は data のと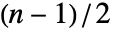の最小要素中央値の平均に等しく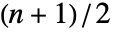， が偶数の場合は 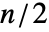の最小要素中央値に等しい．
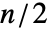  • は 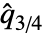のように定義されるが，最小要素ではなく最大要素によって定義される．
  • MatrixQ data については，四分位数は各列ベクトルについて計算される．Quartiles[{{x1,y1,…},{x2,y2,…},…}]は{Quartiles[{x1,x2,…}],Quartiles[{y1,y2,…}]}に等しい． »
  • ArrayQ data については，四分位数はArrayReduce[Quartiles,data,1]に等しい． »
  • Quartiles[data]はQuantile[data,{1,2,3}/4,{{1/2,0},{0,1}}]に等しい． »
  • Quartiles[data,{{a,b},{c,d}}]はQuantile[data,{1,2,3}/4,{{a,b},{c,d}}]に等しい．
  • 一般的に選ばれるパラメータ{{a,b},{c,d}}には以下がある．
  • {{0,0},{1,0}}経験的な累積分布関数の逆関数（デフォルト）
    {{0,0},{0,1}}線形補間（カリフォルニア法）
    {{1/2,0},{0,0}}p n に最も近い番号が付いた要素
    {{1/2,0},{0,1}}線形補間（水文学者法，デフォルト）
    {{0,1},{0,1}}平均ベースの推定（ワイブル法）
    {{1,-1},{0,1}}最頻値ベースの推定
    {{1/3,1/3},{0,1}}中央値ベースの推定
    {{3/8,1/4},{0,1}}正規分布の推定
  • 母数のデフォルトによる選択値は{{1/2,0},{0,1}}である． »
  • data は次の追加的な形式と解釈を持つことがある．
  • Association値（キーは無視される） »
    SparseArray配列として，Normal[data]に等しい »
    QuantityArray配列としての数量 »
    WeightedDataもとになっているEmpiricalDistributionに基づく »
    EventDataもとになっているSurvivalDistributionに基づく »
    TimeSeries, TemporalData, …ベクトルまたは値の配列（タイムスタンプは無視される） »
    Image,Image3DRGBチャンネル値またはグレースケール強度値 »
    Audioすべてのチャンネルの振幅値 »
    DateObject, TimeObject日付のリストまたは時間のリスト »
  • Quartiles[dist]は，Quantile[dist]に対応するリストを与える． »
  • ランダム過程 proc については，四分位関数は時点 t におけるスライス分布SliceDistribution[proc,t]についてQuartiles[SliceDistribution[proc,t]]として計算できる． »

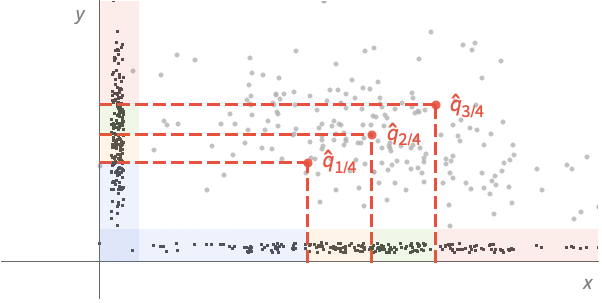
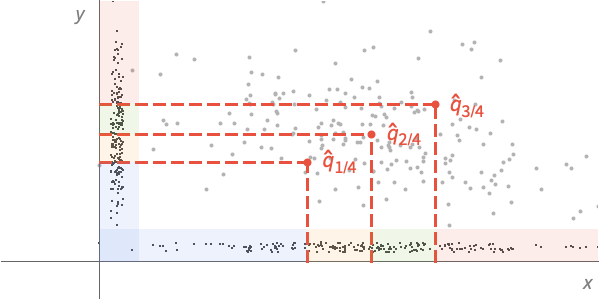
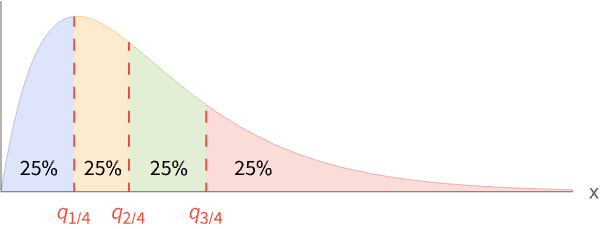
例題

すべて開くすべて閉じる

例  (3)

厳密数のリストの四分位数：

日付のリストの四分位数：

パラメトリック分布の四分位数：

スコープ  (22)

基本的な用法  (8)

厳密な入力は厳密な出力を与える：

近似入力は近似出力を与える：

他のパラメータ化を使って結果を計算する：

WeightedDataの四分位数を求める：

EventDataの四分位数を求める：

TemporalDataの四分位数を求める：

TimeSeriesの四分位数を求める：

四分位数は値のみに依存する：

数量を含むデータの四分位数を求める：

配列データ  (5)

行列についてのQuartilesは列ごと四分位数を与える：

テンソルについてのQuartilesは第1レベルの列ごとの中央値を与える：

大きい配列に使うことができる：

Quartilesは，入力がAssociationのときはその値に作用する：

SparseArrayデータは密な配列と同じように使うことができる：

QuantityArrayの四分位数を求める：

画像データと音声データ  (2)

RGB画像のチャンネルごとの四分位数値：

グレースケール画像の四分位強度値：

すべてのチャンネルの四分位振幅値：

日付と時間  (4)

日付の四分位数を計算する：

日付の重み付き四分位数を計算する：

異なる暦で与え荒れた日付の四分位数を計算する：

平均は入力の暦の一つで与えられる：

時間の四分位数を計算する：

異なる時刻帯指定の時刻のリスト：

分布と過程  (3)

パラメトリック分布の四分位数を求める：

派生分布の四分位数：

データ分布について：

ランダム過程についての四分位数関数：

アプリケーション  (4)

Quartilesは，分布を等確率の4区分に分割する：

時系列についての移動四分位数の包絡線を求める：

移動中央値で平滑化されたデータ：

第1，第3四分位数の移動エンベロープ：

2001年において産出量が最も多い油田を表すデータの四分位数を求める：

データの最大値および最小値を比較する：

四分位線を付けてデータをプロットする：

学級の生徒の身長の四分位数を計算する：

特性と関係  (6)

Quartilesは，線形に補間されたQuantileの値から得られる：

Quantileのデフォルトパラメータは異なる結果を与える：

データの第2四分位数はMedianである：

1/2の四分位数は，要素数が複数のリストについては2つの中間要素を平均しない：

InterquartileRangeは第1四分位数と第3四分位数の差分である：

QuartileDeviationは第1四分位数と第3四分位数の差分の半分である：

QuartileSkewnessは，四分位数から求められる歪度の測定値である：

BoxWhiskerChartはデータの四分位数を示す：

考えられる問題  (2)

Quartilesは data の数値を必要とする：

記号の閉じた形が存在する分布があるかもしれない：

Quantileによって計算されたデータの四分位が常にQuartilesと一致する訳ではない：

Quantileで線形補間パラメータを指定する：

Wolfram Research (2007), Quartiles, Wolfram言語関数， https://reference.wolfram.com/language/ref/Quartiles.html （2024年に更新）.

テキスト

Wolfram Research (2007), Quartiles, Wolfram言語関数， https://reference.wolfram.com/language/ref/Quartiles.html （2024年に更新）.

CMS

Wolfram Language. 2007. "Quartiles." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Quartiles.html.

APA

Wolfram Language. (2007). Quartiles. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Quartiles.html

BibTeX

@misc{reference.wolfram_2024_quartiles, author="Wolfram Research", title="{Quartiles}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Quartiles.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_quartiles, organization={Wolfram Research}, title={Quartiles}, year={2024}, url={https://reference.wolfram.com/language/ref/Quartiles.html}, note=[Accessed: 21-November-2024 ]}