RSolve

RSolve[eqn,a[n],n]

解递推方程，求 a[n].

RSolve[{eqn1,eqn2,…},{a1[n],a2[n],…},n]

求解递推方程组.

RSolve[eqn,a[n1,n2,…],{n1,n2,…}]

求解部分递推方程.

更多信息和选项

  • RSolve[eqn,a,n] 给出 a 为纯函数的解.
  • 方程可涉及形为 a[n+λ] 的对象，其中 λ 是常量，或推广为形式为 a[ψ[n]]、a[ψ[ψ[n]]、a[ψ[…[ψ[n]]…]] 的对象，ψ 可有以下形式：
  • n+λ算术差分方程
    μ n几何或 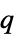差分方程
    μ n+λ算术-几何泛函差分方程
    μ nα几何-冪泛函差分方程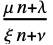
    线性分数泛函差分方程
  • 可用如 a[0]==val 这样的方程指定终止条件.
  • 如果没有指定足够的终止条件，RSolve 将给出通解，其中会引入未定常数.
  • 可通过指定 a∈Vectors[m] 或 a∈Matrices[{m,p}] 来表明自变量 a 的值是向量或矩阵. » »
  • 用连续的整数对由 RSolveValue 引入的常数进行索引. 选项 GeneratedParameters 指定应用于每个索引的函数. 默认为 GeneratedParameters->C ，它生成常数 C[1]、C[2] 等等.
  • GeneratedParameters->(Module[{C},C]&) 保证积分常数是唯一的，甚至在不同的 RSolve 调用之间.
  • 对于部分递推方程，RSolve 生成任意函数 C[n][…].
  • RSolve 给出的解在某些时候包括不能直接被 Sum 计算的和. 可在这样的和中使用有局部名称的虚变量.
  • RSolve 某些时候用 Solve 给出隐式解.
  • RSolve 可以处理常差分方程和 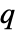差分方程.
  • RSolve 可处理差分-代数方程和常差分方程.
  • RSolve 可以求解常系数的任意阶线性递推方程. 它还可以求解许多非常数系数的最大阶数为二的线性方程，以及许多非线性方程.

范例

打开所有单元关闭所有单元

基本范例  (4)

求解一个差分方程：

包括边界条件：

求 a 的“纯函数”解：

将解代入表达式：

求解泛函方程：

范围  (40)

基本用途  (7)

计算一阶差分方程的通解：

通过加上初始条件获得特解：

绘制一阶差分方程的解：

制作数值表格：

通过在第二个参数中使用 a 验证差分方程的解：

获得高阶差分方程的通解：

特解：

求解差分方程组：

绘制解：

验证解：

求解部分差分方程：

获取特解：

绘制所得的解：

对通解中的任意常数使用不同名称：

线性差分方程  (7)

几何方程：

变系数的一阶方程：

一个三阶常系数方程：

初值条件：

绘制解：

二阶非齐次方程：

用初等函数表示的二阶变系数方程：

Euler–Cauchy（欧拉-柯西）方程：

通常，用特殊的函数表示解：

常系数高阶非齐次方程：

非线性微分分方程  (5)

可解的对数方程：

Riccati 方程：

用三角函数和双曲线函数表示的方程解：

高阶方程：

非线性卷积公式：

微分方程组  (8)

常系数线性系统：

边界条件：

绘制它们的解：

线性分式系统：

对角线系统：

带有多项式解的变系数线性系统：

线性常系数的微分代数方程组：

一个 index 为 2 的方程组：

用向量变量求解线性方程组：

用矩阵变量变量求解线性方程组：

求解常系数线性非齐次 ODE 方程组：

偏差分方程  (3)

一阶线性常系数偏差分方程：

将 Sin[2k] 函数代入自由函数 C[1]：

绘制所得的解：

2 阶、3 阶和 4 阶常系数线性方程组：

非齐次方程：

变系数线性方程：

Q 差分方程  (6)

一阶常系数的 差分方程：

相同的方程的等价表示：

初始值：

二阶方程：

三阶方程：

非齐次方程：

代入一个数值：

绘制解：

线性变系数方程：

非线性方程：

Riccati 方程：

一个线性常系数的 差分方程组：

泛函差分方程  (4)

求算术差分方程的通解：

验证解：

求解算术几何差分方程的初值问题：

绘制解的图线：

求解线性分数差分方程：

制作解的数值的表格：

求解几何幂差分方程：

验证解：

推广和延伸  (1)

无边界条件，给出了两个参数：

一个边界条件：

两个边界条件：

选项  (1)

GeneratedParameters  (1)

使用不同名称的常量：

使用有下标的常量：

应用  (11)

利率为 r，仅对本金 p 支付利息，对第 n 年的金额 a[n] 进行建模：

下面是金额为 a[n] 时支付的利息，也就是复合利率：

这里 a[n] 表示解决 n 个圆盘的河内塔 (Tower of Hanoi) 问题所需移动的次数：

这里 a[n] 表示用 2×1 个磁砖平铺 n×3 空间的方法的数量：

二进制搜索问题中要进行比较的次数：

快速傅立叶变换中算术运算的数量：

积分 满足微分方程：

积分 满足微分方程：

的极数系数的微分方程：

n×n 对角矩阵的行列式，其对角线 满足：

这个例子模拟 n 维单位球体的表面积 s[n]：

n 维单位球体的体积：

运用牛顿的方法计算 ， 或计算 ：

运用欧拉折线法计算 ：

求解描述Karatsuba的乘法运算的复杂度差分方程：

与教科书乘法的复杂性比较：

属性和关系  (9)

求满足微分方程和边界条件：

对应于 Sum 的微分方程：

对应于 Product 的微分方程：

RSolve 返回解的规则：

RSolveValue 返回解的表达式：

RSolve 求解差分方程的符号解：

RecurrenceTable 产生相同问题的过程解：

FindLinearRecurrence 求解列表的最小线性递归：

RSolve 求解满足递归的序列：

使用 RecurrenceFilter 进行信号滤波：

使用 RSolve 求解相应微分方程：

预测基于 ARProcess 的时间序列的下一个值：

用 RSolve 得到同样的结果：

用 RFixedPoints 求由两个递归方程组成的方程组的不动点：

用 RStabilityConditions 分析不动点的稳定性：

用不动点作为初始条件，求解方程组：

针对给定的初始条件求解方程组：

绘制解：

可能存在的问题  (5)

结果可能含有和符号和积符号：

大写的 和大写的 不能被用作自变量：

用小写的 或小写的 进行替换：

这个微分方程的解是唯一的一个序列：

一个函数唯一的等于周期为 1 的函数：

边界值问题可能有多个解：

验证方程涉及到有下标的变量时的解：

巧妙范例  (1)

一个函数重复或组合 n 次的计算：

Wolfram Research (2003)，RSolve，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RSolve.html （更新于 2023 年）.

文本

Wolfram Research (2003)，RSolve，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RSolve.html （更新于 2023 年）.

CMS

Wolfram 语言. 2003. "RSolve." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2023. https://reference.wolfram.com/language/ref/RSolve.html.

APA

Wolfram 语言. (2003). RSolve. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RSolve.html 年

BibTeX

@misc{reference.wolfram_2024_rsolve, author="Wolfram Research", title="{RSolve}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/RSolve.html}", note=[Accessed: 13-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rsolve, organization={Wolfram Research}, title={RSolve}, year={2023}, url={https://reference.wolfram.com/language/ref/RSolve.html}, note=[Accessed: 13-November-2024 ]}