RadonTransform

expr のラドン変換を与える．

詳細とオプション

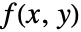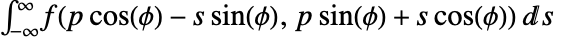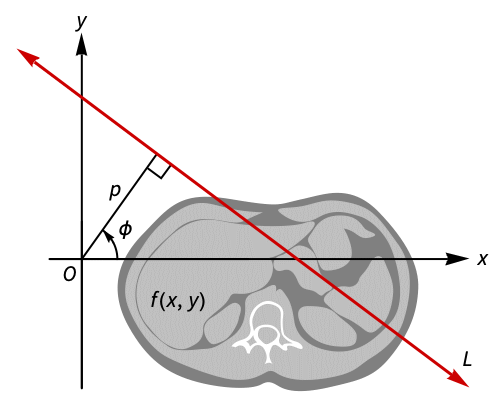
関数のラドン変換は，と定義される．
幾何学的には，ラドン変換は，方程式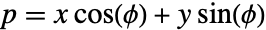（-∞<p<∞，-π/2<ϕ<π/2）によって標準形で与えらる直線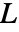に沿った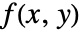の積分を表す．

次は使用可能なオプションである．

Assumptions	$Assumptions	パラメータについての仮定
GenerateConditions	False	パラメータについての条件を含む結果を生成するかどうか
Method	Automatic	使用するメソッド

TraditionalFormでは，RadonTransformはを使って出力される．

例題

すべて開くすべて閉じる

例 (1)

関数のラドン変換を計算する：

関数を変換と一緒にプロットする：

スコープ (10)

基本的な用法 (2)

記号パラメータ値について，関数のラドン変換を計算する：

パラメータに厳密値を使う：

パラメータに非厳密値を使う：

ラドン変換の有効性の条件を得る：

仮定を指定する：

ガウス関数 (5)

円形ガウス関数のラドン変換：

関数を変数と一緒にプロットする：

楕円ガウス関数のラドン変換：

関数を変数と一緒にプロットする：

多項式とガウス関数の積：

エルミート多項式とガウス関数の積：

三角関数とガウス関数の積：

区分関数と一般化された関数 (3)

単位円板についての特性関数のラドン変換：

多項式と，単位円板についての特性関数の積：

DiracDeltaを含む式のラドン変換：

オプション (2)

Assumptions (1)

仮定を指定する：

GenerateConditions (1)

結果の有効性についての条件を生成する：

アプリケーション (2)

円板の特性関数についての記号ラドン変換を計算する：

Radonを使って同じ結果を得る：

ラドン変換を使ってポアソン(Poisson)方程式を解く：

RadonTransformを方程式に適用する：

DSolveValueを使って常微分方程式を解く：

解における任意定数を0に設定する：

InverseRadonTransformを使ってもとの方程式の解を得る：

解を確かめる：

解をプロットする：

特性と関係 (10)

RadonTransformは積分を計算する：

Integrateを使って同じ結果を得る：

RadonTransformとInverseRadonTransformは互いに逆の関係にある：

RadonTransformは線形演算子である：

RadonTransformのシフト特性：

RadonTransformの対称特性：

のラドン変換を，単位ベクトルによって表す：

対称特性を確かめる：

RadonTransformの同質性特性：

のラドン変換を，単位ベクトルによって表す：

同質性特性を確かめる：

RadonTransformのスケーリング特性：

のラドン変換を，単位ベクトルによって表す：

スケーリング特性を確かめる：

導関数のRadonTransform：

LaplacianのRadonTransform：

RadonTransformは，フーリエ変換を使って計算できる：

f のフーリエ変換を極座標で計算する：

逆フーリエ変換を計算してラドン変換を得る：

RadonTransformを直接使って同じ結果を得る：

おもしろい例題 (1)

基本的なラドン変換の表を作る：

Top

その他のラーニングリソース

テクニカルサポート

Wolframソリューション

教育のためのWolframソリューション

使い始める

Grow Your Skills

Wolframと繋がる

大人用の教育プログラム

若者のための教育プログラム

読む

RadonTransform

詳細とオプション

例題

例 (1)