Rotate
Rotate[g,θ]
represents 2D graphics primitives or any other objects g rotated counterclockwise by θ radians about the center of their bounding box.
Rotate[g,θ,{x,y}]
rotates about the point {x,y}.
Rotate[g,{u,v}]
rotates around the origin, transforming the 2D or 3D vector u to v.
Rotate[g,θ,w]
rotates 3D graphics primitives by θ radians around the 3D vector w anchored at the origin.
Rotate[g,θ,w,p]
rotates around the 3D vector w anchored at p.
Rotate[g,θ,{u,v}]
rotates by angle θ in the plane spanned by 3D vectors u and v.
Details and Options

- θ Degree or θ° specifies an angle in degrees.
- If Rotate appears outside a graphic, the object g in Rotate[g,θ] etc. can be any expression.
- You can specify special points such as {Left,Bottom} within the bounding box for g.
- The x position can be specified as Left, Center, or Right; the y position as Bottom, Center, or Top.
- If Rotate appears within a graphic, the coordinates {x,y} are taken to be in the coordinate system of the graphic.
- If Rotate appears outside a graphic, the coordinates {x,y} are taken to run from
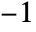 to
to 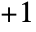 across the bounding box of the object being rotated.
across the bounding box of the object being rotated. - Rotate[g,θ] is equivalent to Rotate[g,θ,{Center,Center}].
- For objects specified with scaled coordinates Scaled[{x,y}], Rotate effectively applies its transformation to the corresponding ordinary coordinates.
- If Rotate appears inside a graphic, Normal[expr] if possible replaces all Rotate[gi,…] constructs by versions of the gi in which the coordinates have explicitly been transformed.
Examples
open allclose allBasic Examples (3)
Scope (8)
Properties & Relations (1)
When possible, Normal will transform the coordinates explicitly:
Possible Issues (4)
By default, Rotate uses the center of the bounding box as the center of rotation:
Explicitly specify a center of rotation:
Transforming an object may move it out of view:
Adjust the PlotRange to display the transformed object:
The center of the baseline of rotated text aligns with the baseline of the surrounding text:
For a different alignment, specify an explicit center of rotation:
Since text bounding boxes are always rectilinear, successive rotations can introduce extra space:
Text
Wolfram Research (2007), Rotate, Wolfram Language function, https://reference.wolfram.com/language/ref/Rotate.html (updated 2008).
CMS
Wolfram Language. 2007. "Rotate." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/Rotate.html.
APA
Wolfram Language. (2007). Rotate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Rotate.html