RotationMatrix
gives the 2D rotation matrix that rotates 2D vectors counterclockwise by θ radians.
RotationMatrix[θ,w]
gives the 3D rotation matrix for a counterclockwise rotation around the 3D vector w.
RotationMatrix[{u,v}]
gives the matrix that rotates the vector u to the direction of the vector v in any dimension.
RotationMatrix[θ,{u,v}]
gives the matrix that rotates by θ radians in the plane spanned by u and v.
Details and Options

- RotationMatrix gives matrices for rotations of vectors around the origin.
- Two different conventions for rotation matrices are in common use.
- RotationMatrix is set up to use the vector-oriented convention and to give a matrix m so that m.r yields the rotated version of a vector r.
- Transpose[RotationMatrix[…]] gives rotation matrices with the alternative coordinate-system-oriented convention for which r.m yields the rotated version of a vector r.
- Angles in RotationMatrix are in radians. θ Degree or θ° specifies an angle in degrees.
- Positive θ in RotationMatrix[θ,{u,v}] corresponds to going from the direction of u towards the direction of v.
- RotationMatrix[θ] is equivalent to RotationMatrix[θ,{{1,0},{0,1}}].
- RotationMatrix[θ,w] is equivalent to RotationMatrix[θ,{u,v}], where u⊥w, v⊥w, and u,v,w form a right-handed coordinate system.
- RotationMatrix gives an orthogonal matrix of determinant 1, that in
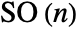 dimensions can be considered an element of the group
dimensions can be considered an element of the group 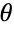 .
. - RotationMatrix supports the option TargetStructure, which specifies the structure of the returned matrix. Possible settings for TargetStructure include:
-
Automatic automatically choose the representation returned "Dense" represent the matrix as a dense matrix "Orthogonal" represent the matrix as an orthogonal matrix "Unitary" represent the matrix as a unitary matrix - RotationMatrix[…,TargetStructureAutomatic] is equivalent to RotationMatrix[…,TargetStructure"Dense"].
Examples
open allclose allBasic Examples (4)
Scope (6)
A 4D rotation matrix, rotating in the ![]() plane:
plane:
A general 3D rotation matrix, rotating in the plane given by t{1,1,1} + s{1,–2,1}:
Rotate the vector {1,0,0} to the vector {0,0,1}:
Generate the rotation matrix for symbolic vectors, assuming that all quantities are real:
Rotating {0,0,1} gives the normalized {x,y,z} vector:
Options (1)
Applications (2)
Properties & Relations (9)
A rotation matrix is orthogonal, i.e. the inverse is equal to the transpose:
In the complex case, the rotation matrix is unitary:
A rotation matrix has determinant ![]() :
:
Multiplying by the rotation matrix preserves the norm of a vector:
The inverse of RotationMatrix[θ,{u,v}] is given by RotationMatrix[-θ,{u,v}]:
The inverse of RotationMatrix[θ,{u,v}] is also given by RotationMatrix[θ,{v,u}]:
If u or v is not real the relationship is more complex:
In 2D the inverse of RotationMatrix[θ] is given by RotationMatrix[-θ]:
In 3D the inverse of RotationMatrix[θ,w] is given by RotationMatrix[θ,-w]:
Possible Issues (1)
Text
Wolfram Research (2007), RotationMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/RotationMatrix.html (updated 2024).
CMS
Wolfram Language. 2007. "RotationMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/RotationMatrix.html.
APA
Wolfram Language. (2007). RotationMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RotationMatrix.html