RotationMatrix

RotationMatrix[θ]

2Dベクトルを反時計回りに θ ラジアン分回転した2D回転行列を返す．

RotationMatrix[θ,w]

3Dベクトル w の周囲を反時計回りに回転した3D回転行列を返す．

RotationMatrix[{u,v}]

任意の次元でベクトルu をベクトル v の方向に回転した行列を返す．

RotationMatrix[θ,{u,v}]

u と v でスパンした平面上で θ ラジアン回転した行列を返す．

詳細とオプション

  • RotationMatrixは原点周囲でベクトルを回転した行列を与える．
  • 回転行列では2種類の異なる慣習が一般的に使われている．
  • RotationMatrixはベクトルに基づいて表した場合，m.r がベクトル r を回転したものを与えるような行列 m を与えるように設定されている．
  • Transpose[RotationMatrix[…]]は，r.m がベクトル r を回転したものを返す，別の座標系指向の慣習を使う回転行列を返す．
  • RotationMatrixにおける角はラジアンで与えられる．θ Degreeすなわち θ°は角を度で指定する．
  • RotationMatrix[θ,{u,v}]における正の θ は，u 方向から v 方向への移動に相当する．
  • RotationMatrix[θ]はRotationMatrix[θ,{{1,0},{0,1}}]に等しい．
  • RotationMatrix[θ,w]はu⊥w と v⊥w と u,v,w で右手座標形を形成する場合，RotationMatrix[θ,{u,v}]に等しい
  • RotationMatrixは，行列式が1の対角行列を返し， 次元の場合，グループ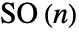の一つであると考えられる，行列式が1の対角行列を返す．
  • RotationMatrixは，返す行列の構造を指定するオプションTargetStructureをサポートする．次は， TargetStructureの可能な設定である．
  • Automatic返す表現を自動選択する
    "Dense"行列を密な行列として表す
    "Orthogonal"行列を直交行列として表す
    "Unitary"行列をユニタリ行列として表す
  • RotationMatrix[…,TargetStructureAutomatic]はRotationMatrix[…,TargetStructure"Dense"]に等しい．

例題

すべて開くすべて閉じる

例  (4)

原点付近でベクトルを回転させる一般的な2D回転行列：

単位ベクトルに 方向への の回転を適用する：

反時計回りに30°回転させる：

{1,1}という方向を{0,–1}という方向に変化させる回転：

軸周辺の3D回転：

スコープ  (6)

平面で回転している4D回転行列：

t{1,1,1} + s{1,–2,1}で与えられる平面上で回転している一般的な3D回転行列：

ベクトル{1,0,0}を回転させてベクトル{0,0,1}にする：

すべての数量が正であると仮定して，記号ベクトルの回転行列を生成する：

{0,0,1}を回転すると正規化された{x,y,z}ベクトルが与えられる：

2Dの形に適用された変換：

3Dの形に適用された変換：

オプション  (1)

TargetStructure  (1)

回転行列を密な行列として返す：

回転行列を直交行列として返す：

回転行列をユニタリ行列として返す：

アプリケーション  (2)

3Dの形を回転させる：

次元のすべての回転の基礎を作る：

2Dのすべての回転：

3Dのすべての回転：

4Dのすべての回転．一般に 次元には の基礎要素が必要である：

特性と関係  (9)

回転行列は直交する，すなわち，逆行列は転置に等しい：

複素数の場合，回転行列はユニタリ行列である：

回転行列は行列式を持つ：

回転行列倍するとベクトルのノルムが保存される：

RotationMatrix[θ,{u,v}]の逆行列はRotationMatrix[-θ,{u,v}]で与えられる：

RotationMatrix[θ,{u,v}]の逆行列は，RotationMatrix[θ,{v,u}]によっても与えられる：

u あるいは v が実数ではない場合，この関係はより複雑になる：

2Dでは，RotationMatrix[θ]の逆行列はRotationMatrix[-θ]で与えられる：

3Dでは，RotationMatrix[θ,w]の逆行列はRotationMatrix[θ,-w]で与えられる：

w が実数ではない場合，この関係はより複雑になる：

回転中の回転の構成：

考えられる問題  (1)

回転を行う順番が重要である：

の周りで回転させ，次に の周りで回転させるのは，まず の周りで回転させ，次に の周りで回転させるのとは異なる：

おもしろい例題  (1)

扇形の回転：

Wolfram Research (2007), RotationMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/RotationMatrix.html （2024年に更新）.

テキスト

Wolfram Research (2007), RotationMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/RotationMatrix.html （2024年に更新）.

CMS

Wolfram Language. 2007. "RotationMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/RotationMatrix.html.

APA

Wolfram Language. (2007). RotationMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RotationMatrix.html

BibTeX

@misc{reference.wolfram_2024_rotationmatrix, author="Wolfram Research", title="{RotationMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RotationMatrix.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rotationmatrix, organization={Wolfram Research}, title={RotationMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/RotationMatrix.html}, note=[Accessed: 21-November-2024 ]}