SemidefiniteOptimization
SemidefiniteOptimization[f,cons,vars]
半定値制約 cons に従って線形目的関数 f を最小化する変数 vars の値を求める.
SemidefiniteOptimization[c,{a0,a1,…,ak}]
線形行列不等式制約 ![]() に従って数量
に従って数量 ![]() を最小化するベクトル
を最小化するベクトル ![]() を求める.
を求める.
SemidefiniteOptimization[…,"prop"]
解のどの特性"prop"を返すべきかを指定する.
詳細とオプション




- SemidefiniteOptimizationは,半定値計画法(SDP)および混合整数半定値計画法(MISDP)としても知られている.
- 半定値最適化は,実変数,整数変数あるいは複素変数で大域的かつ効率的に解ける凸最適化問題である.
- 半定値最適化は,主問題を解く
 を求める.
を求める. -
最小化 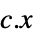
制約条件 ![a_(0)+a_(1) x_(1)+...+a_(k) x_(k)>=_(TemplateBox[{n}, SemidefiniteConeList])0 a_(0)+a_(1) x_(1)+...+a_(k) x_(k)>=_(TemplateBox[{n}, SemidefiniteConeList])0](Files/SemidefiniteOptimization.ja/6.png)
ただし, 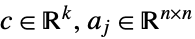
- 行列
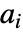 は対称
は対称 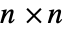 行列でなければならない.
行列でなければならない. - 混合整数の半定値最適化は,問題を解く
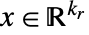 および
および 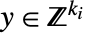 を求める.
を求める. -
最小化 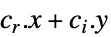
制約条件 ![a_(0)+a_(1) x_(1)+...+a_(k_r) x_(k_r)+a_(k_r+1)y_1+...+a_(k_r+k_i)y_(k_i)>=_(TemplateBox[{n}, SemidefiniteConeList])0 a_(0)+a_(1) x_(1)+...+a_(k_r) x_(k_r)+a_(k_r+1)y_1+...+a_(k_r+k_i)y_(k_i)>=_(TemplateBox[{n}, SemidefiniteConeList])0](Files/SemidefiniteOptimization.ja/13.png)
ただし, 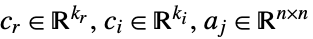
- SemidefiniteOptimizationは,目的関数が実数値のときは,内部的に実変数
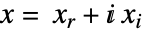 に変換して
に変換して ![x in TemplateBox[{}, Complexes]^n x in TemplateBox[{}, Complexes]^n](Files/SemidefiniteOptimization.ja/16.png) の問題を解く.ただし,
の問題を解く.ただし, で
で 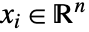 である.線形行列不等式はエルミート行列
である.線形行列不等式はエルミート行列  で指定できるかもしれない.
で指定できるかもしれない. - 変数指定 vars は,次のいずれかの形式で変数を与える要素のリストでなければならない.
-
v 名前が  で次元が推測される変数
で次元が推測される変数v∈Reals 実数のスカラー変数 v∈Integers 整数のスカラー変数 v∈Complexes 複素数のスカラー変数 v∈ℛ 幾何学次元 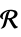 に制限されたベクトル変数
に制限されたベクトル変数v∈Vectors[n,dom] 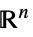 または
または のベクトル変数
のベクトル変数v∈Matrices[{m,n},dom] 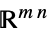 または
または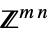 の行列変数
の行列変数 - 制約条件 cons は以下で指定できる.
-
LessEqual 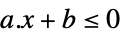
スカラー不等式 GreaterEqual 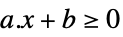
スカラー不等式 VectorLessEqual 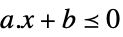
ベクトル不等式 VectorGreaterEqual 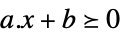
ベクトル不等式 Equal 
スカラー等式またはベクトル等式 Element 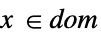
凸領域あるいは領域要素 - SemidefiniteOptimization[f,cons,vars]のとき parval の形のパラメータ方程式(par は vars に含まれず,val は数値あるいは数値配列)は制約条件に含まれて f あるいは cons で使われるパラメータを定義することがある. »
- 主最小化問題は,関連する最大化問題(ラグランジュの双対問題)を有する.双対最大値は,常に主最小値以下であるので,下限を与える.双対マキシマイザは,制約条件における変化に対する最小値の感度を含む主問題についての情報を与える. »
- 半定値最適化は次の双対を持つ. »
-
最大化 ![-TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {2ColumnTableMod}][a_0.lambda] -TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {2ColumnTableMod}][a_0.lambda]](Files/SemidefiniteOptimization.ja/33.png)
制約条件 ![TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {2ColumnTableMod}][a_j.lambda]=c_j,j=1,..., k,lambda>=_(TemplateBox[{n}, SemidefiniteConeList])0 TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {2ColumnTableMod}][a_j.lambda]=c_j,j=1,..., k,lambda>=_(TemplateBox[{n}, SemidefiniteConeList])0](Files/SemidefiniteOptimization.ja/34.png)
ただし 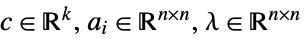
- 次は,可能な解の特性"prop" である.
-
"PrimalMinimizer" 
目的関数を最小化する変数値のリスト "PrimalMinimizerRules" 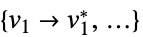
 を最小化する変数の値 vars={v1,…}
を最小化する変数の値 vars={v1,…} "PrimalMinimizerVector" 
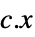 を最小化するベクトル
を最小化するベクトル"PrimalMinimumValue" 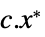
主最小値 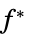
"DualMaximizer" 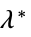
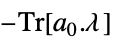 を最大化するベクトル
を最大化するベクトル "DualMaximumValue" ![-TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {3ColumnTableMod}][a_0.lambda^*] -TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {3ColumnTableMod}][a_0.lambda^*]](Files/SemidefiniteOptimization.ja/45.png)
双対最大値 "DualityGap" ![-TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {3ColumnTableMod}][a_0.lambda^*] - c.x^* -TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {3ColumnTableMod}][a_0.lambda^*] - c.x^*](Files/SemidefiniteOptimization.ja/46.png)
双対最適値と主最適値の差 "Slack" 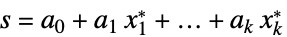
不等式制約を等式制約に変換する行列 "ConstraintSensitivity" 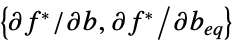
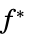 の制約摂動に対する感度
の制約摂動に対する感度"ObjectiveVector" 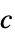
線形目的ベクトル "ConstraintMatrices" 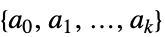
制約行列のリスト {"prop1","prop2",…} いくつかの解の特性 - 次は,使用可能なオプションである.
-
MaxIterations Automatic 使用する最大反復回数 Method Automatic 使用するメソッド PerformanceGoal $PerformanceGoal 最適化するパフォーマンスの局面 Tolerance Automatic 内部比較に使用する許容度 - オプションMethod->method を使って使用するメソッドを指定することができる.以下は,使用可能なメソッドである.
-
Automatic メソッドを自動的に選択する "CSDP" CSDP(COIN半定値計画)ライブラリ "DSDP" DSDP(半定値計画)ライブラリ "SCS" SDP(錐ソルバの分割)ライブラリ "MOSEK" 商用MOSEK凸最適化ソルバ - 計算はMachinePrecisionに限定される.
例題
すべて開くすべて閉じる例 (3)
スコープ (29)
基本的な用法 (13)
ベクトル変数 ![]() とInactive[Plus]を使って意図しないスレッディングを回避する:
とInactive[Plus]を使って意図しないスレッディングを回避する:
ベクトル変数 ![]() とパラメータ方程式を使って意図しないスレッディングを回避する:
とパラメータ方程式を使って意図しないスレッディングを回避する:
ベクトル変数 ![]() とIndexed[x,i]を使って個々の成分を指定する:
とIndexed[x,i]を使って個々の成分を指定する:
Vectors[n]を使って,曖昧な場合にベクトル変数の次元を指定する:
VectorGreaterEqualで複数の線形不等式制約表すことができる:
![]() v>=
v>=![]() あるいは\[VectorGreaterEqual]を使ってベクトル不等式の記号を入力する:
あるいは\[VectorGreaterEqual]を使ってベクトル不等式の記号を入力する:
NonNegativeReals (![]() )を使って非負の制約条件を指定する:
)を使って非負の制約条件を指定する:
整数変数 (4)
Integersを使って整数領域制約を指定する:
Vectors[n,Integers]を使ってベクトル変数に整数領域制約を指定する:
NonNegativeIntegers (![]() )を使って非負の整数領域制約を指定する:
)を使って非負の整数領域制約を指定する:
NonPositiveIntegers (![]() )を使って非正の整数領域制約を指定する:
)を使って非正の整数領域制約を指定する:
複素変数 (2)
Complexesを使って複素変数を指定する:
主モデルの特性 (3)
双対モデルの特性 (3)
オプション (8)
Method (5)
メソッドによってデフォルトの許容度は異なる.このことは精度と確度に影響する:
デフォルトメソッドの"CSDP"がメッセージを出す場合は,まず"DSDP"を試すとよい:
"SCS"を使った結果の質は,Toleranceを小さくすると向上することが多い:
PerformanceGoal (1)
オプションPerformanceGoalのデフォルト値は$PerformanceGoalである:
PerformanceGoal"Quality"を使ってより正確な結果を得る:
PerformanceGoal"Speed"を使って,質は犠牲にしてもより速く解を得る:
アプリケーション (33)
基本的なモデリング変換 (13)
![]() に従って
に従って ![]() を最大化する.目的関数を否定することで最大化問題を解く:
を最大化する.目的関数を否定することで最大化問題を解く:
決定変数![]() に線形依存する対称行列
に線形依存する対称行列 ![]() の最大固有値を最小化する
の最大固有値を最小化する![]() を求める.
を求める.![]() は
は ![]() に等しいので,この問題は線形行列不等式として立式できる.ただし,
に等しいので,この問題は線形行列不等式として立式できる.ただし,![]() は
は ![]() の
の ![]() 番目の固有値である.線形行列関数
番目の固有値である.線形行列関数 ![]() を定義する:
を定義する:
実対称行列 ![]() は直交行列
は直交行列 ![]() で対角化できる.したがって,
で対角化できる.したがって,![]() .ゆえに,
.ゆえに,![]() のときかつそのときに限り
のときかつそのときに限り ![]() .任意の
.任意の ![]() について
について ![]() を取ると,
を取ると,![]() .したがって,
.したがって,![]() のときかつそのときに限り
のときかつそのときに限り ![]() .数値的にシミュレーションを行って,これらの式が等しいことを示す:
.数値的にシミュレーションを行って,これらの式が等しいことを示す:
モンテカルロシミュレーションを行なって結果の妥当性をチェックする:
決定変数![]() に線形依存する対称行列
に線形依存する対称行列![]() の最小固有値を最大化する
の最小固有値を最大化する![]() を求める.線形行列関数
を求める.線形行列関数 ![]() を定義する:
を定義する:
![]() は
は ![]() に等しいので(ただし,
に等しいので(ただし,![]() は
は ![]() の
の ![]() 番目の固有値),この問題は線形行列不等式として立式できる.
番目の固有値),この問題は線形行列不等式として立式できる.![]() を最大化するために
を最大化するために![]() を最小化する:
を最小化する:
モンテカルロシミュレーションを実行して結果の妥当性をチェックする:
決定変数![]() に線形依存する対称行列
に線形依存する対称行列 ![]() の最大固有値と最小固有値の差を最小にする
の最大固有値と最小固有値の差を最小にする![]() を求める.線形行列関数
を求める.線形行列関数 ![]() を定義する:
を定義する:
![]() は
は ![]() と等しいので(ただし,
と等しいので(ただし,![]() は
は ![]() の
の ![]() 番目の固有値),この問題は,線形行列不等式として立式できる.結果の問題を解く:
番目の固有値),この問題は,線形行列不等式として立式できる.結果の問題を解く:
![]() において線形の対称行列
において線形の対称行列 ![]() の絶対値が最大の固有値を最小化する:
の絶対値が最大の固有値を最小化する:
最大固有値は ![]() を満足する.絶対値が最大の
を満足する.絶対値が最大の ![]() の負の固有値は
の負の固有値は![]() の最大固有値で,
の最大固有値で,![]() を満足する:
を満足する:
![]() の最大特異値
の最大特異値 ![]() は
は ![]() の最大固有値の平方根で,上記の例から
の最大固有値の平方根で,上記の例から ![]() か
か ![]() を満足する:
を満足する:
![]() を最小化する.補助変数
を最小化する.補助変数 ![]() を使うと,問題は
を使うと,問題は![]() となるように
となるように ![]() を最小化するものに変化する.これは
を最小化するものに変化する.これは![]() に等しい:
に等しい:
シューアの補題の制約条件には,![]() であれば,
であれば,![]() のときかつそのときに限りブロック行列
のときかつそのときに限りブロック行列![]() とある.したがって,
とある.したがって,![]() は0でなければならないから,
は0でなければならないから,![]() および
および ![]() について,
について,![]() ⧦
⧦ ![]() :
:
![]() に従い,
に従い,![]() のときは
のときは ![]() であると仮定して,
であると仮定して,![]() を最小化する.補助変数
を最小化する.補助変数 ![]() を使うと,目的は
を使うと,目的は![]() となるように
となるように ![]() を最小化することになる:
を最小化することになる:
シューアの補題の制約条件を使うと,![]() のときかつそのときに限り
のときかつそのときに限り![]() である.スレッディングを回避するための制約条件の構築にInactive[Plus]を使う:
である.スレッディングを回避するための制約条件の構築にInactive[Plus]を使う:
楕円体,二次の円錐と放物体を含む二次集合 ![]() について,
について,![]() かどうかを判定する.ただし,
かどうかを判定する.ただし,![]() は対称行列,
は対称行列,![]() はベクトル,
はベクトル,![]() はスカラーである:
はスカラーである:
集合 ![]() が全次元であると仮定すると,S-procedureは,
が全次元であると仮定すると,S-procedureは,![]() となるような非負の数
となるような非負の数 ![]() が存在するときかつそのときに限り
が存在するときかつそのときに限り ![]() であるとする.そのような非負の
であるとする.そのような非負の ![]() が存在することを,視覚的に確認する:
が存在することを,視覚的に確認する:
![]() に従って
に従って![]() を最小化する.目的関数
を最小化する.目的関数![]() を,追加の
を,追加の![]() に等しい制約条件
に等しい制約条件![]() を加えて線形関数
を加えて線形関数 ![]() に変換する:
に変換する:
![]() に従って
に従って![]() を最小化する.目的関数を
を最小化する.目的関数を![]() を使って線形関数と追加的な制約条件
を使って線形関数と追加的な制約条件![]() に変換する:
に変換する:
![]() に従って
に従って![]() を最小化する.目的関数を追加的な,
を最小化する.目的関数を追加的な,![]() と等しい制約条件
と等しい制約条件![]() がある線形関数
がある線形関数 ![]() に変換する:
に変換する:
![]() に従って
に従って ![]() を最小化する.ただし,
を最小化する.ただし,![]() は非減少関数で
は非減少関数で ![]() を最小化する.主ミニマイザ
を最小化する.主ミニマイザ ![]() は両方の問題で同じである.
は両方の問題で同じである.![]() に従って
に従って ![]() を最小化することを考える:
を最小化することを考える:
データフィッティング問題 (5)
離散データ集合をフィットする![]() を最小化することで五次多項式の係数
を最小化することで五次多項式の係数 ![]() を求める:
を求める:
多項式の基底を選択し,DesignMatrixと出力ベクトルを使って入力行列を構築する:
補助変数 ![]() を使うと,目的は
を使うと,目的は![]() となるように
となるように ![]() を最小化することに変換される.これは,基本的なモデリング変換でも示したように,
を最小化することに変換される.これは,基本的なモデリング変換でも示したように,![]() に等しい:
に等しい:
チェビシェフ(Chebyshev)基底を使って![]() を最小化することで,対数スケールで変化する離散データの近似関数を求める:
を最小化することで,対数スケールで変化する離散データの近似関数を求める:
チェビシェフ基底関数を選択してランダムなデータ点におけるその値を計算する:
データは対数スケールなので,直接データをフィットすることは望ましくない.代りに,問題を変換して![]() を最小化することにする.補助変数
を最小化することにする.補助変数 ![]() を使って
を使って![]() となるように
となるように ![]() を最小化する.この制約条件は
を最小化する.この制約条件は に等しい:
に等しい:
データのフィットは関数Fitを使って直接求めることもできる.しかし,対数変換なしでは,近似関数にかなりの摂動が見られる:
目的は,![]() となるような
となるような ![]() を求めることである.ただし,
を求めることである.ただし,![]() は単項式のベクトルである:
は単項式のベクトルである:
二次の項 ![]() .ただし,
.ただし,![]() は
は ![]() のコレスキー(Cholesky)分解で得られた下三角行列である:
のコレスキー(Cholesky)分解で得られた下三角行列である:
濃度で制約された最小二乗問題.![]() が最大で
が最大で ![]() 個の非零要素を持つように
個の非零要素を持つように![]() を最小化する:
を最小化する:
![]() が,もし
が,もし ![]() ならば
ならば ![]() は非零となるような決定ベクトルであるとする.決定制約は次のようになる:
は非零となるような決定ベクトルであるとする.決定制約は次のようになる:
![]() のときの制約
のときの制約 ![]() をモデル化するために,
をモデル化するために,![]() となるような大きい定数
となるような大きい定数 ![]() を選ぶ:
を選ぶ:
補助変数 ![]() を使うと,目的は
を使うと,目的は![]() となるように
となるように ![]() を最小化することに変わる.これは
を最小化することに変わる.これは![]() に等しい:
に等しい:
部分集合の選択は,Fitで ![]() 正規化を使うとより効率よくできる.まず,最高で
正規化を使うとより効率よくできる.まず,最高で ![]() 個の基底関数を使う正規化パラメータの範囲を求める:
個の基底関数を使う正規化パラメータの範囲を求める:
関数集合候補から与えられたデータを近似する関数の最良の部分集合を求める:
幾何問題 (6)
![]() を中心として半径
を中心として半径 ![]() で,点の集合を包含している最小の円板を求める:
で,点の集合を包含している最小の円板を求める:
各点 ![]() について,制約条件
について,制約条件 ![]() が満足されなければならない.この条件は
が満足されなければならない.この条件は![]() に等しい.条件の立式にはInactiveを使う:
に等しい.条件の立式にはInactiveを使う:
境界円板の最小面積はBoundingRegionを使って求めることもできる:
![]() としてパラメータ化された,点の集合を取り囲む最小楕円を,面積を最小化することで求める:
としてパラメータ化された,点の集合を取り囲む最小楕円を,面積を最小化することで求める:
この面積は ![]() に比例する.単調関数Logを適用すると,最小化する関数は
に比例する.単調関数Logを適用すると,最小化する関数は![]() になる.これは,
になる.これは,![]() を最小化することに等しい:
を最小化することに等しい:
境界楕円は,最小面積であるとは限らないが,BoundingRegionを使って求めることができる:
![]() としてパラメータ化された,点の集合を取り囲む三次元で最小の楕円を,体積を最小にすることで求める:
としてパラメータ化された,点の集合を取り囲む三次元で最小の楕円を,体積を最小にすることで求める:
体積を最小化することは,![]() を最小化することに等しいが,これは
を最小化することに等しいが,これは![]() を最小化することに等しい:
を最小化することに等しい:
境界楕円体は,体積が最小であるとは限らないが,BoundingRegionを使って求めることができる:
![]() としてパラメータ化された,凸多角形にフィットする最大面積の楕円を求める:
としてパラメータ化された,凸多角形にフィットする最大面積の楕円を求める:
半平面を媒介変数を使って表示すると![]() になる.この項
になる.この項![]() .したがって,制約条件は
.したがって,制約条件は![]() であるが,これは
であるが,これは![]() に等しい:
に等しい:
面積を最小化することは![]() を最小化することに等しいが,これは
を最小化することに等しいが,これは![]() を最小化することに等しい:
を最小化することに等しい:
![]() で与えられる,
で与えられる,![]() の形の3つの楕円を取り囲む円板の中心
の形の3つの楕円を取り囲む円板の中心 ![]() と半径
と半径 ![]() を求める:
を求める:
S-procedureを使うと,円板は![]() のときかつそのときに限り楕円を含むことを示すことができる:
のときかつそのときに限り楕円を含むことを示すことができる:
目的は,![]() で与えられる半径
で与えられる半径 ![]() を最小化することである.補助変数
を最小化することである.補助変数 ![]() を使うと,目的が
を使うと,目的が ![]() となるように
となるように ![]() を最小化することになる.これは,
を最小化することになる.これは,![]() として書くことができる:
として書くことができる:
楕円体が ![]() の形式の他の楕円体の部分集合かどうかをテストする:
の形式の他の楕円体の部分集合かどうかをテストする:
S-procedureを使うと,![]() のときかつそのときに限り楕円2が楕円1の部分集合であることが示せる:
のときかつそのときに限り楕円2が楕円1の部分集合であることが示せる:
楕円体を明示的な形式に変換し,楕円2が楕円1の中にあることを確認する:
テストは,楕円体2が楕円体1の部分集合ではなく,問題が実行不可能であることを示している:
分類問題 (2)
グラフ問題 (3)
半定値最適化を使って計算可能なLovász数は,グラフ不変量をハード計算するための境界として使われる:
Lovász数は,グラフのシャノン(Shannon)容量の上界である:
グラフ ![]() のLovász数
のLovász数 ![]() は
は ![]() ,によって与えられる.ただし,
,によって与えられる.ただし,![]() について
について ![]() ,
,![]() ,
,![]() である.これは,双対半定値形式で,
である.これは,双対半定値形式で,![]() および
および![]() に従う
に従う ![]() ,
, ![]() として書くことができる.これ以外の場合は0である:
として書くことができる.これ以外の場合は0である:
GraphDataからの厳密なLovász数の値と比較する:
最大カット問題は,![]() からその補集合
からその補集合 ![]() に横断する辺の重みの和
に横断する辺の重みの和 ![]() が最大となるグラフの頂点集合
が最大となるグラフの頂点集合 ![]() の部分集合
の部分集合 ![]() を決定する.
を決定する.![]() について
について ![]() で
で ![]() について
について ![]() とする.
とする.![]() を最大化する.ただし,
を最大化する.ただし,![]() であり,
であり,![]() はグラフのラプラス行列である:
はグラフのラプラス行列である:
より小さいグラフについては,最大カット問題は厳密に解くことができるが,大きいグラフの場合は,一般に問題にNP完全性の複雑さが含まれるので,厳密に解くことは現実的ではない:
この問題は![]() を最小化する.ただし,
を最小化する.ただし,![]() は階数1の対称半正定値行列で,各
は階数1の対称半正定値行列で,各 ![]() について
について![]() で,これは
で,これは ![]() に等しい.ただし,
に等しい.ただし,![]() は
は ![]() 番目の対角位置が1でその他は0の行列である.解を現実的なものとするために,階数1の条件を除去した緩和問題を解く.そのような
番目の対角位置が1でその他は0の行列である.解を現実的なものとするために,階数1の条件を除去した緩和問題を解く.そのような ![]() については,カットはランダムな丸めで構築される.
については,カットはランダムな丸めで構築される.![]() を分解する.
を分解する.![]() は単位ノルムの一様分布に従うランダムなベクトルであり,
は単位ノルムの一様分布に従うランダムなベクトルであり,![]() であるとする.デモ用に,緩和された値,丸めた値,
であるとする.デモ用に,緩和された値,丸めた値,![]() 内の点からなる赤で表示されたグラフを示す関数が定義されている:
内の点からなる赤で表示されたグラフを示す関数が定義されている:
前に示した方法で近似最大カットを求め,厳密な結果と比較する:
ペテルセン(Peterson)グラフについて,緩和アルゴリズムと厳密アルゴリズムの所要時間を比較する:
![]() からその対辺
からその対辺 ![]() までの辺の重みの合計
までの辺の重みの合計 ![]() が最大になるようにして,頂点
が最大になるようにして,頂点 ![]() を持つ指定されたグラフの部分集合
を持つ指定されたグラフの部分集合 ![]() を求める.グラフを指定する:
を求める.グラフを指定する:
制御と動的系の問題 (3)
線形の動的系 ![]() が,任意の初期条件について漸近的に安定であることを示す.この系は,
が,任意の初期条件について漸近的に安定であることを示す.この系は,![]() となるような正定値行列
となるような正定値行列 ![]() が存在するときかつそのときに限り安定であると言われる.ただし,
が存在するときかつそのときに限り安定であると言われる.ただし,![]() はリャプノフ(Lyapunov)関数と呼ばれる:
はリャプノフ(Lyapunov)関数と呼ばれる:
リャプノフ関数 ![]() を微分すると
を微分すると ![]() が与えられる.したがって,安定条件は
が与えられる.したがって,安定条件は ![]() である:
である:
![]() の固有値はすべて負であり,したがって,この行列は負定値行列である.これが,安定性を証明する:
の固有値はすべて負であり,したがって,この行列は負定値行列である.これが,安定性を証明する:
系の解析解は ![]() なので,系が任意の初期条件に従って0に近付くことを数値的に確かめる.シミュレーションに
なので,系が任意の初期条件に従って0に近付くことを数値的に確かめる.シミュレーションに ![]() を使う:
を使う:
リャプノフの安定性定理を使うと,目的は,安定化条件![]() を満足する行列
を満足する行列 ![]() を求めることになる.
を求めることになる.![]() とすると,第1条件は適切な半定値条件
とすると,第1条件は適切な半定値条件 ![]() になる:
になる:
目的は![]() となるような
となるような ![]() を求めることである.ただし,
を求めることである.ただし,![]() は単項式のベクトルである:
は単項式のベクトルである:
構造最適化問題 (1)
片端が壁に固定されていて反対側の負荷に耐えなければならないトラスを,その重みを最低にして設計する:
トラスはリンクとノードを使ってモデル化できる.各ノードはリンクによって近傍ノードに接続されている.ノードの位置 ![]() を指定する:
を指定する:
リンクによって互いに接続しているノードを指定し,各リンクの長さを計算する:
リンクは円筒形の棒である.各リンクは断面が ![]() の棒の集合から形成されなければならない.
の棒の集合から形成されなければならない.![]() を,
を,![]() なら棒
なら棒 ![]() が選ばれるような各リンク
が選ばれるような各リンク ![]() の決定ベクトルとする.こうすると,リンク
の決定ベクトルとする.こうすると,リンク ![]() について面積が
について面積が ![]() で定義される.目的は重みを最低にすることである:
で定義される.目的は重みを最低にすることである:
各リンクについて1本の棒しか選択できない.バイナリ制約は以下の通りである:
この系の剛性行列は ![]() で与えられる.ただし,
で与えられる.ただし,![]() はノードの総数,
はノードの総数,![]() は固定されたノード数,
は固定されたノード数,![]() はすべてのリンクの集合である.ベクトルは,
はすべてのリンクの集合である.ベクトルは,![]() なら
なら ![]() ,
,![]() なら
なら ![]() ,それ以外は0である:
,それ以外は0である:
![]() が系全体の力ベクトルであるとする.固定されていない各ノードにおける力は
が系全体の力ベクトルであるとする.固定されていない各ノードにおける力は ![]() である.力が適用されるノードは
である.力が適用されるノードは ![]() である:
である:
![]() を任意のノードにおける最大許容たわみとし,
を任意のノードにおける最大許容たわみとし,![]() をノード
をノード ![]() の変位とすると,
の変位とすると,![]() なら
なら ![]() が満足される.ただし,
が満足される.ただし,![]() はリンク
はリンク ![]() に関連付けられた剛性行列である:
に関連付けられた剛性行列である:
特性と関係 (8)
SemidefiniteOptimizationは目的関数の大域的最小値を与える:
Minimizeは,半定値問題に対して大域的な厳密結果を与える:
SemidefiniteOptimizationと比較する:
NMinimizeを使って,大域メソッドによって厳密ではない結果を得ることができる:
FindMinimumを使って,局所メソッドによって厳密ではない結果を得ることができる:
ConicOptimizationはSemidefiniteOptimizationよりも一般的である:
SecondOrderConeOptimizationはSemidefiniteOptimizationの特殊ケースである:
QuadraticOptimizationはSemidefiniteOptimizationの特殊ケースである:
補助変数 ![]() を使い,追加的な制約条件
を使い,追加的な制約条件![]() を使って
を使って ![]() を最小化する:
を最小化する:
LinearOptimizationはSemidefiniteOptimizationの特殊ケースである:
考えられる問題 (5)
デフォルトオプションでは,この制約条件は許容度10-8に違反する:
ミニマイザはIndeterminateである:
ミニマイザはIndeterminateである:
混合整数問題についての双対に関連した解の特性は得られないかもしれない:
制約条件の行列はエルミート行列でよいが,変数は実数でなければならない:

Vectors[n]を評価すると自動的にVectors[n,Complexes]になる:
指定に複素数を含まない問題については,ベクトル変数 v ∈Vectors[n]は実数値であるとみなされる.その他の場合は,Vectors[n,Reals]として明示的に領域を与えなければならない:
テキスト
Wolfram Research (2019), SemidefiniteOptimization, Wolfram言語関数, https://reference.wolfram.com/language/ref/SemidefiniteOptimization.html (2020年に更新).
CMS
Wolfram Language. 2019. "SemidefiniteOptimization." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/SemidefiniteOptimization.html.
APA
Wolfram Language. (2019). SemidefiniteOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SemidefiniteOptimization.html
