SemidefiniteOptimization[f,cons,vars]
求可最小化受半定约束条件 cons 限制的线性目标函数 f 的变量 vars 的值.
SemidefiniteOptimization[c,{a0,a1,…,ak}]
求可最小化受线性矩阵不等式约束条件 ![]() 限制的量
限制的量 ![]() 的向量
的向量 ![]() .
.
SemidefiniteOptimization[…,"prop"]
指定应返回解的属性 "prop".




SemidefiniteOptimization
SemidefiniteOptimization[f,cons,vars]
求可最小化受半定约束条件 cons 限制的线性目标函数 f 的变量 vars 的值.
SemidefiniteOptimization[c,{a0,a1,…,ak}]
求可最小化受线性矩阵不等式约束条件 ![]() 限制的量
限制的量 ![]() 的向量
的向量 ![]() .
.
SemidefiniteOptimization[…,"prop"]
指定应返回解的属性 "prop".
更多信息和选项






- SemidefiniteOptimization 亦称为半定规划 (SDP) 和混合整数半定规划 (MISDP).
- 半定优化是一种凸优化问题,可以用实数、整数或复变量高效全局求解.
- 半定优化求的是能解原始问题的
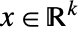 :
: -
最小化 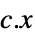
受限于约束条件 ![a_(0)+a_(1) x_(1)+...+a_(k) x_(k)>=_(TemplateBox[{n}, SemidefiniteConeList])0 a_(0)+a_(1) x_(1)+...+a_(k) x_(k)>=_(TemplateBox[{n}, SemidefiniteConeList])0](Files/SemidefiniteOptimization.zh/6.png)
其中 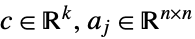
- 矩阵
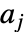 必须是对称的
必须是对称的 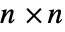 矩阵.
矩阵. - 混合整数半定优化求能解以下问题的
 和
和 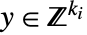 :
: -
最小化 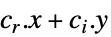
受限于约束条件 ![a_(0)+a_(1) x_(1)+...+a_(k_r) x_(k_r)+a_(k_r+1)y_1+...+a_(k_r+k_i)y_(k_i)>=_(TemplateBox[{n}, SemidefiniteConeList])0 a_(0)+a_(1) x_(1)+...+a_(k_r) x_(k_r)+a_(k_r+1)y_1+...+a_(k_r+k_i)y_(k_i)>=_(TemplateBox[{n}, SemidefiniteConeList])0](Files/SemidefiniteOptimization.zh/13.png)
其中 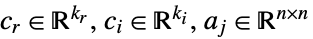
- 当目标函数为实数时,SemidefiniteOptimization 通过在内部将
![x in TemplateBox[{}, Complexes]^n x in TemplateBox[{}, Complexes]^n](Files/SemidefiniteOptimization.zh/15.png) 转换为实变量
转换为实变量  来求解,其中
来求解,其中 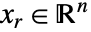 和
和 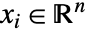 . 可以用埃尔米特矩阵
. 可以用埃尔米特矩阵  指定线性矩阵不等式.
指定线性矩阵不等式. - 变量指定 vars 应该是一个列表,其中的元素按以下形式给出变量:
-
v 名称为  的变量,维度由推断而得
的变量,维度由推断而得v∈Reals 实标量变量 v∈Integers 整数标量变量 v∈Complexes 复标量变量 v∈ℛ 仅限于几何区域 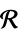 的向量变量
的向量变量v∈Vectors[n,dom] 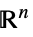 或
或 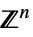 中的向量变量
中的向量变量v∈Matrices[{m,n},dom] 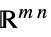 或
或  中的矩阵变量
中的矩阵变量 - 可用以下形式指定约束条件 cons:
-
LessEqual 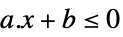
标量不等式 GreaterEqual 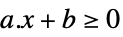
标量不等式 VectorLessEqual 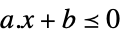
向量不等式 VectorGreaterEqual 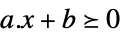
向量不等式 Equal 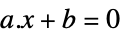
标量或向量等式 Element 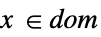
凸域或区域元素 - 对于 SemidefiniteOptimization[f,cons,vars],可在约束条件中包括形式为 parval 的参数方程,以定义在 f 或 cons 中使用的参数,其中 par 不在 vars 中,val 是数值或数值数组. »
- 原始最小化问题有相关的最大化问题,即拉格朗日对偶问题. 对偶最大值始终小于或等于原始最小值,因此它给出了下限. 对偶最大值点提供了有关原始问题的信息,包括最小值对约束条件变化的敏感性. »
- 半定优化有对偶问题: »
-
最大化 ![-TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {2ColumnTableMod}][a_0.lambda] -TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {2ColumnTableMod}][a_0.lambda]](Files/SemidefiniteOptimization.zh/33.png)
受限于约束条件 ![TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {2ColumnTableMod}][a_j.lambda]=c_j,j=1,..., k,lambda>=_(TemplateBox[{n}, SemidefiniteConeList])0 TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {2ColumnTableMod}][a_j.lambda]=c_j,j=1,..., k,lambda>=_(TemplateBox[{n}, SemidefiniteConeList])0](Files/SemidefiniteOptimization.zh/34.png)
其中 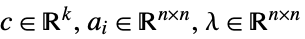
- 可能的解的属性 "prop" 包括:
-
"PrimalMinimizer" 
一个最小化目标函数的变量值列表 "PrimalMinimizerRules" 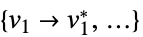
最小化 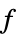 的变量值 vars={v1,…}
的变量值 vars={v1,…}"PrimalMinimizerVector" 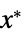
最小化 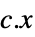 的向量
的向量"PrimalMinimumValue" 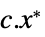
原始最小值 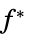
"DualMaximizer" 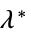
最大化 ![-TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {3ColumnTableMod}][a_0.lambda] -TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {3ColumnTableMod}][a_0.lambda]](Files/SemidefiniteOptimization.zh/44.png) 的矩阵
的矩阵"DualMaximumValue" ![-TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {3ColumnTableMod}][a_0.lambda^*] -TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {3ColumnTableMod}][a_0.lambda^*]](Files/SemidefiniteOptimization.zh/45.png)
对偶最大值 "DualityGap" ![-TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {3ColumnTableMod}][a_0.lambda^*] - c.x^* -TemplateBox[{Tr, paclet:ref/Tr}, RefLink, BaseStyle -> {3ColumnTableMod}][a_0.lambda^*] - c.x^*](Files/SemidefiniteOptimization.zh/46.png)
对偶值和原始最优值之间的差 "Slack" 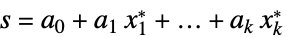
把不等式约束条件转换成等式的矩阵 "ConstraintSensitivity" 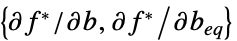
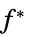 对约束条件扰动的敏感度
对约束条件扰动的敏感度"ObjectiveVector" 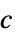
线性目标向量 "ConstraintMatrices" 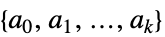
约束矩阵列表 {"prop1","prop2",…} 解的几个属性 - 可给出以下选项:
-
MaxIterations Automatic 使用的最大迭代次数 Method Automatic 使用的方法 PerformanceGoal $PerformanceGoal 优化的目标 Tolerance Automatic 内部比较使用的误差 - 选项 Method->method 可用于指定使用的方法. 可用的方法包括:
-
Automatic 自动选择方法 "CSDP" CSDP 半定优化求解器 "DSDP" DSDP 半定优化求解器 "SCS" SCS 分裂圆锥求解器 "MOSEK" 商用 MOSEK 凸优化求解器 - 计算受限于 MachinePrecision.
范例
打开所有单元 关闭所有单元基本范例 (3)
范围 (29)
基本用途 (13)
使用向量变量 ![]() 和 Inactive[Plus] 避免意外的线程:
和 Inactive[Plus] 避免意外的线程:
使用向量变量 ![]() 和 Indexed[x,i] 指定单个分量:
和 Indexed[x,i] 指定单个分量:
在不明确时,使用 Vectors[n] 指定向量变量的维度:
多个线性不等式约束可用 VectorGreaterEqual 表示:
使用 ![]() v>=
v>=![]() 或 \[VectorGreaterEqual] 输入向量不等式符号 :
或 \[VectorGreaterEqual] 输入向量不等式符号 :
使用 NonNegativeReals (![]() ) 指定非负约束:
) 指定非负约束:
整数变量 (4)
使用 Integers 指定整数域约束:
使用 Vectors[n,Integers] 指定向量变量的整数域约束:
使用 NonNegativeIntegers (![]() ) 指定非负整数域约束:
) 指定非负整数域约束:
使用 NonPositiveIntegers (![]() ) 指定非正整数域约束:
) 指定非正整数域约束:
复数变量 (2)
原始模型属性 (3)
对偶模型属性 (3)
选项 (8)
Method (5)
当默认方法 "CSDP" 产生一条信息,首先尝试 "DSDP":
带有 10-3 默认容差的 "SCS" 是另一种可尝试的方法:
"SCS" 的结果质量通常可以通过较小的 Tolerance 来改善:
PerformanceGoal (1)
选项 PerformanceGoal 的默认值是 $PerformanceGoal:
使用 PerformanceGoal"Quality" 获取更精确的结果:
使用 PerformanceGoal"Speed" 更快获取结果,但代价是质量:
应用 (33)
基本的模型变换 (13)
求最小化对称矩阵的最大特征值的 ![]() ,对称矩阵线性依赖于决策变量
,对称矩阵线性依赖于决策变量 ![]() ,
, ![]() . 该问题可以作为线性矩阵不等式被公式化,因为
. 该问题可以作为线性矩阵不等式被公式化,因为 ![]() 等价于
等价于 ![]() ,其中,
,其中,![]() 是
是 ![]() 的第
的第 ![]()
![]() 个特征值. 定义线性矩阵函数
个特征值. 定义线性矩阵函数 ![]() :
:
实对称矩阵 ![]() 可用正交矩阵
可用正交矩阵 ![]() 对角化,所以
对角化,所以 ![]() . 因此
. 因此 ![]() 当且仅当
当且仅当 ![]() . 既然,任何
. 既然,任何 ![]() 都接受
都接受 ![]() ,
,![]() ,因此
,因此 ![]() 当且仅当
当且仅当 ![]() . 数值模拟显示这些公式是等价的:
. 数值模拟显示这些公式是等价的:
求最大化对称矩阵 ![]() 最小特征值的
最小特征值的 ![]() ,对称矩阵线性依赖于决策变量
,对称矩阵线性依赖于决策变量 ![]() . 定义线性矩阵函数
. 定义线性矩阵函数 ![]() :
:
问题可以作为线性矩阵不等式被公式化,因为 ![]() 等价于
等价于 ![]() ,其中,
,其中,![]() 是
是 ![]() 的第
的第 ![]()
![]() 个特征值. 为了最大化
个特征值. 为了最大化 ![]() ,先最小化
,先最小化 ![]() :
:
求最小化对称矩阵 ![]() 的最大和最小特征值之间差的
的最大和最小特征值之间差的 ![]() ,对称矩阵线性依赖于决策变量
,对称矩阵线性依赖于决策变量 ![]() . 定义线性矩阵函数
. 定义线性矩阵函数 ![]() :
:
该问题可以作为线性矩阵不等式被公式化,因为 ![]() 等价于
等价于 ![]() ,其中,
,其中,![]() 是
是 ![]() 的第
的第 ![]()
![]() 个特征值. 求解由此产生的问题:
个特征值. 求解由此产生的问题:
最大的特征值满足 ![]() 最大绝对值的负
最大绝对值的负 ![]() 特征值是最大的
特征值是最大的 ![]() 特征值并满足
特征值并满足 ![]() :
:
![]() 的最大奇异值
的最大奇异值 ![]() 是
是 ![]() 最大特征值的平方根,而且根据前面的例子,它满足
最大特征值的平方根,而且根据前面的例子,它满足 ![]() 或等价于
或等价于 ![]() :
:
最小化 ![]() . 使用辅助变量
. 使用辅助变量 ![]() ,把问题转换为最小化
,把问题转换为最小化 ![]() ,因此
,因此 ![]() . 这个与
. 这个与 ![]() 一样:
一样:
Schur 补充条件表示,如果 ![]() ,则块矩阵
,则块矩阵 ![]() 当且仅当
当且仅当 ![]() . 因此,当
. 因此,当 ![]() ,
,![]() ⧦
⧦ ![]() ,当
,当 ![]() ,使得
,使得 ![]() 必须为 0:
必须为 0:
最小化 ![]() 受限于
受限于 ![]() ,假设
,假设 ![]() ,当
,当 ![]() . 使用辅助变量
. 使用辅助变量 ![]() ,目标是最小化
,目标是最小化 ![]() ,使得
,使得 ![]() :
:
使用 Schur 补充条件,![]() 当且仅当
当且仅当 ![]() . 使用 Inactive[Plus] 构建约束避免线程:
. 使用 Inactive[Plus] 构建约束避免线程:
对于二次集 ![]() ,其包括椭球、二次锥和抛物线,确定是否
,其包括椭球、二次锥和抛物线,确定是否 ![]() ,其中,
,其中,![]() 是对称矩阵,
是对称矩阵,![]() 是向量,
是向量,![]() 是标量:
是标量:
假设集合 ![]() 是全维的,S-进程表明
是全维的,S-进程表明 ![]() 当且仅当存在一些非负数
当且仅当存在一些非负数 ![]() 使得
使得 ![]() 视觉上存在非负
视觉上存在非负 ![]() :
:
最小化 ![]() 受限于
受限于 ![]() . 把目标
. 把目标 ![]() 转换成带有额外约束
转换成带有额外约束 ![]() 的线性函数
的线性函数 ![]() ,其等于
,其等于 ![]() :
:
最小化 ![]() 受限于
受限于 ![]() . 使用
. 使用 ![]() 和额外约束
和额外约束 ![]() 把目标转换成线性函数:
把目标转换成线性函数:
最小化 ![]() 受限于
受限于 ![]() . 把目标转换成带有额外约束
. 把目标转换成带有额外约束 ![]() 的线性函数
的线性函数 ![]() ,其等于
,其等于 ![]() :
:
数据拟合问题 (5)
选择多项式基并使用 DesignMatrix 构建输入矩阵和输出向量:
使用辅助变量 ![]() ,目标被转换成最小化
,目标被转换成最小化 ![]() 使得
使得 ![]() ,其等于
,其等于 ![]() 如基本模型变换所示:
如基本模型变换所示:
通过使用切比雪夫基最小化 ![]() 找到在对数比例上变化的离散数据的近似函数:
找到在对数比例上变化的离散数据的近似函数:
因为数据是对数比例,直接数据拟合并不理想. 所以把问题转换成最小化 ![]() . 使用辅助变量
. 使用辅助变量 ![]() ,最小化
,最小化 ![]() 使得
使得 ![]() . 该约束等价于
. 该约束等价于 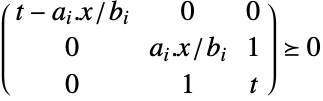 :
:
数据拟合可以直接使用 Fit 获得. 然而,没有对数转换的话在近似函数中会有显著的振荡:
二次项 ![]() ,其中,
,其中,![]() 是从
是从 ![]() 的 Cholesky 分解获得的下三角矩阵:
的 Cholesky 分解获得的下三角矩阵:
也可以用 Fit 通过 ![]() 正则化更高效地完成子集选择. 首先,找到最多使用
正则化更高效地完成子集选择. 首先,找到最多使用 ![]() 个基函数的正则化参数的范围:
个基函数的正则化参数的范围:
几何问题 (6)
对于每个点 ![]() ,必须满足约束条件
,必须满足约束条件 ![]() . 该约束条件等价于
. 该约束条件等价于 ![]() . 在构建约束条件时使用 Inactive:
. 在构建约束条件时使用 Inactive:
可通过 BoundingRegion 找到面积最小的包围圆盘:
面积与 ![]() 成正比. 应用单调函数 Log,要最小化的函数变为
成正比. 应用单调函数 Log,要最小化的函数变为 ![]() . 这相当于最小化
. 这相当于最小化 ![]() :
:
可以用 BoundingRegion 求边界椭圆(面积不一定最小):
可以用 BoundingRegion 求边界椭球(体积不一定最小):
把参数化应用到半平面给出 ![]() . 其中
. 其中 ![]() . 因此,约束条件为
. 因此,约束条件为 ![]() ,它等价于
,它等价于 ![]() :
:
求由 ![]() 给定的包围三个椭圆(形式为
给定的包围三个椭圆(形式为 ![]() )的圆盘的中心
)的圆盘的中心 ![]() 和半径
和半径 ![]() :
:
通过 S-procedure,可得出当且仅当 ![]() ,圆盘才包含椭圆:
,圆盘才包含椭圆:
目的是最小化由 ![]() 给定的半径
给定的半径 ![]() . 使用辅助变量
. 使用辅助变量 ![]() ,目标变为最小化使得
,目标变为最小化使得 ![]() 的
的 ![]() ,可以写为
,可以写为 ![]() :
:
通过 S-procedure,可得出当且仅当 ![]() ,椭圆 2 才是椭圆 1 的子集::
,椭圆 2 才是椭圆 1 的子集::
测试显示问题是不可行的,表明椭球 2 不是椭球 1 的子集:
分类问题 (2)
图问题 (3)
使用半定优化可计算的 Lovász 数被用作硬计算图不变量的边界:
图 ![]() 的 Lovász 数
的 Lovász 数 ![]() 由
由 ![]() 给出,其中,
给出,其中,![]() ,对于
,对于 ![]() ,
,![]() 且
且 ![]() . 可以写成对偶半定格式:
. 可以写成对偶半定格式:![]() ,
, ![]() ,受限于
,受限于 ![]() 和
和 ![]() ,否则为 0:
,否则为 0:
比较 GraphData 中确切的 Lovász 数值:
矩阵切割问题确定图的顶点 ![]() 的子集
的子集 ![]() ,从
,从 ![]() 跨到补集
跨到补集 ![]() 的边的权重
的边的权重 ![]() 之和被最大化. 对于
之和被最大化. 对于 ![]() ,让
,让 ![]() ,对于
,对于 ![]() ,让
,让 ![]() . 最大化
. 最大化 ![]() ,其中,
,其中,![]() 和
和 ![]() 是图的拉普拉斯矩阵:
是图的拉普拉斯矩阵:
对于较小的情况,最大切割问题可以被精确地解决,但是对于较大的图来说,这是不切实际的,因为一般来说,这个问题具有NP-完备复杂度:
问题最小化 ![]() ,其中,
,其中,![]() 是对称秩-1正半定矩阵,对于每个
是对称秩-1正半定矩阵,对于每个 ![]() ,
,![]() ,等价于
,等价于 ![]() ,其中,
,其中,![]() 是在第
是在第 ![]() 个对角位置为 1 ,其他为 0 的矩阵. 为了使解决方案切实可行,求解松弛问题,其中,秩-1 条件被消除. 对于该
个对角位置为 1 ,其他为 0 的矩阵. 为了使解决方案切实可行,求解松弛问题,其中,秩-1 条件被消除. 对于该 ![]() ,通过随机舍入构建切割: 分解
,通过随机舍入构建切割: 分解 ![]() ,令
,令 ![]() 是单位范数的均匀分布的随机向量,并且令
是单位范数的均匀分布的随机向量,并且令 ![]() . 对于演示,显示松驰值的函数被定义,
. 对于演示,显示松驰值的函数被定义,![]() 中舍入值和带有顶点的图显示为红色:
中舍入值和带有顶点的图显示为红色:
求指定的图(顶点为 ![]() )的子集
)的子集 ![]() ,使得从
,使得从 ![]() 到补集
到补集 ![]() 的边的权重
的边的权重 ![]() 的和最大化. 指定图:
的和最大化. 指定图:
目标是最大化 ![]() ,其中
,其中 ![]() 是对称的 rank-1 正半定矩阵,
是对称的 rank-1 正半定矩阵,![]() 是图的拉普拉斯矩阵:
是图的拉普拉斯矩阵:
控制和动力系统问题 (3)
结构优化问题 (1)
设计一个最小重量的桁架,一端固定在墙上,必须能够承受另一端的负载:
可以用 link 和节点对桁架进行建模. 每个节点通过 link 连接到相邻节点. 指定节点位置 ![]() :
:
指定通过 link 相互连接的节点,并计算每个 link 的长度:
link 为圆杆. 每个 link 必须从一组横截面为 ![]() 的圆杆中选择. 设
的圆杆中选择. 设 ![]() 为每个link
为每个link ![]() 的决策变量,如果
的决策变量,如果 ![]() ,则圆杆
,则圆杆 ![]() 被选中. 对于 link
被选中. 对于 link ![]() ,面积被定义为
,面积被定义为 ![]() . 目标是最小化重量:
. 目标是最小化重量:
系统的刚度矩阵由 ![]() 给出,其中
给出,其中 ![]() 是节点的总数,
是节点的总数,![]() 是锚定的节点的数量,
是锚定的节点的数量,![]() 是所有 link 的集合. 如果
是所有 link 的集合. 如果 ![]() ,向量
,向量 ![]() ;如果
;如果 ![]() ,
,![]() ,否则为 0:
,否则为 0:
设 ![]() 为整个系统的受力向量. 在每个没有被锚定的节点处,受力为
为整个系统的受力向量. 在每个没有被锚定的节点处,受力为 ![]() . 在节点
. 在节点 ![]() 处施加力:
处施加力:
属性和关系 (8)
SemidefiniteOptimization 给出了目标函数的全局最小值:
Minimize 为半定问题提供全局精确结果:
与 SemidefiniteOptimization 相比:
NMinimize 用于使用全局方法获得不精确的结果:
FindMinimum 可用于使用局部方法获取不精确的结果:
ConicOptimization 比 SemidefiniteOptimization 更通用:
SecondOrderConeOptimization 是 SemidefiniteOptimization 的一个特例:
可能存在的问题 (5)
最小值点是 Indeterminate:
最小值点是 Indeterminate:
Vectors[n] 自动运算为 Vectors[n,Complexes]:
对于规范中没有复数的问题,向量变量 v ∈Vectors[n] 被认为是实值的;否则,您需要明确地将域指定为 Vectors[n,Reals]:
相关指南
-
▪
- 凸优化 ▪
- 基于矩阵的最小化 ▪
- 最优化 ▪
- 符号向量、矩阵和数组
文本
Wolfram Research (2019),SemidefiniteOptimization,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SemidefiniteOptimization.html (更新于 2020 年).
CMS
Wolfram 语言. 2019. "SemidefiniteOptimization." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/SemidefiniteOptimization.html.
APA
Wolfram 语言. (2019). SemidefiniteOptimization. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SemidefiniteOptimization.html 年
BibTeX
@misc{reference.wolfram_2025_semidefiniteoptimization, author="Wolfram Research", title="{SemidefiniteOptimization}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/SemidefiniteOptimization.html}", note=[Accessed: 03-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_semidefiniteoptimization, organization={Wolfram Research}, title={SemidefiniteOptimization}, year={2020}, url={https://reference.wolfram.com/language/ref/SemidefiniteOptimization.html}, note=[Accessed: 03-February-2026]}
