TrimmedVariance

TrimmedVariance[list,f]

割合 f の最小および最大要素を除いた後の list 中の要素の分散を与える．

TrimmedVariance[list,{f1,f2}]

割合 f1の最小要素と割合 f2の最大要素を除いたときの分散を与える．

TrimmedVariance[list]

5%刈込み分散TrimmedVariance[list,0.05]を与える．

TrimmedVariance[dist,…]

一変量分布 dist の刈込み分散を与える．

詳細

  • TrimmedVarianceは，極値を除くことで分散のロバスト推定を与える．
  • 刈込みの割合はパラメータ f1とパラメータ f2で決定される．これは，割合 f1の最小要素と割合 f2の最大要素が取り除かれることを意味する．
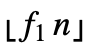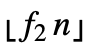  • TrimmedVariance[list,{f1,f2}]はSort[list,Less]〚1+;;n-〛の分散を与える．ただし，n は list の長さに等しい．
  • TrimmedVariance[{{x1,y1,…},{x2,y2,…},…},f]は{TrimmedVariance[{x1,x2,…},f],TrimmedVariance[{y1,y2,…},f],…}を与える．
  • TrimmedVariance[dist,{f1,f2}]は，一変量分布 dist について，Variance[TruncatedDistribution[Quantile[dist,{f1,1-f2}],dist]]を与える．

例題

すべて開くすべて閉じる

例  (4)

極値を除いた後の刈込み分散：

最小極値を除いた後の刈込み分散：

日付のリストの刈込み分散：

記号分布の刈込み分散：

スコープ  (10)

データ  (9)

厳密な入力は厳密は出力を与える：

近似入力は近似出力を与える：

行列についてのTrimmedVarianceは列ごとの分散を与える：

刈込み分散は大きい配列に使うことができる：

SparseArrayデータは密な配列と同じように使うことができる：

TimeSeriesの刈込み分散：

刈込み分散は値のみに依存する：

刈込み分散は単位付き数量を含むデータに使うことができる：

日付の刈込み分散を計算する：

時間の刈込み分散を計算する：

異なる時刻帯指定の時刻のリスト：

分布  (1)

一変量分布の刈込み分散：

アプリケーション  (2)

外れ値がある場合の分散についてのロバスト推定を得る：

極値はVarianceに大きく影響する：

学級の生徒の身長についての刈込み分散を求める：

刈込み分散を刈込み割合の関数としてプロットする：

刈込み平均についての刈込み分散の平方根をプロットする：

特性と関係  (5)

0%TrimmedVarianceはVarianceに等しい：

f が1/2に近付くにつれてTrimmedVarianceは0に近付く：

分布のTrimmedVarianceはそのTruncatedDistributionの分散である：

適切な境界があるTruncatedDistributionの分散：

サンプルのTrimmedVarianceは切断分布の分散推定を与える：

適切な境界があるTruncatedDistributionの分散：

TrimmedVarianceは特定の分位レベルを超えるデータを削除し，次にサンプル分散を計算する：

WinsorizedVarianceは特定の分位レベルを超えるデータを切り取り，次にサンプル分散を計算する：

ソートされたデータを，要素が取り除かれたサンプルおよび要素が切り取られたサンプルとともにプロットする：

考えられる問題  (1)

TrimmedVarianceには数値が必要である：

Wolfram Research (2017), TrimmedVariance, Wolfram言語関数， https://reference.wolfram.com/language/ref/TrimmedVariance.html （2024年に更新）.

テキスト

Wolfram Research (2017), TrimmedVariance, Wolfram言語関数， https://reference.wolfram.com/language/ref/TrimmedVariance.html （2024年に更新）.

CMS

Wolfram Language. 2017. "TrimmedVariance." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/TrimmedVariance.html.

APA

Wolfram Language. (2017). TrimmedVariance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TrimmedVariance.html

BibTeX

@misc{reference.wolfram_2024_trimmedvariance, author="Wolfram Research", title="{TrimmedVariance}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/TrimmedVariance.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_trimmedvariance, organization={Wolfram Research}, title={TrimmedVariance}, year={2024}, url={https://reference.wolfram.com/language/ref/TrimmedVariance.html}, note=[Accessed: 21-November-2024 ]}