代数計算の基礎
「数の四則演算」の一覧にある演算子で記述できる代数式は何でも入力することができる．掛け算はスペースで表す．xyの掛け算ではスペースを入れるのを忘れないようにしてほしい．xyとスペースを入れないで続けてタイプしてしまうと，変数xと変数yの積ではなくて，名前がxyの単一のシンボルとして解釈されてしまう．
関数Expandを使うと，乗算とベキの項が展開される：
複雑な式を入力するときは，丸カッコの使い方とその挿入位置が重要になる．つまり，例えば，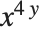
を記述するにはx^(4y)と入力しなければならない．ここでもし丸カッコを入れないと，
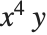になってしまう．カッコは入れすぎても別に問題にはならないから，なるべく使った方がよい．カッコの効果的な使い方に関しては，「演算子の入力形」に説明があるのでそちらを参照のこと．
を記述するにはx^(4y)と入力しなければならない．ここでもし丸カッコを入れないと， になってしまう．カッコは入れすぎても別に問題にはならないから，なるべく使った方がよい．カッコの効果的な使い方に関しては，「演算子の入力形」に説明があるのでそちらを参照のこと．式が入力されると，式を変形するためにWolframシステムが自動的にその膨大なライブラリにある変換規則を次々に式に適用する．これらの変換規則には，代数学の標準的な規則（例えば，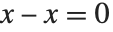
），および高等数学の関数で使われる高度な規則が含まれる．
），および高等数学の関数で使われる高度な規則が含まれる．
Wolframシステムの動作原理は極めて単純で，次のように表すことができる．つまり，入力された式は何でも受け入れ，変換規則を次々に適用していくことで式を適当な形に変形する．適用可能な変換規則を使い果たした時点で，処理を停止し，変形した式を結果として出力する．
1つの代数式は普通いくつもの形で表すことができる．例えば，式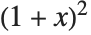
は，
と書いても同じである．Wolframシステムには代数式の変形のための関数が各種用意されており，それらを使い代数式を異なった形に変えることができる．
は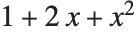，と書いても同じである．Wolframシステムには代数式の変形のための関数が各種用意されており，それらを使い代数式を異なった形に変えることができる．Expandは，積とベキ乗の項を展開し，いわゆる「展開式」を与える：
Factorでもとの式に戻る：
Expandを使うと複雑な式が生成されてしまうことがある：
Factorを使うと通常は簡単な式が得られる：
しかしこの例のように，式によっては，Factorを使うとかえって複雑な式になってしまうことがある：
この場合は，Expandを使った方が「より簡単」な式が得られる：
代数式をできる限り簡単な形で表現したいと思うときがよくある．しかし，「簡単な形」と一概にいっても，どう変形したら実際に簡単になるか，の疑問をすべてのケースではっきりさせるのはなかなか難しい．これを実際に行う手順として，式をいろいろな形に書き直してみて，その中で一番項数が少ない形を選ぶ方法が実践的でよいだろう．
| Simplify[expr] | 標準的な代数変形を適用して，式 expr の最も簡単な形を探す |
| FullSimplify[expr] | 標準外の広範な変形を使い最も簡単な形を探す |
Simplifyを頻繁に使うことで，計算で得られる結果を「整理」しておくことができる．
Integrateの結果を微分するともとの積分式が得られるはずである．こういうことはよくあるが，この場合は，もっと複雑な式になってしまう：
ここでもSimplifyを使うと，もとのより分かりやすい形を取り戻すことができる：
Simplifyは，与えられた式に対して各種の標準的な代数変形を試すように設定されている．ただし，式によってはもっと高等な変形を使い簡約化が進められる場合もある．
FullSimplifyは，さらに多くの変形を試すようにできている．これらの変形では，代数関数だけでなく他の多種に渡る関数が使われる．
Simplifyでは式を簡約することができない：
そこで，FullSimplifyを使ってみると，より簡単な形に変形できる：
式が短い場合は，FullSimplifyで驚くほど簡単な式を得られることがよくある．しかし，式が長くなると，処理スピードが極端に落ちてしまうことがある．
スピード低下の原因はFullSimplifyの処理手順にある．つまり，式から項を代る代るに取り出しては，その項以外の項に1つずつ組み合せていき，その結果得られる各々の組に対して変形が試されるからである．もとの式が大きいと天文学的な回数が必要になってしまう．
Simplifyも難しい処理を行わなければならないが，FullSimplifyが試すような処理に非常に長い時間がかかる変形は避けるように設定されている．簡単な代数計算なら，Simplifyを逐次適用していくことで得られた結果を順次簡約していけるので便利であろう．
しかし，複雑な計算になると，FullSimplifyはもとより，Simplifyでさえも膨大な数のさまざまな形を試すことで終ってしまい，そのため計算に費やす時間も長くなる．そのような場合は，ユーザが簡約化をきめ細くコントロールし，最終的にどのような形にしたいかということを考えながら，各段階の計算を進める必要がある．
方程式の仮定についての還元の場合のように，SimplifyおよびFullSimplifyにより使われる変換の中には，変数の順序を選ぶ必要があるものもある．したがって，簡約の結果は，シンボルの名前に依存する．
| Expand[expr] | 式の積とベキ乗の項を展開する |
| ExpandAll[expr] | のすべての項にExpandを適用する |
| Factor[expr] | 式を因子の積の形に変換する |
| Together[expr] | 式を通分し単一分数にまとめる |
| Apart[expr] | 式を簡単な形の分母を持った複数の分数項に展開する |
| Cancel[expr] | 式において分母と分子の共通因子を約分する |
| Simplify[expr] | 式 expr に代数変形を試し，最も短い式の形を探す |
Expandは，分子だけを展開する．分母は因数分解された形のまま残される：
ExpandAllは，分母を含むすべての項を展開する：
Togetherは，共通分母ですべての項をまとめる：
Apartは，式を簡単な分母を持つ部分分数にする：
Factorはすべての項を因数分解する．この場合，もとの形の式が得られる：
Simplifyでは，これが式の取り得る最も簡単な形である：
最終的にほしい形に式を持っていくのはある種，芸のようなものである．多くの場合，実験してみるというのが最良の方法である．ほしい形になるまでいろいろ変形を試してみることだ．これを行うのにパレットを利用すると便利である．
式の変数が1つだけならば，式を項の和や積の形やその他の形で表すことができる．式に変数が複数ある場合は，式を表せる形はさらに多くなる．そのようなときは，例えば，主要な変数を選んでおき，その変数を中心に式の項をグループ化することが可能である．
| Collect[expr,x] | x の同じ次数の項をまとめる |
| FactorTerms[expr,x] | x に依存しない因子を取り出す |
以上の例から分かるように，多項式や有理式だけに限っても，非常に多くの形で1つの式を表すことができる．さらに複雑な式の場合，例えば，高等数学の関数を使う場合，可能な形はさらに広がる．しかし，すべての可能な式に対応できるように，限りなくWolfram言語の変換関数を増やすことは不可能である．そこで，Wolfram言語では，ユーザ自身で必要な特殊変換規則を定義できるようにしてある．多くのWolfram言語パッケージでは，この形式による変換規則が使われる．定義の手順に関しては「変換規則と定義」の説明を参照してほしい．
| TrigExpand[expr] | 三角関数の式を項の和の形に展開する |
| TrigFactor[expr] | 三角関数の式を項の積の形に分解する |
| TrigReduce[expr] | 整数倍の角度を用いて三角関数を簡約する |
| TrigToExp[expr] | 三角関数を指数関数に変形する |
| ExpToTrig[expr] | 指数関数を三角関数に変形する |
| FunctionExpand[expr] | 特殊関数やその他の関数を展開する |
| ComplexExpand[expr] | すべての変数が実数からなると前提した上で式を展開する |
| PowerExpand[expr] | 例えば(xy)p を xpyp に展開する |
ExpandやFactor等の関数が返してくる変形は，式中の変数がどんな値を取ろうが常に正しい．しかし，場合によっては，変数が特定の値を取るときだけに有効となるような式の変形が行えると便利である．このような変形を得るための関数のひとつにPowerExpandがある．
PowerExpandを使えば展開される：
| Simplify[expr,assum] | 仮定のもとで式 expr を簡約化 |
| Element[x,dom] | x は領域 dom の要素である |
| Element[{x1,x2,…},dom] | すべての xi は領域 dom の要素である |
| Reals | 実数 |
| Integers | 整数 |
| Primes | 素数 |
| Coefficient[expr,form] | 式 expr に含まれる form の係数を抽出する |
| Exponent[expr,form] | 式 expr に含まれる form の最高次数を抽出する |
| Part[expr,n] または expr[[n]] | 式 expr に含まれる n 番目の項を抽出する |
読者は気付いているかもしれないが，第 n 項の抽出で使われる関数Part[expr,n]は，「リスト要素の操作」で説明したリストの部分抽出で使った関数と同じものである．これは単なる偶然ではない．「式のリスト的操作」で説明するが，実は，すべてのWolfram言語式は，構造上リストと同様に構成されている．しかし，「式のリスト的操作」に示すように注意しなければいけないことがある．Wolfram言語は，代数式を内部で処理する形とは違う形で表示することがあるからである．
Coefficientは，まだ展開されていない多項式に対しても正常に機能する：
| Numerator[expr] | 式 expr の分子を返す |
| Denominator[expr] | 式 expr の分母を返す |
Denominatorを使うと，分母が取り出される：
表示を少なくともっと表示というボタンを使うと，Wolframシステムが式を表示する詳細の程度を減少させたり増加させたりすることができる．全出力を表示ボタンは完全にインターフェースを除去し，完全な結果を表示するが，それにはかなりの時間がかかる場合がある．この機能が動作し始めるデフォルトの閾値は，大きさ制限の設定オプションで設定できる．このボタンは環境設定ダイアログの適切な設定のパネルを開く．
大きい出力の表示を抑える機能は，Wolfram言語関数Shortを使って実装される．直接Shortを使って，式の表示を細かく制御することもできる．また，デフォルトの抑制機能が起動するには十分の大きさでない出力に対して使うこともできる．
| command; | 命令 command を実行するが，結果は表示しない |
| expr//Short | 式 expr の概要を1行分だけ表示する |
| Short[expr,n] | 式 expr の概要を n 行分だけ表示す |