代数计算

符号计算有假设条件的化简
转换代数表达式提取代数表达式的部分内容
化简代数表达式控制大型表达式的显示
将表达式写成不同的形式
符号计算
Wolfram 系统的重要特征之一是它可以进行符号以及数值计算. 这意味着它可以处理代数公式以及数字.
下面是常见的数值计算：
下面是符号计算：
数值计算
符号计算
数值和符号计算.
可以在 Wolfram 系统中键入任何代数表达式：
Wolfram 系统自动执行基本的代数化简. 此处合并 和 得到 ：
可以使用“算术”中列出的运算符键入任意代数表达式. 可以用空格来表示乘法. 注意不要忘记 xy 中的空格. 如果输入的 xy 不带空格，则 Wolfram 语言会将其解释为名称为 xy 的一个符号，而不是两个符号 x 和 y 的乘积.
Wolfram 系统使用标准的代数规则将各项重新排列、合并：
以下是另一个代数表达式：
函数 Expand 计算乘积和幂：
Factor 执行的是 Expand 的逆运算：
输入更复杂的表达式时，将括号放在正确的位置非常重要. 因此，例如，必须以 x^(4y) 的形式给出表达式 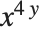. 如果省略括号，则会得到 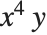. 放入太多括号永远不会有什么坏处，如果你想了解何时需要使用括号，请查看“运算符的输入形式”.
下面是一个更复杂的公式，需要几个括号：
输入表达式时，Wolfram 系统会自动应用其庞大的规则集来转换表达式. 这些规则包括标准的代数规则，例如 ，以及涉及高级数学函数的更复杂的规则.
Wolfram 系统使用标准的代数规则将 替换为 ：
Wolfram 系统不知道下面这个表达式的规则，因此保留表达式原来的形式：
转换规则的概念是一个非常笼统的概念. 实际上，可以将整个 Wolfram 系统看作只是一个将转换规则集合应用于许多不同类型的表达式的系统.
很容易陈述 Wolfram 系统遵循的一般原理. 它接受你输入的任何表达式，通过应用一系列转换规则来获取结果，在没有更多规则可以应用时停止.
■ 接受任意表达式，应用转换规则，直到结果不再发生变化.
Wolfram 系统的基本原理.
转换代数表达式
通常有许多不同的方法来表示同一个代数表达式. 举例来说，表达式 可被写为 . Wolfram 系统提供了大量函数，可在不同形式的代数表达式之间进行转换.
Expand[expr]
展开计算乘积和幂，以各项的和的形式给出结果
Factor[expr]
以最小因子的积的形式写出 expr
转换代数表达式的两个常用函数.
Expand 给出“展开形式”，将积和幂展开：
Factor 恢复原有形式：
用 Expand 很容易生成复杂的表达式：
Factor 通常给出更简单的表达式：
但是，在某些情况下，Factor 给出更复杂的表达式：
此处，Expand 给出“更简单”的形式：
化简代数表达式
在许多情况下，我们想以最简单的形式写出特定的代数表达式. 尽管很难确切地知道所有情况下“最简单的形式”是什么意思，但实际可行的是查看表达式的许多不同形式，并挑选出结构最简单的形式.
Simplify[expr]
通过应用各种标准代数变换来找到 expr 的最简单形式
FullSimplify[expr]
通过应用各种变换来找到最简单的形式
化简代数表达式.
Simplify 将 改写为因式形式：
Simplify 保留 的扩展形式，因为对于该表达式来说，因式形式更庞大：
通常可以使用 Simplify 来“清理”所得计算结果中复杂的表达式.
这里是 的积分. 可在“积分”中查看更多关于积分的讨论：
对 Integrate 的结果求导，应给出原来的表达式. 此处，得到的是更复杂版本的表达式，这种情况很常见：
Simplify 成功地给出了原来简单形式的表达式：
Simplify 被设计为在给定的表达式上尝试各种标准的代数转换. 但是，有时可能需要更复杂的转换才能找出最简单的表达式.
FullSimplify 尝试进行更大范围的转换，不仅涉及代数函数，还涉及许多其他类型的函数.
Simplify 对此表达式不执行任何操作：
FullSimplify 则将其转换为更简单的形式：
对于比较小的表达式，FullSimplify 通常会成功地将表达式明显简化. 但是对于较大的表达式，它可能变得非常慢.
原因就在于，为了完成简化，FullSimplify 必须有效地尝试将表达式的每个部分彼此组合起来，而对于大型表达式，所需要考虑的情况简直要达到天文数字.
Simplify 也要完成艰难的任务，但它被设计为避免执行 FullSimplify 尝试的一些最耗时的转换. 因此，对于简单的代数计算，我们经常会发现将 Simplify 应用于结果非常方便.
但是，在更复杂的计算中，即使是 Simplify（更不用说 FullSimplify）也可能最终需要尝试大量不同的形式，因此要花费很长时间. 在这种情况下，通常需要进行更多的受控简化，并利用对想要的形式的知识来指导化简进程.
Simplify 和 FullSimplify 使用的某些转换（例如，关于方程假设的约简）需要选择变量的顺序. 因此，化简的结果可能取决于符号的名称.
使用变量顺序 进行关于方程假设的约简，化简结果为：
如果变量顺序改为 ，则表达式没有被化简：
将表达式写成不同的形式
复杂的代数表达式通常可以被写成许多不同的形式. Wolfram 语言提供了多种将表达式从一种形式转换为另一种形式的函数.
在许多应用中，最常见的函数是 Expand、Factor 和 Simplify. 但是，如果碰到含有商数的有理表达式，则可能需要使用其他函数.
Expand[expr]
展开乘积和幂
ExpandAll[expr]
所有地方都应用 Expand
Factor[expr]
约简为因子的乘积
Together[expr]
将所有项放在公分母上
Apart[expr]
分成具有简化分母的项
Cancel[expr]
约去分子和分母的公因子
Simplify[expr]
尝试一系列代数转换，给出找到的 expr 的最简形式
转换代数表达式的函数.
这是一个可以写成许多不同形式的有理表达式：
Expand 将分子展开，但分母保留因式形式：
ExpandAll 展开所有的项，包括分母：
Together 将所有的项置于公分母上：
Apart 将表达式分成具有简单分母的单独的项：
Factor 对所有项进行因式分解，此处重新给出原来的形式：
根据 Simplify，这是原始表达式最简单的形式：
将表达式转换为所需的形式是一门艺术. 在大多数情况下，最好尝试不同的转换，直到获得所需的形式. 通常，可以利用前端中的面板来完成这项工作.
当表达式只有一个变量时，可以选择将其写为各项的和、积等. 如果表达式有多个变量，那么可能的形式就更多了. 例如，可以选择对表达式中的项进行分组，以使一个或另一个变量是“主要”变量.
Collect[expr,x]
将 x 的幂合并在一起
FactorTerms[expr,x]
提取与 x 无关的因式
重新排列含有多个变量的表达式.
这里是含有两个变量的代数表达式：
将 v 中含有 x 相同的幂的项合并在一起：
将含有 y 的幂的项合并在一起：
提取不含有 y 的项：
如上所示，即使只局限于多项式和有理表达式，任何特定表达式都可被写成许多不同的形式. 如果考虑更复杂的表达式，例如涉及高等数学函数的表达式，则可能的形式变得更加多样化. 因此，在 Wolfram 语言中内置特定函数来生成每种可能的形式是完全不可行的. 相反，Wolfram 语言允许你构建任意转换规则的组合，以便在不同形式之间进行转换. 许多 Wolfram 语言软件包都包含此类规则；“转换规则和定义”中提供了有关如何自行构建规则的详细信息
此外，还有一些其他内置 Wolfram 语言函数可用于转换表达式.
TrigExpand[expr]
将三角函数表达式展开为各项的和
TrigFactor[expr]
将三角函数表达式分解为各项的积
TrigReduce[expr]
用倍角约简三角函数表达式
TrigToExp[expr]
将三角函数转换为指数形式
ExpToTrig[expr]
将指数转换为三角函数
FunctionExpand[expr]
展开特殊函数和其他函数
ComplexExpand[expr]
假定所有变量为实数进行展开
PowerExpand[expr]
将 (xy)p 转换为 xpyp 等
其他用于转换表达式的函数.
下面展开三角函数表达式，写成所有函数都有参数 x 的形式：
这里使用三角函数恒等式生成表达式的因式形式：
用倍角约简表达式：
T假定 x 和 y 为实数，展开正弦函数：
允许 x 和 y 为复数，展开正弦函数：
无论表达式中的符号变量可能具有什么值，由 Expand 和 Factor 等函数对表达式进行的转换始终是正确的. 但是，有时，希望执行仅对符号变量某些可能的值正确的转换. PowerExpand 可执行其中一种这样的转换.
Wolfram 语言不会自动展开积的非整数次幂：
PowerExpand 可进行展开：
有假设条件的化简
Simplify[expr,assum]
有假设条件的情况下化简 expr
有假设条件的化简.
Wolfram 语言不会自动简化此函数，因为只对 x 的某些值成立：
时， 等于 ，其他情况下则非如此：
下面我们告诉 Simplify 假定 x>0，以便可以进行简化：
无法对此表达式进行自动简化：
如果假定 和 为正，则可以简化表达式：
下面是一个涉及三角函数的简单例子
Element[x,dom]
指明 x 是域 dom 中的元素
Element[{x1,x2,…},dom]
指明所有的 xi 都是域 dom 中的元素
Reals
实数
Integers
整数
Primes
质数
假设中使用的一些域.
假设 为实数，化简 ：
假设 为整数，化简正弦函数：
考虑到给定的假设，可以使用费马小定理：
这里利用了以下事实：当 为实数时， 是实数， 不是实数：
提取代数表达式的部分内容
Coefficient[expr,form]
expr 中形为 form 的项的系数
Exponent[expr,form]
expr 中形为 form 的项的最高次幂
Part[expr,n]
or
expr[[n]]
expr 中的第 n 项
用来提取多项式的部分内容的函数.
下面是一个代数表达式：
给出 e 中 x 的系数：
Exponent[expr,y] 给出在 expr 中出现的 y 的最高次幂：
给出 e 的第四项：
你可能会注意到，用于提取和的第 n 项的函数 Part[expr,n] 与“处理列表中的元素”中所述的用于提取列表中的元素的函数相同. 这不是巧合. 实际上，如“像处理列表一样处理表达式”中所讨论的那样，在结构上可以像处理列表一样处理每个 Wolfram 语言表达式. 但是，如“像处理列表一样处理表达式”中所述，要小心，因为 Wolfram 语言经常以与内部处理形式不同的形式显示代数表达式.
Coefficient 甚至适用于未显式展开的多项式：
Numerator[expr]
expr 的分子
Denominator[expr]
expr 的分母
用来提取有理表达式的部分内容的函数.
下面是一个有理表达式：
Denominator 提取出分母：
对于不是显式商数的表达式，Denominator 给出 1：
控制大型表达式的显示
在进行符号计算时，很容易得出极其复杂的表达式. 通常，甚至都不希望“看到”计算的整个结果.
如果在键入的输入后加上一个分号，则 Wolfram 语言将执行你要求的计算，但不会显示结果. 你依旧可以使用 % 或 Out[n] 来引用结果.
默认情况下，Wolfram 系统前端将在界面内以简写形式显示任何过大的输出，通过界面你可以细化输出的显示.
Wolfram 系统显示了以下计算的输出，5138 个项被省略：
显示更少和显示更多按钮可以减少或增加 Wolfram 系统显示表达式的详细程度. 显示全部按钮可去除界面，显示完整的结果，但要花费相当长的时间. 可通过设定大小限制选项设置这项功能开始起作用的阈值，点击后将打开偏好设置对话框，显示具有适当设置的面板.
抑制大型输出功能是通过使用 Wolfram 语言函数 Short 实现的. 可以直接使用 Short 来更好地控制表达式的显示. 也可以将其用于没有大到足以被默认抑制设置抑制的输出.
在键入的输入后加上一个 ;，阻止 Wolfram 语言显示复杂的计算结果：
依然可以用 % 引用结果. //Short 显示结果的单行简写形式. <<n>> 表示已省略的 n 个项：
这里显示了该表达式的三行. 现在可以看到更多部分：
给出和的项数：
command;
执行 command，但不显示结果
expr//Short
显示 expr 的单行简写形式
Short[expr,n]
显示 expr 的 n 行简写形式
一些缩短输出的方法.