ノートブックにおける入出力
| ギリシャ文字の入力 | その他の数学記号 |
| 二次元表示記号の入力 | 文章への数式の挿入 |
| 二次元式の編集と評価 | ノートブックの表示と印刷 |
| いろいろな式や記号の入力 | ハイパーリンクの設定 |
| 表と行列の作成 | 自動番号付け |
| 飾記号（添字や縦棒等） | Wolframシステムノートブックを使った解説文書の創作 |
| 英語以外の文字とキーボード | 名前付き文字 |
α をクリック | 特殊文字パレットのボタン操作 |
| \[Alpha] | 完全名を入力する |
| EscaEsc または EscalphaEsc | 標準的なエイリアスを使う（以下ではEscaEscとして表す） |
| Esc\alphaEsc | TeXエイリアスを使う |
| EscαEsc | HTMLエイリアスを使う |
Ctrl+^は，Controlキーを押しながら^キーを押す操作を示す．このキー操作を行うと，カーソルが上付き文字の位置に移動し，入力待ち状態になる．何かを入力すると，それが上付き文字として表示される．
上付き位置に移動させるCtrl+^のキー操作は，Ctrl+^が通常使われるハット(^)より直接的な入力手段ととらえると覚えやすいかもしれない．x^yとタイプしたなら，入力位置は通常の行位置のままだが，x Ctrl+^ yとタイプすると，yは直接上付き位置に挿入される．
標準的な英語キーボードにおいて，ハット記号(^)は，Shiftキーを押しながら数字6のキーを押すことで入力することができる．このキー配置のため，Wolfram言語ではCtrl+^の代替キーとしてCtrl+6が使えるようになっている．このため，ハット記号が数字6のキーのシフト位置にない英語以外のキーボードでは，Ctrl+^は機能しないだろうが，Ctrl+6は使えるはずである．
Ctrl+^ または Ctrl+6 | 上付き位置に移動 |
Ctrl+_ または Ctrl+- | 下付き位置に移動 |
Ctrl+@ または Ctrl+2 | 平方根の挿入 |
Ctrl+% または Ctrl+5 | 上付き位置から下付き位置へ移動（あるいは，その逆），または根号内部から累乗根位置へ移動（あるいは，その逆） |
Ctrl
+
/
| 分数で分母の位置に移動 |
Ctrl
+
Space
| 特別な位置から通常の行位置に戻る |
Wolfram言語では，上付き文字と下付き文字の他に，親文字の真上と真下の位置に小文字を配する，というような記述を行うこともできる．そのように記述された文字は，真上付き文字と真下付き文字と呼ばれ，総和や積の表記において，上限や下限を示すために使われる．
スクリーン表示された二次元式は，文章を編集するような感覚で編集することができる．例えば，式のある位置にカーソルを移動させ，新たな項をタイプする．または，不必要な部分を選択し，Deleteキーを押すことで，それを削除する．そして，そこに新たな項を挿入する等の編集作業を行うことができる．
Shift
+
Enter
| 現在位置のセル全体を評価する |
Shift
+
Ctrl
+
Enter
(Windows/Unix/Linux) または
Cmd
+
Return
(Mac OS X)
| |
式中で選択された項だけを評価する | |
計算を進めていくとき，普通は各ステップにおいて入力した式全体を評価させてから次のステップに進む．しかし例えば，式にある1つの式の部分だけを特定の形に変換させたいような場合は，式の構成成分ごとにいろいろな操作を行うことができる方が便利であろう．
部分的に評価を行う際は，まず，該当部分を選択し，演算子を挿入する．次に，Shift+Ctrl+Enter (Windows/Unix/Linux)またはCmd+Return (Mac OS X)を押す．
特殊記号
|
エイリアス
|
正式な形
|
シンボル
|
| x≤y | x Esc<=Esc y | x \[LessEqual] y | x <= y |
| x≥y | x Esc>=Esc y | x \[GreaterEqual] y | x >= y |
| x≠y | x Esc!=Esc y | x \[NotEqual] y | x != y |
| x∈y | x EscelEsc y | x \[Element] y | Element[x,y] |
| xy | x Esc->Esc y | x \[Rule] y | x -> y |
いくつかの演算子の特殊形式（「演算子の入力形」に完全なリストがある）
特殊記号
|
エイリアス
|
正式な形
|
シンボル
|
| x ÷ y | x EscdivEsc y | x \[Divide] y | x / y |
| x × y | x Esc*Esc y | x \[Times] y | x * y |
| x y | x EsccrossEsc y | x \[Cross] y | Cross[x,y] |
| x y | x Esc==Esc y | x \[Equal] y | x == y |
| x y | x Escl=Esc y | x \[LongEqual] y | x == y |
| x ∧ y | x Esc&&Esc y | x \[And] y | x && y |
| x ∨ y | x EscEsc y | x \[Or] y | x y |
| ¬ x | Esc!Esc x | \[Not] x | ! x |
| x y | x Esc=>Esc y | x \[Implies] y | x => y |
| x ⋃ y | x EscunEsc y | x \[Union] y | Union[x,y] |
| x ⋂ y | x EscinterEsc y | x \[Intersection] y | Intersection[x,y] |
| x y | x Esc,Esc y | x \[InvisibleComma] y | x , y |
| f x | f Esc@Esc x | f \[InvisibleApplication] x | f @ x または f[x] |
x  | x Esc+Esc  | x \[ImplicitPlus]  | x + y / z |
二次元入力
|
一次元入力
| |
 | x^y | ベキ乗 |
 | x/y | 割り算 |
 | Sqrt[x] | 平方根 |
 | x^(1/n) |  乗根 |
 | Sum[f,{i,imin,imax}] | 和 |
 | Product[f,{i,imin,imax}] | 積 |
 | Integrate[f,x] | 不定積分 |
 | Integrate[f,{x,xmin,xmax}] | 定積分 |
 | D[f,x] | 偏導関数 |
 | D[f,x,y] | 多変数偏導関数 |
 | Conjugate[x] | 複素共役 |
 | Transpose[m] | 転置 |
 | ConjugateTranspose[m] | 共役転置 |
 | Part[expr,i,j,…] | 部分抽出 |
二次元式の入力は，「二次元表示記号の入力」に記載したどの方法を使っても行うことができる．注意事項として，和や積の上限と下限は，それぞれ，真上付き文字と真下付き文字として入力する．上付き文字と下付き文字ではない．
エイリアス
|
完全名
| |
| EscsumEsc | \[Sum] | 総和記号  |
| EscprodEsc | \[Product] | 積記号  |
| EscintEsc | \[Integral] | 積分記号  |
| EscddEsc | \[DifferentialD] | 微分記号  |
| EscpdEsc | \[PartialD] | 偏微分演算子  |
| EsccoEsc | \[Conjugate] | 複素共役記号  |
| EsctrEsc | \[Transpose] | 転置記号  |
| EscctEsc | \[ConjugateTranspose] | 共役転置記号  |
| Esc[[Esc | \[LeftDoubleBracket] | 部分カッコ |
演算子の入力で使われる特殊文字（詳しくは「数学表記と他の表記法」の一覧を参照）
総和記号とギリシャ文字の大文字のシグマは全く同じように表示されるが，Wolfram言語では両者は完全に区別される．シグマは単なる文字だが，総和記号は，Wolfram言語に対してSumの演算を行うように指示をする演算子である．
総和記号とギリシャ文字の大文字のシグマが全く別なものであるように，ローマ字d，導関数を取るときに使う「partial d」の ∂，それに積分表記で使う微分記号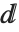 
も全く別なものである．二次元式で積分を入力するときは，必ず 
（EscddEscで入力）を使う．間違ってローマ字のdを入力してしまったなら，それはdという名前のシンボルとして扱われてしまう．積分演算子の第2構成要素としては扱ってくれない．
も全く別なものである．二次元式で積分を入力するときは，必ず 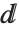（EscddEscで入力）を使う．間違ってローマ字のdを入力してしまったなら，それはdという名前のシンボルとして扱われてしまう．積分演算子の第2構成要素としては扱ってくれない．
Ctrl+, やCtrl+Enterを用いて行や列を作り上げていくことができる．特に小さい配列を作るとき等は，表・行列サブメニューの新規作成を使うより便利だろう．表・行列のメニュー項目は，主に，罫線を引く等の基本的な調整作業に適している．
Piecewise式の入力は，表入力の特殊形である．
表中の要素が複数の行や複数の列に渡るようにしたければ，要素を拡張しようとする範囲全体を選択し，メニュー項目挿入 ▶ 表・行列 ▶ 要素の結合を使う．結合されている要素の分離には挿入 ▶ 表・行列 ▶ 要素の分割を使う．
次にメニュー項目の要素の結合を使う：
Ctrl+_ または Ctrl+- | 下付き文字位置へ移動 |
Ctrl
+
Shift
+
,
| 現在位置の文字の真下へ移動 |
Ctrl+^ または Ctrl+6 | 上付き文字位置へ移動 |
Ctrl+& または Ctrl+7 | 現在位置の文字の真上へ移動 |
Ctrl
+
Space
|
通常位置へ戻る(Control
‐
Space)
|
Ctrl+^とCtrl+_が上付き文字と下付き文字に対応しているように，Ctrl+&とCtrl+4は，真上付き文字と真下付き文字に対応している．標準英語キーボードでは，Ctrl+&はCtrl+^の右隣に位置し，Ctrl+4はCtrl+_の右隣に位置する．
キー操作
|
表示
|
式
|
x Ctrl+& _ |  | OverBar[x] |
x Ctrl+& EscvecEsc |  | OverVector[x] |
x Ctrl+& ~ |  | OverTilde[x] |
x Ctrl+& ^ |  | OverHat[x] |
x Ctrl+& . |  | OverDot[x] |
x Ctrl+Shift+, _ |  | UnderBar[x] |
英語以外の言語を使い文章を書くには，アクセント符の付いた文字や，全く英語にない文字を必要とする．オペレーティングシステムの設定によっては，このような英語以外の文字をキーボードで直接入力することがシステム的にサポートされることもある．実際のシステム設定がそうなっていない場合でも，Wolfram言語を使えばこれらの文字を標準英語キーボードで一律に扱うことができる．
|
|
例えば，上付き文字の挿入で使うCtrl+6とCtrl+^は，Shift+6のキー操作で^が得られるようなキーボードではともに有効である．しかし，違ったキー配置のキーボードでは，Ctrl+6は有効だが，Ctrl+^はそうでない場合もある．
キーボードによらずパレットやメニューコマンドを使えば，常に同じ方法で上付き文字やその他の数学記号を入力することができる．また，∖記号が入力できるという前提で，入力したい記号の完全名（例えば，\[Infinity]）さえ分かっていれば，それらをタイプすることでどんなものでも入力することができる．
Wolfram言語は，今日使われる数多くの数学記号をサポートしている．ただし，提供される記号の中には，デフォルトの意味を与えられていないものもある．例えば，式x⊕yと記述すると，表示はされるが，Wolfram言語の評価上，記号
は何も意味を持たない．
は何も意味を持たない．
記号によっては，キーボードにある文字と同じように見えるが，Wolfram言語の評価では違った扱いを受けるものがある．例えば，∖[Backslash]とEsc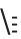
は，∖と表示されるが，キーボードで直接得られる∖とは全く別の解釈を受ける．
は，∖と表示されるが，キーボードで直接得られる∖とは全く別の解釈を受ける．
演算子の多くは，
のように，2つの被演算子の中間に置かれて機能する．しかし，演算子によっては他の位置に置かれる場合もある．例えば，山パーレンEsc
やEsc
または角カッコ∖[LeftAngleBracket]や∖[RightAngleBracket]は，作用するものの外側に置かれる．
のように，2つの被演算子の中間に置かれて機能する．しかし，演算子によっては他の位置に置かれる場合もある．例えば，山パーレンEscやEsc または角カッコ∖[LeftAngleBracket]や∖[RightAngleBracket]は，作用するものの外側に置かれる．
テキストに式を挿入するときは，メニュー項目形式変換のStandardForm（標準形）またはTraditionalForm（慣用形）を使って，選択した式をStandardFormあるいはTraditionalFormに変換できる．StandardFormは，通常，式がWolframシステムプログラムの一部であると考えられるときに適している．
ただし，表示上，数式をなるべく植字印刷的な見やすい形にするため，Wolfram言語により，例えば，演算子の両側にスペースが挿入されたりして式の形が自動調整される．このような場合，ユーザの数式の入力がWolfram言語の期待する入力法に従っていなければ，調整処理はかえって式の表示をおかしくしてしまうこともある．実際にそうなってしまったなら，植字印刷的な細かい調整を手動で行う必要が出てくるだろう．
ノートブックの使いみちによっては，文書全体の表示の仕方を変えたいときがある．フロントエンドにはスタイルだけを独立に変更できる機能が用意されているので，それを使うことで，文書を一括でスクリーン表示用または印刷用に変更することができる．書式メニューから適切なコマンドを選ぶことでこの機能が使える．
| ScreenStyleEnvironment | 表示に適したスタイル設定 |
| PrintingStyleEnvironment | 印刷に適したスタイル設定 |
| Working | スクリーン表示用の標準なスタイル定義 |
| Presentation | 発表用のスタイル定義 |
| SlideShow | 発表スライド表示のためのスタイル定義 |
| Printout | 印刷用のスタイル定義 |
選択したオブジェクトをハイパーリンクにするためのメニュー項目 | |
| Hyperlink["uri"] | ラベルとリンク先を uri と設定したハイパーリンクの出力を生成する |
| Hyperlink["label","uri"] | ラベルを label，リンク先を uri と設定したハイパーリンクの出力を生成する |
| Hyperlink[{"file.nb",None}] | 指定したノートブックへのハイパーリンクの出力を生成する |
| Hyperlink[{"file.nb","tag"}] | 指定したノートブックで tag というタグの付いたセルへのハイパーリンクの出力を生成する |
ハイパーリンクのリンク先はどのような標準Webアドレス(URI)でもよい．また，ローカルファイルシステム上のノートブックや，そのノートブック内の特定のセルにリンクすることもできる．ノートブックの特定のセルにリンクするハイパーリンクでは，セルを特定するためにセルタグを使う．指定したノートブックの中でそのセルタグが2回以上使ってある場合は，そのセルタグの付いた最初のセルに飛ぶ．
Wolfram言語コマンドのHyperlinkを使うと，出力にハイパーリンクが作成できる．そのハイパーリンクは，テキストにコピーペーストしたり，Wolfram言語で生成されている大きいインターフェースで使用することができる．
DisplayFormulaNumberedスタイルの使い方
「自動カウンタ」メニュー項目の使い方
Wolframシステムの初心者は，よくノートブックを単純な入出力行の連なりとしてとらえ，単なる計算ワークシートとして使うとか，紙の代りにスクリーンで物書きをするためのワープロとして使うことが多い．機能を生かしたノートブックの効果的な使い方は，ワークシートとワープロのどちらでもなく，実は，Wolfram言語の入出力を適切な説明文でまとめるという両者の機能をうまく併せた使い方である．文書をうまくまとめる上で最も重要な要素は，Wolfram言語の使い方であり，この言語を一貫して使うことでワークシート兼ワープロの文書を，効果的，かつ機能的なものに仕上げることができる．
ノートブックの文書例をこれまでいろいろ眺めてきて，読者は，それらが文章，数式，コンピュータコード，インタラクティブなインターフェースの4つの基本要素から構成されるものと感じられたかもしれない．しかし，Wolfram言語の重要な考え方のひとつは，数学で使われる従来の式とコンピュータコードの最高のものを誘い出す言語を提供することにある．
StandardFormで記述される Wolfram言語の式は，慣用的な数学表記法の持つまとまりと読みやすさを兼ね備えている．さらに，数学表記の式にはない式の構成上の完全な一貫性と一様性をも備えている．このため，Wolfram言語の式で問題を解き説明する限り，その問題がどの分野のものであっても，どんな記述法を使ったか等を説明する必要は全くない．なぜなら，記述されている式そのものがWolfram言語の記述であるからである．さらに，計算問題の説明をWolfram言語の式で行ったなら，ノートブックの読者にとって実際に使える文書ともなる．つまり，文書中の式を取り出しWolfram言語の入力として使うことで，読者自身で結果を確認することも可能になる．
数学表記法を長年使ってきたユーザの場合，StandardFormの式は最初は読みづらく映り，慣れるまでに多少時間がかかるだろう．実際，使いはじめの段階では，記述しづらい式でもわざわざ隠しタグを付けたりして，できる限りTraditionalFormを使おうとする傾向が多くのユーザに見受けられる．しかし，慣れてくると，StandardFormとTraditionalFormを併せて使うようになり，大概の用途ではStandardFormが最も効果的で分かりやすい提示手段であることが分かってくるようになる．
普通，数学の解説では，長蛇の文章の代りに短い式を使い手短に話を進めていく．ノートブックでもStandardFormを使い同様なアプローチを取ることができる．また，そうすることで，式を，計算をするだけの単なる数式ではなくプログラミング，アルゴリズム，グラフィックス，インターフェースをも表すものとして使えるので，曖昧になりがちな説明をさらにコンパクトに，また，より正確なものにできる．
文字の解釈
MakeExpressionで独自の規則を与えることにより，解釈を一時的に変更することが可能である．
文字および文字に準ずるフォーム | シンボル名で使用 |
中置形演算子 | 例：  |
前置形演算子 | 例：  |
後置形演算子 | 例：  |
両側演算子 | 例：  |
複合演算子 | 例：  |
原始演算子 | 通常のキーボードからタイプできる演算記号文字 |
スペース文字 | 通常のスペースと同様に解釈される |
構造要素 | 構造の指定に使用される文字（通常は解釈では無視される） |
解釈不可能要素 | 欠落している情報があることを示す文字 |
演算子の優先順位は「演算子の入力形」に示されている．
命名の約束
スタイル | Script，Gothic等 |
変形 | Curly，Gray等 |
大文字・小文字 | Capital等 |
変更子 | |
方向 | |
基 | |
添付符号 | Acute，Ring等 |
エイリアス
Wolfram言語はシステム自体でのエイリアス(alias)，およびTeX，SGML，HTMLで使われる文字に基づいたエイリアスをサポートしている．名前に矛盾がない限り，plain TeX，LaTeXおよびAMSTeXに対応する文字名はすべてサポートされている．TeX，SGML，HTMLで使用されるエイリアスは，以下の文字一覧には明示的に示されていないことに注意してほしい．
- 標準キーボードで演算子の代替となる文字は，その演算をエイリアスとして使用する（例：
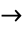にはEsc->Esc，
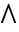にはEsc&&Esc）． - 単一文字からなるエイリアスはほとんどの場合ギリシャ文字である．
- 大文字のエイリアスはやはり大文字で始まる．
- エイリアスの命名法で曖昧さがある場合は，一般性のより少ない方の文字に対応するエイリアスの先頭にスペースが挿入される（例：\[Rule]にはEsc->Esc，\[RightArrow]にはEsc␣->Esc）．
- !はNot文字の代りに先頭に挿入される．
- TeXのエイリアスはバックスラッシュ∖で始まる．
- SGMLのエイリアスはアンドサイン&で始まる．
- ユーザ定義のエイリアスは伝統的にドットまたはコンマで始まる．
フォントの一致
テキストを特定のフォントで印刷する場合，Wolframシステムノートブックのフロントエンドは，そのフォント内で利用可能なすべての文字を使用する．Wolframシステム特殊フォントはそれ以外の文字だけに使用される．