Modularity and the Naming of Things
The Wolfram Language normally assumes that all your variables are global. This means that every time you use a name like x, the Wolfram Language normally assumes that you are referring to the same object.
Particularly when you write programs, however, you may not want all your variables to be global. You may, for example, want to use the name x to refer to two quite different variables in two different programs. In this case, you need the x in each program to be treated as a local variable.
You can set up local variables in the Wolfram Language using modules. Within each module, you can give a list of variables which are to be treated as local to the module.
| Module[{x,y,…},body] | a module with local variables x, y, … |
The most common way that modules are used is to set up temporary or intermediate variables inside functions you define. It is important to make sure that such variables are kept local. If they are not, then you will run into trouble whenever their names happen to coincide with the names of other variables.
You can treat local variables in modules just like other symbols. Thus, for example, you can use them as names for local functions, you can assign attributes to them, and so on.
When you set up a local variable in a module, the Wolfram Language initially assigns no value to the variable. This means that you can use the variable in a purely symbolic way, even if there was a global value defined for the variable outside the module.
Here Length simply receives a number as its argument:
The local variable t has no value, so it acts as a symbol, and Expand produces the anticipated algebraic result:
| Module[{x=x0,y=y0,…},body] | a module with initial values for local variables |
You can define initial values for any of the local variables in a module. The initial values are always evaluated before the module is executed. As a result, even if a variable x is defined as local to the module, the global x will be used if it appears in an expression for an initial value.
| lhs:=Module[vars,rhs/;cond] | share local variables between rhs and cond |
When you set up /; conditions for definitions, you often need to introduce temporary variables. In many cases, you may want to share these temporary variables with the body of the right‐hand side of the definition. The Wolfram Language allows you to enclose the whole right‐hand side of your definition in a module, including the condition.
The Wolfram Language shares the value of the local variable t between the condition and the body of the right‐hand side:
| With[{x=x0,y=y0,…},body] | define local constants x, y, … |
Module allows you to set up local variables, to which you can assign values and then change them. Often, however, all you really need are local constants, to which you assign a value only once. The Wolfram Language With construct allows you to set up such local constants.
The way With[{x=x0,…},body] works is to take body, and replace every occurrence of x, etc. in it by x0, etc. You can think of With as a generalization of the /. operator, suitable for application to Wolfram Language code instead of other expressions.
In some respects, With is like a special case of Module, in which each local variable is assigned a value exactly once.
One of the main reasons for using With rather than Module is that it typically makes the Wolfram Language programs you write easier to understand. In a module, if you see a local variable x at a particular point, you potentially have to trace through all of the code in the module to work out the value of x at that point. In a With construct, however, you can always find out the value of a local constant simply by looking at the initial list of values, without having to trace through specific code.
If you have several With constructs, it is always the innermost one for a particular variable that is in effect. You can mix Module and With. The general rule is that the innermost one for a particular variable is the one that is in effect.
With nested With constructs, the innermost one is always the one in effect:
Except for the question of when x and body are evaluated, With[{x=x0,…},body] works essentially like body/.x->x0. However, With behaves in a special way when the expression body itself contains With or Module constructs. The main issue is to prevent the local constants in the various With constructs from conflicting with each other, or with global objects. The details of how this is done are discussed in "How Modules Work".
The way modules work in the Wolfram Language is basically very simple. Every time any module is used, a new symbol is created to represent each of its local variables. The new symbol is given a unique name which cannot conflict with any other names. The name is formed by taking the name you specify for the local variable, followed by $, with a unique "serial number" appended.
The serial number is found from the value of the global variable $ModuleNumber. This variable counts the total number of times any Module of any form has been used.
Module generates symbols with names of the form x$nnn to represent each local variable. |
For most purposes, you will never have to deal directly with the actual symbols generated inside modules. However, if for example you start up a dialog while a module is being executed, then you will see these symbols. The same is true whenever you use functions like Trace to watch the evaluation of modules.
You see the symbols that are generated inside modules when you use Trace:
Under some circumstances, it is convenient explicitly to return symbols that are generated inside modules.
| Unique[x] | generate a new symbol with a unique name of the form x$nnn |
| Unique[{x,y,…}] | generate a list of new symbols |
The function Unique allows you to generate new symbols in the same way as Module does. Each time you call Unique, $ModuleNumber is incremented, so that the names of new symbols are guaranteed to be unique.
Each time you call Unique, you get a symbol with a larger serial number:
If you call Unique with a list of names, you get the same serial number for each of the symbols:
You can use the standard Wolfram Language ?name mechanism to get information on symbols that were generated inside modules or by the function Unique.
Symbols generated by Module behave in exactly the same way as other symbols for the purposes of evaluation. However, these symbols carry the attribute Temporary, which specifies that they should be removed completely from the system when they are no longer used. Thus most symbols that are generated inside modules are removed when the execution of those modules is finished. The symbols survive only if they are explicitly returned.
The new variable is removed when the execution of the module is finished, so it does not show up here:
You should realize that the use of names such as x$nnn for generated symbols is purely a convention. You can in principle give any symbol a name of this form. But if you do, the symbol may collide with one that is produced by Module.
An important point to note is that symbols generated by Module are in general unique only within a particular Wolfram Language session. The variable $ModuleNumber which determines the serial numbers for these symbols is always reset at the beginning of each session.
This means in particular that if you save expressions containing generated symbols in a file, and then read them into another session, there is no guarantee that conflicts will not occur. This is unlikely in practice, as generated symbols are generally temporary. A possible way to deal with conflicts is to manually set $ModuleNumber to a large value, for example 2^($SystemWordLength-8), at the start of a session where a file with temporary symbols will be read in.
Having generated appropriate symbols to represent the local variables you have specified, Module[vars,body] then has to evaluate body using these symbols. The first step is to take the actual expression body as it appears inside the module, and effectively to use With to replace all occurrences of each local variable name with the appropriate generated symbol. After this is done, Module actually performs the evaluation of the resulting expression.
An important point to note is that Module[vars,body] inserts generated symbols only into the actual expression body. It does not, for example, insert such symbols into code that is called from body, but does not explicitly appear in body.
"Blocks and Local Values" discusses how you can use Block to set up "local values" which work in a different way.
Most of the time, you will probably set up modules by giving explicit Wolfram Language input of the form Module[vars,body]. Since the function Module has the attribute HoldAll, the form of body will usually be kept unevaluated until the module is executed.
It is, however, possible to build modules dynamically in the Wolfram Language. The generation of new symbols, and their insertion into body are always done only when a module is actually executed, not when the module is first given as Wolfram Language input.
Module and With allow you to give a specific list of symbols whose names you want to treat as local. In some situations, however, you want to automatically treat certain symbol names as local.
For example, if you use a pure function such as Function[{x},x+a], you want x to be treated as a "formal parameter", whose specific name is local. The same is true of the x that appears in a rule like f[x_]->x^2, or a definition like f[x_]:=x^2.
The Wolfram Language uses a uniform scheme to make sure that the names of formal parameters that appear in constructs like pure functions and rules are kept local, and are never confused with global names. The basic idea is to replace formal parameters when necessary by symbols with names of the form x$. By convention, x$ is never used as a global name.
The Wolfram Language renames the formal parameter y in the inner function to avoid conflict with the global object y:
In general, the Wolfram Language renames the formal parameters in an object like Function[vars,body] whenever body is modified in any way by the action of another pure function.
The Wolfram Language renames formal parameters in pure functions more liberally than is strictly necessary. In principle, renaming could be avoided if the names of the formal parameters in a particular function do not actually conflict with parts of expressions substituted into the body of the pure function. For uniformity, however, the Wolfram Language still renames formal parameters even in such cases.
In this case, the formal parameter x in the inner function shields the body of the function, so no renaming is needed:
As mentioned in "Pure Functions", pure functions in the Wolfram Language are like 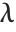 expressions in formal logic. The renaming of formal parameters allows Wolfram Language pure functions to reproduce all the semantics of standard
expressions in formal logic. The renaming of formal parameters allows Wolfram Language pure functions to reproduce all the semantics of standard 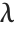 expressions faithfully.
expressions faithfully.
| Function[{x,…},body] | local parameters |
| lhs->rhs and lhs:>rhs | local pattern names |
| lhs=rhs and lhs:=rhs | local pattern names |
| With[{x=x0,…},body] | local constants |
| Module[{x,…},body] | local variables |
The Wolfram Language has several "scoping constructs" in which certain names are treated as local. When you mix these constructs in any way, the Wolfram Language does appropriate renamings to avoid conflicts.
Here the local constant in the inner With is renamed to avoid a conflict:
The Wolfram Language treats transformation rules as scoping constructs, in which the names you give to patterns are local. You can set up named patterns either using x_, x__, and so on, or using x:patt.
In a rule like f[x_]->x+y, the x that appears on the right‐hand side goes with the name of the x_ pattern. As a result, this x is treated as a variable local to the rule, and cannot be modified by other scoping constructs.
The y, on the other hand, is not local to the rule, and can be modified by other scoping constructs. When this happens, the Wolfram Language renames the patterns in the rule to prevent the possibility of a conflict.
When you use With on a scoping construct, the Wolfram Language automatically performs appropriate renamings. In some cases, however, you may want to make substitutions inside scoping constructs, without any renaming. You can do this using the /. operator.
When you apply a rule such as f[x_]->rhs, or use a definition such as f[x_]:=rhs, the Wolfram Language implicitly has to substitute for x everywhere in the expression rhs. It effectively does this using the /. operator. As a result, such substitution does not respect scoping constructs. However, when the insides of a scoping construct are modified by the substitution, the other variables in the scoping construct are renamed.
When you set up mathematical formulas, you often have to introduce various kinds of local objects or "dummy variables". You can treat such dummy variables using modules and other Wolfram Language scoping constructs.
Integration variables are a common example of dummy variables in mathematics. When you write down a formal integral, conventional notation requires you to introduce an integration variable with a definite name. This variable is essentially "local" to the integral, and its name, while arbitrary, must not conflict with any other names in your mathematical expression.
Since you have used a module, the Wolfram Language automatically renames the integration variable to avoid a conflict:
In many cases, the most important issue is that dummy variables should be kept local, and should not interfere with other variables in your mathematical expression. In some cases, however, what is instead important is that different uses of the same dummy variable should not conflict.
Repeated dummy variables often appear in products of vectors and tensors. With the "summation convention", any vector or tensor index that appears exactly twice is summed over all its possible values. The actual name of the repeated index never matters, but if there are two separate repeated indices, it is essential that their names do not conflict.
There are many situations in mathematics where you need to have variables with unique names. One example is in representing solutions to equations. With an equation like 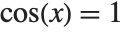 , there are an infinite number of solutions, each of the form
, there are an infinite number of solutions, each of the form 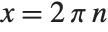 , where
, where 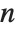 is a dummy variable that can be equal to any integer.
is a dummy variable that can be equal to any integer.
Another place where unique objects are needed is in representing "constants of integration". When you do an integral, you are effectively solving an equation for a derivative. In general, there are many possible solutions to the equation, differing by additive "constants of integration". The standard Wolfram Language Integrate function always returns a solution with no constant of integration. But if you were to introduce constants of integration, you would need to use modules to make sure that they are always unique.
Modules in the Wolfram Language allow you to treat the names of variables as local. Sometimes, however, you want the names to be global, but values to be local. You can do this in the Wolfram Language using Block.
| Block[{x,y,…},body] | evaluate body using local values for x,y,… |
| Block[{x=x0,y=y0,…},body] | assign initial values to x,y,… |
As described in "Modules and Local Variables", the variable x in a module such as Module[{x},body] is always set up to refer to a unique symbol, different each time the module is used, and distinct from the global symbol x. The x in a block such as Block[{x},body] is, however, taken to be the global symbol x. What the block does is to make the value of x local. The value x had when you entered the block is always restored when you exit the block. And during the execution of the block, x can take on any value.
Blocks in the Wolfram Language effectively allow you to set up "environments" in which you can temporarily change the values of variables. Expressions you evaluate at any point during the execution of a block will use the values currently defined for variables in the block. This is true whether the expressions appear directly as part of the body of the block, or are produced at any point in its evaluation.
An important implicit use of Block in the Wolfram Language is for iteration constructs such as Do, Sum, and Table. The Wolfram Language effectively uses Block to set up local values for the iteration variables in all of these constructs.
The local values in iteration constructs are slightly more general than in Block. They handle variables such as a[1], as well as pure symbols:
When you set up functions in the Wolfram Language, it is sometimes convenient to have "global variables" that can affect the functions without being given explicitly as arguments. Thus, for example, the Wolfram Language itself has a global variable $RecursionLimit that affects the evaluation of all functions, but is never explicitly given as an argument.
The Wolfram Language will usually keep any value you define for a global variable until you explicitly change it. Often, however, you want to set up values that last only for the duration of a particular computation, or part of a computation. You can do this by making the values local to a Wolfram Language block.
You can use global variables not only to set parameters in functions, but also to accumulate results from functions. By setting up such variables to be local to a block, you can arrange to accumulate results only from functions called during the execution of the block.
When you enter a block such as Block[{x},body], any value for x is removed. This means that you can in principle treat x as a "symbolic variable" inside the block. However, if you explicitly return x from the block, it will be replaced by its value outside the block as soon as it is evaluated.
When you write a program in the Wolfram Language, you should always try to set it up so that its parts are as independent as possible. In this way, the program will be easier for you to understand, maintain, and add to.
One of the main ways to ensure that different parts of a program do not interfere is to give their variables only a certain "scope". The Wolfram Language provides two basic mechanisms for limiting the scope of variables: modules and blocks.
In writing actual programs, modules are far more common than blocks. When scoping is needed in interactive calculations, however, blocks are often convenient.
Most traditional computer languages use a so‐called "lexical scoping" mechanism for variables, which is analogous to the module mechanism in the Wolfram Language. Some symbolic computer languages such as LISP also allow "dynamic scoping", analogous to Wolfram Language blocks.
When lexical scoping is used, variables are treated as local to a particular section of the code in a program. In dynamic scoping, the values of variables are local to a part of the execution history of the program.
In compiled languages like C and Java, there is a very clear distinction between "code" and "execution history". The symbolic nature of the Wolfram Language makes this distinction slightly less clear, since "code" can in principle be built up dynamically during the execution of a program.
What Module[vars,body] does is to treat the form of the expression body at the time when the module is executed as the "code" of a Wolfram Language program. It examines the expression, and when any of the vars explicitly appears in this "code", it is considered to be local. Normal evaluation then proceeds.
Block[vars,body] does not look at the form of the expression body. Instead, it records the current value of each of the vars. Throughout the evaluation of body, the block uses local values for the vars, and then restores their original values once the evaluation of body is finished.
It is always a good idea to give variables and functions names that are as explicit as possible. Sometimes, however, such names may get inconveniently long.
In the Wolfram Language, you can use the notion of "contexts" to organize the names of symbols. Contexts are particularly important in Wolfram Language packages that introduce symbols whose names must not conflict with those of any other symbols. If you write Wolfram Language packages, or make sophisticated use of packages that others have written, then you will need to know about contexts.
The basic idea is that the full name of any symbol is broken into two parts: a context and a short name. The full name is written as context`short, where the ` is the backquote or grave accent character (ASCII decimal code 96), called a "context mark" in the Wolfram Language.
It is typical to have all the symbols that relate to a particular topic in a particular context. Thus, for example, symbols that represent physical units might have a context PhysicalUnits`. Such symbols might have full names like PhysicalUnits`Joule or PhysicalUnits`Mole.
Although you can always refer to a symbol by its full name, it is often convenient to use a shorter name.
At any given point in a Wolfram Language session, there is always a current context $Context. You can refer to symbols that are in this context simply by giving their short names, unless the symbol is shadowed by the symbol with the same short name on the $ContextPath. If a symbol with the given short name exists on the context path, it will be used instead of the symbol in the current context.
No symbols with the name x exist on $ContextPath, so the short name is sufficient to refer to the symbol in the current context:
Contexts in the Wolfram Language work somewhat like file directories in many operating systems. You can always specify a particular file by giving its complete name, including its directory. But at any given point, there is usually a current working directory, analogous to the current Wolfram Language context. Files that are in this directory can then be specified just by giving their short names.
Like directories in many operating systems, contexts in the Wolfram Language can be hierarchical. Thus, for example, the full name of a symbol can involve a sequence of context names, as in c1`c2`c3`name.
| context `name or c1`c2 … `name | a symbol in an explicitly specified context |
| `name | a symbol in the current context |
| `context`name or `c1`c2` … `name | a symbol in a specific context relative to the current context |
| name |
a symbol in the current context, or found on the context search path
|
When you start a Wolfram Language session, the default current context is Global`. Symbols that you introduce will usually be in this context. However, built‐in symbols such as Pi are in the context System`.
In order to let you easily access not only symbols in the context Global`, but also in contexts such as System`, the Wolfram Language supports the notion of a context search path. At any point in a Wolfram Language session, there is both a current context $Context, and also a current context search path $ContextPath. The idea of the search path is to allow you to type in the short name of a symbol, then have the Wolfram Language search in a sequence of contexts to find a symbol with that short name.
The context search path for symbols in the Wolfram Language is analogous to the "search path" for program files provided in operating systems. Since $Context is searched after $ContextPath, you can think of it as having "." appended to the file search path.
| Context[s] | the context of a symbol |
| $Context | the current context in a Wolfram Language session |
| $ContextPath | the current context search path |
| $ContextAliases | a list of aliases for contexts |
| Contexts[] | a list of all contexts |
When you use contexts in the Wolfram Language, there is no reason that two symbols that are in different contexts cannot have the same short name. Thus, for example, you can have symbols with the short name Mole both in the context PhysicalUnits` and in the context BiologicalOrganisms`.
There is, however, then the question of which symbol you actually get when you type in only the short name Mole. The answer to this question is determined by which of the contexts comes first in the sequence of contexts listed in the context search path.
This adds two additional contexts to $ContextPath. Typically, the Wolfram Language adds new contexts to the beginning of $ContextPath:
In general, when you type in a short name for a symbol, the Wolfram Language assumes that you want the symbol with that name whose context appears earliest in the context search path. As a result, symbols with the same short name whose contexts appear later in the context search path or symbols with the same short name in the current context are effectively "shadowed". To refer to these symbols, you need to use their full names.
The Wolfram Language issues a message when you introduce new symbols that "shadow" existing symbols with your current choice for $ContextPath. In addition, in the notebook front end the Wolfram Language warns you of shadowed symbols by coloring them red.
This introduces a symbol with short name Mole in the context Global`:The Wolfram Language warns you that the new symbol shadows existing symbols with short name Mole:
Now when you type in Mole, you get the symbol that appears first in the context path, PhysicalUnits`:
If you once introduce a symbol that shadows existing symbols, it will continue to do so until you either rearrange $ContextPath, or explicitly remove the symbol. You should realize that it is not sufficient to clear the value of the symbol; you need to actually remove the symbol completely from the Wolfram Language. You can do this using the function Remove[s].
When the Wolfram Language prints out the name of a symbol, it has to choose whether to give the full name, or just the short name. What it does is to give whatever version of the name you would have to type in to get the particular symbol, given your current settings for $Context and $ContextPath.
If you type in a short name for which there is no symbol either in the current context, or in any context on the context search path, then the Wolfram Language has to create a new symbol with this name. It always puts new symbols of this kind in the current context, as specified by $Context.
A typical package written in the Wolfram Language introduces several new symbols intended for use outside the package. These symbols may correspond for example to new functions or new objects defined in the package.
There is a general convention that all new symbols introduced in a particular package are put into a context whose name is related to the name of the package. When you read in the package, it adds this context at the beginning of your context search path $ContextPath.
The package prepends its context to $ContextPath:
The full names of symbols defined in packages are often quite long. In most cases, however, you will only need to use their short names. The reason for this is that after you have read in a package, its context is added to $ContextPath, so the context is automatically searched whenever you type in a short name.
There is a complication, however, when two symbols with the same short name appear in two different packages. In such a case, the Wolfram Language will warn you when you read in the second package. It will tell you which symbols will be "shadowed" by the new symbols that are being introduced.
The symbol ProvablePrimeQ in the context PrimalityProving` is shadowed by the symbol with the same short name in the new package:
Conflicts can occur not only between symbols in different packages, but also between symbols in packages and symbols that you introduce directly in your Wolfram Language session. If you define a symbol in your current context, then this symbol may become shadowed by another symbol with the same short name in packages that you read in. The reason for this is that the Wolfram Language searches for symbols in contexts on the context search path before looking in the current context.
The ScalarQ from the package is used:
If you get into the situation where unwanted symbols are shadowing the symbols you want, the best thing to do is usually to get rid of the unwanted symbols using Remove[s]. An alternative that is sometimes appropriate is to rearrange the entries in $ContextPath and to reset the value of $Context so as to make the contexts that contain the symbols you want be the ones that are searched first.
| $Packages | a list of the contexts corresponding to all packages loaded into your Wolfram Language session |
One of the most important features of the Wolfram Language is that it is an extensible system. There is a certain amount of mathematical and other functionality that is built into the Wolfram Language. But by using the Wolfram Language, it is always possible to add more functionality.
For many kinds of calculations, what is built into the standard version of the Wolfram Language will be quite sufficient. However, if you work in a particular specialized area, you may find that you often need to use certain functions that are not built into the Wolfram Language.
In such cases, you may well be able to find a Wolfram Language package that contains the functions you need. Wolfram Language packages are files written in the Wolfram Language. They consist of collections of Wolfram Language definitions which "teach" the Wolfram Language about particular application areas.
If you want to use functions from a particular package, you must first read the package into the Wolfram Language. The details of how to do this are discussed in "External Programs". There are various conventions that govern the names you should use to refer to packages.
The ProvablePrimeQ function is defined in the package:
There are a number of subtleties associated with such issues as conflicts between names of functions in different packages. These are discussed in "Contexts and Packages". One point to note, however, is that you should not refer to a function that you will read from a package before actually reading in the package. If you do this by mistake, the Wolfram Language will issue a message warning about the duplicate names and use the one last defined. This means that your version of the function will not be used; it will be the one from the package. You can execute the command Remove["name"] to get rid of the package function.
| Remove["name"] | remove a function that has been introduced in error |
The fact that the Wolfram Language can be extended using packages means that the boundary of exactly what is "part of the Wolfram Language" is quite blurred. As far as usage is concerned, there is actually no difference between functions defined in packages and functions that are fundamentally built into the Wolfram Language.
In fact, a fair number of the functions built into the core Wolfram Language are actually implemented as Wolfram Language packages. However, for most Wolfram System installations, the necessary packages have been preloaded, so that the functions they define are always present.
To blur the boundary of what is part of the Wolfram Language even further, "Automatic Loading of Packages" describes how you can tell the Wolfram Language automatically to load a particular package if you ever try to use a certain function. If you never use that function, then it will not be present. But as soon as you try to use it, its definition will be read in from a Wolfram Language package.
As a practical matter, the functions that should be considered "part of the Wolfram Language" are probably those that are present in all Wolfram System installations. It is these functions that are primarily discussed in this documentation.
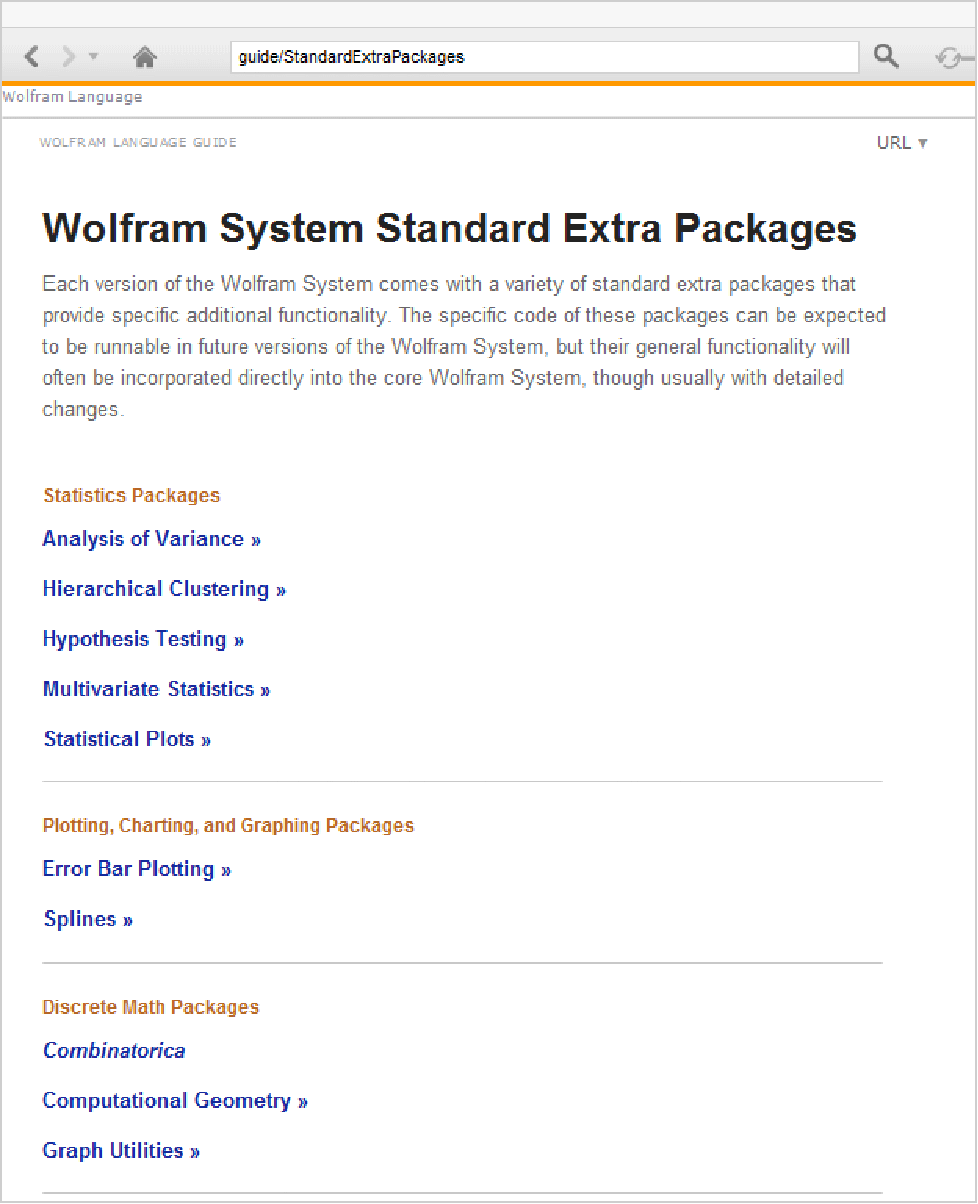
Nevertheless, most versions of the Wolfram System come with a standard set of Wolfram Language packages, which contain definitions for many more functions. To use these functions, you must usually read in the necessary packages explicitly.
You can use the Documentation Center to get information on Wolfram Language Standard Extra Packages.
It is possible to set your Wolfram System up so that particular packages are preloaded, or are automatically loaded when needed. If you do this, then there may be many functions that appear as standard in your version of the Wolfram System, but which are not documented in the Wolfram Language reference pages.
One point that should be mentioned is the relationship between packages and notebooks. Both are stored as files on your computer system, and both can be read into the Wolfram System. However, a notebook is intended to be displayed, typically with a notebook interface, while a package is intended only to be used as Wolfram Language input. Many notebooks in fact contain sections that can be considered as packages, and which contain sequences of definitions intended for input to the Wolfram Language. There are also capabilities that allow packages set up to correspond to notebooks to be maintained automatically.
In a typical Wolfram Language package, there are generally two kinds of new symbols that are introduced. The first kind are ones that you want to “export” for use outside the package. The second kind are ones that you want to use only internally within the package. You can distinguish these two kinds of symbols by putting them in different contexts.
The usual convention is to put symbols intended for export in a context with a name Package` that corresponds to the name of the package. Whenever the package is read in, it adds this context to the context search path, so that the symbols in this context can be referred to by their short names.
Symbols that are not intended for export, but are instead intended only for internal use within the package, are conventionally put into a context with the name Package`Private`. This context is not added to the context search path. As a result, the symbols in this context cannot be accessed except by giving their full names.
| Package` | symbols for export |
| Package`Private` | symbols for internal use only |
| System` | built‐in Wolfram Language symbols |
| Needed1`
,
Needed2`
,
…
| other contexts needed in the package |
There is a standard sequence of Wolfram Language commands that is typically used to set up the contexts in a package. These commands set the values of $Context and $ContextPath so that the new symbols which are introduced are created in the appropriate contexts.
| BeginPackage["Package`"] | set Package` to be the current context, and put only System` on the context search path |
| f::usage="text"
,
…
|
introduce the objects intended for export (and no others)
|
| Begin["`Private`"] | set the current context to Package`Private` |
| f[args]=value
,
…
| give the main body of definitions in the package |
| End[] |
revert to the previous context (here
Package`
)
|
| EndPackage[] | end the package, prepending the Package` to the context search path |
BeginPackage["Collatz`"]
Collatz::usage =
"Collatz[n] gives a list of the iterates in the 3n+1 problem,
starting from n. The conjecture is that this sequence always
terminates."
Begin["`Private`"]
Collatz[1] := {1}
Collatz[n_Integer] := Prepend[Collatz[3 n + 1], n] /; OddQ[n] && n > 0
Collatz[n_Integer] := Prepend[Collatz[n/2], n] /; EvenQ[n] && n > 0
End[ ]
EndPackage[ ]
Defining usage messages at the beginning of a package is the standard way of making sure that symbols you want to export are created in the appropriate context. The way this works is that in defining these messages, the only symbols you mention are exactly the ones you want to export. These symbols are then created in the context Package`, which is then current.
In the actual definitions of the functions in a package, there are typically many new symbols, introduced as parameters, temporary variables, and so on. The convention is to put all these symbols in the context Package`Private`, which is not put on the context search path when the package is read in.
The EndPackage command in the package adds the context associated with the package to the context search path:
In the Collatz package, the functions that are defined depend only on built‐in Wolfram Language functions. Often, however, the functions defined in one package may depend on functions defined in another package.
Two things are needed to make this work. First, the other package must be read in, so that the functions needed are defined. And second, the context search path must include the context that these functions are in.
You can explicitly tell the Wolfram Language to read in a package at any point using the command <<context`. ("Files for Packages" discusses the tricky issue of translation from system‐independent context names to system‐dependent file names.) Often, however, you want to set it up so that a particular package is read in only if it is needed. The command Needs["context`"] tells the Wolfram Language to read in a package if the context associated with that package is not already in the list $Packages.
| Get["context`"] or <<context` | read in the package corresponding to the specified context |
| Needs["context`"] | read in the package if the specified context is not already in $Packages |
| BeginPackage["Package`",{"Needed1`", … }] | |
begin a package, specifying that certain contexts in addition to System` are needed | |
If you use BeginPackage["Package`"] with a single argument, the Wolfram Language puts on the context search path only the Package` context and the contexts for built‐in Wolfram Language symbols. If the definitions you give in your package involve functions from other packages, you must make sure that the contexts for these packages are also included in your context search path. You can do this by giving a list of the additional contexts as a second argument to BeginPackage. BeginPackage automatically calls Needs on these contexts, reading in the corresponding packages if necessary, and then making sure that the contexts are on the context search path.
Executing a function like Begin which manipulates contexts changes the way that the Wolfram Language interprets names you type in. However, you should realize that the change is effective only in subsequent expressions that you type in. The point is that the Wolfram Language always reads in a complete input expression, and interprets the names in it, before it executes any part of the expression. As a result, by the time Begin is executed in a particular expression, the names in the expression have already been interpreted, and it is too late for Begin to have an effect.
The fact that context manipulation functions do not have an effect until the next complete expression is read in means that you must be sure to give those functions as separate expressions, typically on separate lines, when you write Wolfram Language packages.
Context manipulation functions are used primarily as part of packages intended to be read into the Wolfram Language. Sometimes, however, you may find it convenient to use such functions interactively.
This can happen, for example, if you go into a dialog, say using TraceDialog, while executing a function defined in a package. The parameters and temporary variables in the function are typically in a private context associated with the package. Since this context is not on your context search path, the Wolfram Language will print out the full names of the symbols, and will require you to type in these full names in order to refer to the symbols. You can however use Begin["Package`Private`"] to make the private context of the package your current context. This will make the Wolfram Language print out short names for the symbols, and allow you to refer to the symbols by their short names.
When you create or use Wolfram Language packages, you will often want to refer to files in a system‐independent way. You can use contexts to do this.
The basic idea is that on every computer system there is a convention about how files corresponding to Wolfram Language contexts should be named. Then, when you refer to a file using a context, the particular version of the Wolfram Language you are using converts the context name to the file name appropriate for the computer system you are on.
| name.mx | file in DumpSave format |
| name.mx/$SystemID/name.mx | file in DumpSave format for your computer system |
| name.m | file in Wolfram Language source format |
| name/init.m | initialization file for a particular directory |
| dir/… | files in other directories specified by $Path |
The Wolfram Language is set up so that <<name` will automatically try to load the appropriate version of a file. It will first try to load a name.mx file that is optimized for your particular computer system. If it finds no such file, then it will try to load a name.m file containing ordinary system‐independent Wolfram Language input.
If name is a directory, then the Wolfram Language will try to load the initialization file init.m in that directory. The purpose of the init.m file is to provide a convenient way to set up Wolfram Language packages that involve many separate files. The idea is to allow you to give just the command <<name`, but then to load init.m to initialize the whole package, reading in whatever other files are necessary.
Other tutorials have discussed explicit loading of Wolfram Language packages using <<package and Needs[package]. Sometimes, however, you may want to set the Wolfram Language up so that it automatically loads a particular package when the package is needed.
You can use DeclarePackage to give the names of symbols which are defined in a particular package. Then, when one of these symbols is actually used, the Wolfram Language will automatically load the package where the symbol is defined.
| DeclarePackage["context`",{"name1","name2",…}] | |
declare that a package should automatically be loaded if a symbol with any of the names namei is used | |
This specifies that the symbols VariationalD, EulerEquations, and FirstIntegral are defined in VariationalMethods`:
When you first use VariationalD, the Wolfram Language automatically loads the package that defines it:
When you set up a large collection of Wolfram Language packages, it is often a good idea to create an additional “names file” which contains a sequence of DeclarePackage commands, specifying packages to load when particular names are used. Within a particular Wolfram System session, you then need to load explicitly only the names file. When you have done this, all the other packages will automatically be loaded if and when they are needed.
DeclarePackage works by immediately creating symbols with the names you specify, but giving each of these symbols the special attribute Stub. Whenever the Wolfram Language finds a symbol with the Stub attribute, it automatically loads the package corresponding to the context of the symbol, in an attempt to find the definition of the symbol.
| Symbol["name"] | construct a symbol with a given name |
| SymbolName[symb] | find the name of a symbol |
Once you have made an assignment such as x=2, then whenever x is evaluated, it is replaced by 2. Sometimes, however, you may want to continue to refer to x itself, without immediately getting the value of x.
You can do this by referring to x by name. The name of the symbol x is the string "x", and even though x itself may be replaced by a value, the string "x" will always stay the same.
| NameQ["form"] | test whether any symbol has a name which matches form |
| Names["form"] | give a list of all symbol names which match form |
| Contexts["form`"] | give a list of all context names which match form |
You can specify the form of symbol names using string patterns of the kind discussed in "String Patterns". "x*" stands, for example, for all names that start with x.
| Clear["form"] | clear the values of all symbols whose names match form |
| Clear["context`*"] | clear the values of all symbols in the specified context |
| Remove["form"] | remove completely all symbols whose names match form |
| Remove["context`*"] | remove completely all symbols in the specified context |
| Remove["Global`*"] | remove completely all symbols in the Global` context |
If you do not set up any additional contexts, then all the symbols that you introduce in a Wolfram Language session will be placed in the Global` context. You can remove these symbols completely using Remove["Global`*"]. Built‐in Wolfram Language objects are in the System` context, and are thus unaffected by this.
The Wolfram Language creates a new symbol when you first enter a particular name. Sometimes it is useful to "intercept" the process of creating a new symbol. The Wolfram Language provides several ways to do this.
| On[General::newsym] | print a message whenever a new symbol is created |
| Off[General::newsym] | switch off the message printed when new symbols are created |
Generating a message when the Wolfram Language creates a new symbol is often a good way to catch typing mistakes. The Wolfram Language itself cannot tell the difference between an intentionally new name, and a misspelling of a name it already knows. But by reporting all new names it encounters, the Wolfram Language allows you to see whether any of them are mistakes.
| $NewSymbol | a function to be applied to the name and context of new symbols which are created |
When the Wolfram Language creates a new symbol, you may want it not just to print a message, but instead to perform some other action. Any function you specify as the value of the global variable $NewSymbol will automatically be applied to strings giving the name and context of each new symbol that the Wolfram Language creates.