モジュール構成と変数名の付け方
| モジュールと局所変数 | コンテキストとパッケージ |
| 局所定数 | Wolfram言語パッケージ |
| モジュールの動作の仕方 | パッケージ |
| 純関数と規則で使う変数 | パッケージのファイル |
| 数学のダミー変数 | パッケージの自動読込み |
| ブロックと局所値 | シンボルとコンテキストの名前による操作 |
| ブロックとモジュールの比較 | シンボル生成処理の内容確認 |
| コンテキスト |
しかし，特にプログラムの記述においては，必ずしもすべての変数を大域的なものとはしたくないことがある．例えば，同じxの名前を使い，2つのプログラムにある別々の2つの変数を参照したいかもしれない．このようなときは，xを各プログラムにおいて局所変数として扱われるようにしておく必要がある．
| Module[{x,y,…},body] | 局所変数 x, y, … を備えたモジュール |
モジュールの最も一般的な使いみちは，定義したい関数の中で一時的（臨時的）な変数を設けることである．そのような変数はモジュール内だけで有効な局所変数にしておくことが重要である．局所変数にしておかないと，同じ参照名を持つ変数が外部にある場合，競合してしまい思いも寄らない間違いを引き起してしまう．
あるモジュールで局所変数が設けられるとき，Wolfram言語はその変数に対しての値の割当ては行わない．このため，モジュールの外に同じ名前の大域変数がすでにあったとしても，それを純粋なシンボルとして使うことができる．
ここで，Lengthは単に1つの数を引数として受け取る：
| Module[{x=x0,y=y0,…},body] | モジュールの局所変数に初期値を割り当てる |
初期値の定義はモジュールのどの局所変数に対してでも行うことができる．初期値は常にモジュールが実行される前に評価される．このため，モジュールに対して局所的に定義された変数xがあっても，名前xがある初期値の設定を行うための式に現れるときは，大域のxが使われる．
| lhs:=Module[vars,rhs/;cond] | 右辺 rhs と条件式 cond の間で局所変数を共有する |
ある定義に対して/;条件式を設ける際は，一時的な変数を導入する必要がよく出てくる．多くの場合は，一時変数を定義の右辺にある本体式とで共有できるようにしたい．このような共有を行うには，条件式を含める形で定義の右辺をモジュールの角カッコに入れておく．
| With[{x=x0,y=y0,…},body] | 局所定数 x, y, … を定義する |
Moduleを使うと局所変数を設定し，それに値を割り当て．変更することができる．しかし，多くの場合，本当に必要なものは一度だけ値が割り当てられる局所定数だけである．Wolfram言語では，局所変数の設置は構成体Withを使い行うことができる．
With[{x=x0,…},body]の機能の仕方としては，まず，body が取り出され，次に，式中に現れる x 等の各オブジェクトがそれに対応した値 x0等で置換される．Withは一般化された演算子/.ととらえることができ，式でなくWolfram言語コードに適している．
Withを使う1つの大きな理由は，多くの場合，Moduleより読みやすい計算プログラムを書くことができるからである．Moduleを使うとすると，局所変数（例えば，x）の値を確認するには，x が参照されるたびに，そこまでの式をすべてトレースしなければならない．その点，Withを使うと，どこに x があってもその値は同じなので，単に初期値を見るだけでよい．コードをトレースする必要はない．
複数のネストされたWith構成体があるとき，同じ参照名の局所変数が複数存在してしまう場合がある．そのときは，常に，最も内側の部分に置かれた変数の定義が有効とされる．ModuleとWithは混ぜて使うことができる．そのときも，一般則として，有効とされる変数は最も内側の変数である．
ネストされたWith構成体で有効とされる変数は最も内側のものである：
x と body がいつ評価されるかの問題を除けば，With[{x=x0,…},body]は，基本的に式 body/.x->x0と同様に機能する．しかし，body に別のWith式やModule式があるとき，Withは特殊な動作を取る．ここで重要な点は，Withにある局所定数の間と，そして局所定数と大域オブジェクトの間で競合が起らないようにすることである．実際にどうすればこれができるかは「モジュールの動作の仕方」を参照のこと．
モジュールの動作は基本的に非常に単純である．モジュールが使われると，その都度，新規のシンボルが生成されモジュールの必要とする局所変数が表される．新規シンボルには，固有の名前が与えられる．名前は他のシンボル名と競合しないようにされる．つまり，ユーザにより指定された名前には$記号と固有の「シリアル番号」が加えられる．
Moduleは，各局所変数を表すために書式 x$nnn の名前を持つシンボルを生成する． |
通常の計算で，内部定義されるモジュール変数の名前を使うことはまずないであろう．しかし，モジュールを評価する際のダイアログ（カーネルとの対話）の開始とか，トレース機能を使ったモジュール内における各評価ステップのTrace では，内部定義の変数名が表示に使われることがある．
Traceを使うと，モジュール内で生成されるシンボルを見ることができる：
関数Uniqueを使うと，Moduleの場合と同じようにシンボルを新規に生成することができる．Uniqueが呼び出されるたびに，$ModuleNumberが増分されるため，新たに作られるシンボルは必ず固有の名前を持つようになる．
Uniqueが呼び出されるたびに，シリアル番号が1大きくなり，違う名前のシンボルが1つ得られる：
複数の名前のリストを使いUniqueを呼び出すと，作られるすべてのシンボルには同一のシリアル番号が与えられる：
Moduleで生成されたシンボルは，評価の目的において，他のシンボルと全く同様に機能する．しかし，これらのシンボルは，有効性を一時的にする属性Temporaryを持つため，使用されなくなった時点で消去される．モジュールの中で生成されるほとんどのシンボルは，そのモジュールの実行が完了する時点で除去される．例外として，戻り値として返されるシンボルだけは生き残る．
x$nnn 形式による名前の付け方は単なる規約である．ユーザ自身でこの形式を使いシンボルに名前を付けることもできる．ただし，そうして作成されたシンボルは，Moduleで生成されたものと競合してしまうかもしれない．
重要な点は，Moduleにより生成されるシンボルは，通常，現行のセッションだけで有効であることである．シリアル番号を決定するためのパラメータ$ModuleNumberは常に新たなセッションが開始されるときに再設定される．
このため，特に，生成されたシンボルを含んだ式をファイルに保存し，それらの式を別のセッションに読み込ませるとき，競合が起らないという保証は何もない．生成されたシンボルは一般的に一時的なものなので，実際にはあまり起こらない．競合に対処する方法として，一時的なシンボルが読み込まれるセッションの最初に，大きい値に$ModuleNumber（例えば2^($SystemWordLength-8)）を手動で設定するというものがある．
Module[vars,body]は，指定された局所変数を表すためのシンボルを生成すると，次に，これらのシンボルを適用することで本体式 body を評価していく．取られる第1ステップは，実際の式 body をモジュール内に現れる通りの形で抽出し，そして，Withを実行的に適用することで，各局所変数を適切な内部生成されたシンボルで置換している．このステップが終り次第，Moduleは，結果として得られた式を実際に評価する．
注意点として，Module[vars,body]は，内部生成されたシンボルを実際の式 body だけに挿入する．内部生成されたシンボルは body から呼び出されるが，body に具体的に現れないコードには挿入されない．
多くの場合，モジュールの設置は，書式Module[vars,body]に従って記述された明示的なWolfram言語への入力を使うことで行われるだろう．関数Moduleには属性HoldAllが付加されているので，実際にモジュールが実行されるまでは，本体 body は未評価のまま保持される．
ただし，モジュールを動的に構築することは可能である．新たなシンボルの生成や，それらの body への挿入は，モジュールが実際に実行されるときに初めて行われる．モジュールがWolfram言語への入力として与えられるときではない．
例えば，Function[{x},x+a]のような純関数を使うとき，x は，局所的な特定の名前を持つ「仮パラメータ」として扱いたい．同じことは，f[x_]->x^2のような規則や，f[x_]:=x^2のような定義に現れるx に対しても言える．
Wolfram言語では一律の処理法が取られるので，純関数のような構成体に現れる仮パラメータは常に局所化された名前を持つ．したがって，大域的な名前と競合することはない．基本的な考えとしては，必要ならば，形を x$とする名前を持つシンボルで仮パラメータを置換する．規約に従い，x$は大域変数として使ってはいけない．
純関数で仮パラメータを使うと，その名前は変更されると説明したが，そのような処理は場合によっては不必要である．基本的に，純関数において仮パラメータの名前が純関数の本体式に代入される式の部分と競合しなければ，特に名前を変更する必要はない．しかし，一律性を維持するため，必要ないときも，仮パラメータの名前は変更される．
「純関数」で説明したように，Wolfram言語の純関数は形式論理で使われる 
式のようなものである．Wolfram言語では，仮パラメータに対しての名前の変更を行うことで標準 
式の機能をすべて実現可能にしている．
式のようなものである．Wolfram言語では，仮パラメータに対しての名前の変更を行うことで標準 式の機能をすべて実現可能にしている．| Function[{x,…},body] | 局所パラメータ |
| lhs->rhs and lhs:>rhs | 局所パターン名 |
| lhs=rhs and lhs:=rhs | 局所パターン名 |
| With[{x=x0,…},body] | 局所定数 |
| Module[{x,…},body] | 局所変数 |
Wolfram言語には，いくつかの「スコープ（有効範囲）限定のための構成体」を備えている．これらを使うことで，特定の名前を局所化することができる．また，これらの構成体が混ぜて使われるとき，Wolfram言語は，競合を防ぐように適切な名前の変更を行う．
内側のWithにある局所変数は名前が変更され競合しないようになる：
f[x_]->x+yのような規則では右辺に現れる x は引数パターンx_に適合する．このため，x は規則に対して局所的な変数として扱われる．したがって，別の構成体で x を別のスコープに変更することはできない．
スコープを限定する構成体にWithを使うと，Wolfram言語は自動的に適切な名前の変更を行う．しかし，場合によっては，名前の変更をせずに，スコープを限定する構成体の中において代入操作を行いたい．そのようなときは演算子/.を使う．
f[x_]->rhs のような規則や，f[x_]:=rhs のような定義が適用されると，Wolfram言語は，右辺 rhs にあるすべての x に対して代入操作を施す．この代入操作は，演算子/.が実効的に使われて行われる．このため，この代入では，スコープ構成体によるスコープが効かなくなってしまう．ただし，あるスコープ構成体の内部のオブジェクトが代入操作により変更されるときは，そのスコープ構成体にある他の変数は名前が変更される．
数学の理論式を構築する際には，各種の局所化されたオブジェクト，つまり，「ダミー変数」を導入する必要がでる．ダミー変数は，モジュールや他のスコープを限定するための構成体を使うことで作成することができる．
数学のダミー変数の代表的なものに積分変数がある．形式的な積分を記述するとき，慣用の表記法では，特定名を持つある積分変数を導入する必要がある．この変数は，基本的に積分に「局所的」とされる．また，ダミー変数の名前は，任意の名前で構わないが，数式にある他の名前と競合してはならない．
多くの場合，ダミー変数は局所なままにしておき，数式の他の変数に干渉しないようにしておきたい．しかし，場合によっては，同じダミー変数を違った用途で使うときに，用途間で競合しないようにすることがより重要になる．
ベクトルやテンソルの積を構築する式では，ダミー変数を繰り返し使う必要が出てくる．「和の規約」にならうと，ちょうど2回現れるベクトルやテンソルの添数には，その添数の取り得る限りの値の中で総和が取られる．繰り返し使われる添数の実際の名前は何でも構わないが，もしも，繰り返し使われる添数が2つあるならば，競合しないような名前にしておく必要がある．
数学のいろいろな場面で，固有名を持つ変数を使う必要が出てくる．例えば，方程式の解を表すときがそうである．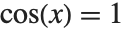
のような方程式には，
の形の解は無限に存在する．ここで，
はダミー変数であり，値は整数であれば何でもよい．
のような方程式には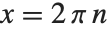， の形の解は無限に存在する．ここで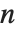， はダミー変数であり，値は整数であれば何でもよい．固有のオブジェクトが必要となるもうひとつの場面は「積分定数」を表すときである．積分を行うということは，実効的に導関数に関して方程式を解くことに相当する．一般に，方程式にはいくつもの可能な解が存在し，各解は加法的な「積分定数」により他の解と異なる．標準的なWolfram言語の積分関数Integrateは，常に，積分定数を付加しないで解を返すようになっている．しかし，ユーザ自身で，積分定数を導入すれば，モジュールを使い各定数を固有化しておく必要がある．
モジュールを使うことで，変数の名前を局所的なものとして扱うことができる．場合によっては，変数の参照名は大域的なものとしておき，変数の取る値だけを局所化したい．これを行うにはBlockを使う．
「モジュールと局所変数」で説明してあるように，Module[{x},body]において，変数 x は常に固有な名前を参照するように設定される．つまり，モジュールが使われるたびに固有とされ，また，大域変数 x からも固有とされるように x は名前が変更される．これに対して，Block[{x},body]では，x は大域的なスコープ x とされる．ただし，x の取る値は局所的なものとされる．したがって，ブロックが終了すると，x には昔の値が戻される．ブロック内ではどんな値でも割り当てることができる．
ブロックを使うと，実効的に「局在化された環境」を作り出すことができる．この環境では変数の値を一時的に変更することができる．あるブロックの実行中に評価される式は，そのブロックにある変数に対して現時点で定義されている現行値を使う．同じことは，ブロックで直接記述される本体の各式だけでなく，各式の評価により生成される式についても言える．
直接引数としては与えられないが，関数の動作には影響を与える，という働きを持つ大域変数が使えると便利な場合がある．一例として，帰納的な反復回数の上限を決定するための大域変数$RecursionLimitがある．この変数はすべての関数の評価に影響を及ぼすが，関数の直接の引数としては働かない．
大域変数に一度値が割り当てられると，特別に変更されるまでは，その値は変わらない．場合によっては，特定の計算だけとか計算の一部分だけで値を有効としたいときもある．それを行うにも，ブロックを使うことができる．
大域変数を使い，関数のパラメータへの値の割当ての他に，関数からの結果の蓄積を行うこともできる．つまり，大域変数をあるブロックに対して局所化しておくことで，ブロックから呼び出される関数からだけの結果を蓄積させることができる．
Block[{x},body]等のブロックが評価されるときは，x に割り当てられている現行値が除去される．このため，理論上は，ブロックの中では x を実質的な「シンボル的な変数」として扱うことができる．しかし，x を戻り値としてブロックから返すと，それはブロック評価前の外部の値により置換されてしまう．
ほとんどの従来型のプログラミング言語では，いわゆる「レキシカルなスコープの限定法」が使われ変数の有効範囲を指定するようになっている．この方法はWolfram言語のモジュールに相当する．シンボル処理系の言語にLISPがあるが，そこでは，「ダイナミックなスコープの限定」もできるようになっている．これは，Wolfram言語のブロックに相当している．
レキシカルな限定を行うと，変数の参照名は局所化され，プログラムコードの一部分だけでしか参照することができないようになる．これに対して，ダイナミックな限定を行うと，局所化は変数の値に対して行われ，値はプログラム実行における時間的な履歴の一区間だけで有効になる．
CやJavaのようなコンパイル系の言語ではコード体系と実行履歴体系をはっきりと区別することができる．シンボル処理系のWolfram言語では，この境界はやや曖昧である．それというのも，Wolfram言語では実行中のプログラムからダイナミックにコードを生成することも可能だからである．
モジュールModule[vars,body]を使うと，このモジュールがWolfram言語プログラムのコードとして実行されるときに初めて式 body が処理の対象になる．モジュールは式を調べ，変数 vars のいずれかが，明示的にコードに現れた時点で初めて局所化される．その後通常の評価が行われる．
ブロック式Block[vars,body]では式 body の形は無視される．その代り，それぞれの vars の現行の値が記録される．式 body が評価される間は vars の値はずっと局所的なものとされ，body の評価が終了するともとの値に戻される．
Wolfram言語では，「コンテキスト」と呼ばれる考え方が使われシンボルの名前を構成することができるようになっている．コンテキストは，Wolfram言語のパッケージを使うときに特に重要で，あるパッケージで導入されたシンボルの名前が他のシンボルの名前と競合しないようにするために使われる．ユーザ自身でパッケージを記述する場合や，市販パッケージの中身を変更するような場合には，コンテキストについて詳しい知識を持つ必要がある．
対象になるオブジェクトが何であれ，その正式名称は必ず2つの部分からなる．すなわち，完全名はコンテキスト名と簡略名（いわゆる名前）からなり，「context`short」の書式で記述される．Wolfram言語において，記号`は（ASCII文字コード番号は10進数の96）コンテキストマークと呼ばれる．
定義したいシンボルの種類に依存してコンテキストを使い分けるとよい．例えば，物理単位を表したシンボルには，特別なコンテキストPhysicalUnits`を使ったりすることができる．そうすると，単位記号の完全名はPhysicalUnits`Joule（ジュール）とかPhysicalUnits`Mole（モル）とかになる．
現行セッションの任意位置において，現行のコンテキスト$Contextは必ず1つだけある．シンボルが$ContextPath上の同じ短縮名を持つシンボルで隠されていない限り，そのコンテキストにあるシンボルはその簡略名を使うだけで参照することができる．
Wolfram言語のコンテキストは，いくつかの面で，多くのオペレーティングシステムで使われているファイルのディレクトリに似ている．例えば，ファイルを指定するには，ファイル名とディレクトリ名を一緒に指定すれば確実にできる．しかし，常に現行の作業ディレクトリが存在しており，それが現行のWolfram言語コンテキストに相当する．そのディレクトリにあるファイルなら，いちいちディレクトリ名を指定する必要はない．
多くのオペレーティングシステムにおけるディレクトリがそうであるように，Wolfram言語のコンテキストも階層構造を取っている．例えば，シンボルが3つのコンテキストからなる階層位置に置かれている場合，その正式名は，c1`c2`c3`name となる．
| context `name または c1`c2 … `name | 絶対指定コンテキスト |
| `name | 現行コンテキスト |
| `context`name または `c1`c2` … `name | 相対指定コンテキスト |
| name | 相対指定コンテキスト |
Wolfram言語のセッションが始まる時点では，コンテキストはGlobal`（大域的）にされる．普通は，このコンテキストにオブジェクトを作成していくことになる．例外として，Pi等の組込み定数はSystem`（システム）コンテキストに定義される．
Global`だけでなく，System`のようなよく使われるコンテキストは特別な操作なしで使うことができると便利である．そこで，Wolfram言語ではコンテキストの検索パスと呼ばれるオブジェクトが提供されている．Wolfram言語のセッションでは，現行コンテキストはパラメータ$Contextに登録される．検索パスは$ContextPathに保持される．コンテキスト名が検索パスにあれば，そのコンテキストにあるオブジェクトを参照するときに特にそのコンテキストを指定する必要はない．簡略名だけで指定できる．
Wolframシステムのシンボルに対するコンテキスト検索パスは，プログラムファイルを探すためのオペレーティングシステム上の検索パスに相当する．$Contextは$ContextPathの後に検索されるため，ファイルの検索パスに「.」が加わったものと考えることができる．
| Context[s] | シンボルのコンテキスト |
| $Context | 現行セッションにおける現行コンテキスト |
| $ContextPath | 現行コンテキスト検索パス |
| $ContextAliases | コンテキストのエイリアスのリスト |
| Contexts[] | すべてのコンテキストのリスト |
違うコンテキストならば，簡略名は同じであっても構わない．例えば，物理単位コンテキストPhysicalUnits`と生物コンテキストBiologicalOrganisms`と呼ばれるコンテキストを作ったとする．すると，そのどちらのコンテキストにも，Moleの同一名でシンボルを作成することができる．
簡略名だけで参照すると，通常，検索パスで先に現れるコンテキストにある同名のシンボルが選択される．このため，検索パスの後の方で現れるコンテキストに同名のシンボルがある場合や，現行のコンテキストに同盟のシンボルがある場合，これらのシンボルは隠されてしまう．隠されたシンボルを参照するには，コンテキストを含む完全名を指定する必要がある．
$ContextPathで既存のシンボルを隠してしまうような新しいシンボルを導入した場合，メッセージが出力される．また，ノートブックフロントエンドが赤く色付けすることで隠されたシンボルを警告する．
既存のシンボルを隠してしまうようなシンボルを一度導入してしまうと，$ContextPathを変更して検索パス指定のコンテキストの並び順を変えるか，シンボル自体を除去するまでは遮蔽効果が続いてしまう．除去するには単にシンボルの持つ値を消すだけでは不十分で，シンボル自体を消し去る必要がある．除去はRemove[s]を使い行う．
シンボル名が出力されるとき，Wolfram言語はその正式名と簡略名のどちらかを出力に使う．実際に出力される名前は，現行コンテキスト$Contextと検索パス$ContextPathの現行設定に対応して，該当シンボルを取得するために必要な名前である．
簡略名を入力し，その名前に相当するシンボルがどのコンテキストにも存在しない場合は，それは新規のシンボルとして生成される．そのとき，新規シンボルは$Contextにある現行コンテキストにおいて作られる．
一般規約として，パッケージの読込み時に定義される新規のシンボルはすべて個別のコンテキスト，つまり，そのパッケージに関連付けられたコンテキストに入れられることになっている．パッケージが読み込まれる際は，適切なコンテキストが検索パス$ContextPathの先頭に付け加えられる．
検索パス$ContextPathの先頭にこのパッケージのコンテキストが付け足される：
パッケージにあるシンボルには非常に長い参照名を持つものが数多くある．しかし，それらの参照は，ほとんどの場合，簡略名だけで間に合う．パッケージが読み込まれると同時に，パッケージのコンテキストが$ContextPathに付け足されるからである．簡略名を入力すると，パスが自動検索されるため適切なコンテキストが判明する．
それでも問題が起らないとは限らない．2つのパッケージを使い，そのどちらにも同じ簡略名の変数があると競合が起ってしまう．実際にパッケージを読み込ませると，2つ目が読み込まれる際には警告が発せられ，新しいパッケージのシンボルにより先のパッケージのシンボルが隠蔽されてしまうという旨が表示される．
競合状態は何もパッケージ間だけで起るものではない．読み込まれたパッケージとユーザが現行セッションで直接入力したものとの間でも起り得る．現行コンテキストで何かシンボルを定義したとすると，読み込むパッケージに同名のシンボルがあると，後者が隠されてしまうことがある．理由は，検索パスのコンテキストが現行コンテキストより優先されるためである．
パッケージのScalarQが使われる：
シンボルの隠蔽問題が起ったら，まず，Remove[s]を使い必要でなくなったシンボルを除去する．それでも問題が解消しないときは，検索パス$ContextPathや現行コンテキスト$Contextを再編集し，必要なシンボルを含むコンテキストが先に検索されるようにする．
| $Packages | 現行Wolfram言語セッションに読み込まれている全パッケージのコンテキストがリスト形式で登録してある |
Wolfram言語の最も重要な特徴のひとつに拡張性が非常に高いということがある．数学関数や他の標準的な機能が組み込まれてはいるが，Wolfram言語を使うことで，機能性をさらに向上することが可能になっている．
そのようなとき，必要な関数がパッケージに入っているかもしれない．パッケージはWolfram言語で書かれたプログラムファイルであり，Wolfram言語に特定の応用分野について「教授する」定義の集まりから構成されている．
パッケージに入っている関数を使うには，まず，パッケージをWolfram言語に読み込ませる必要がある．やり方の詳細に関しては「外部プログラム」を参照してほしい．パッケージを参照する際に必要となる名前の指定に関する約束事が説明してある．
関数ProvablePrimeQは，このパッケージで定義されている：
パッケージ間での関数名の衝突のような問題に関連した微妙なことが多数ある．これは「コンテキストとパッケージ」で詳しく触れる．ここで言及しておきたいのは，まだ読み込まれていないパッケージの中にある関数を参照してはならないということである．誤って参照してしまうと，Wolfram言語は重複した名前についての警告メッセージを表示し，最後に定義したものを使う．つまり，自分が使いたい関数が使われないということである．パッケージの関数を使うのである．このようなときは，Remove["name"]を実行すると，パッケージの関数を除去することができる．
| Remove["name"] | 誤って定義した関数を除去 |
パッケージを追加することでWolfram言語の機能を拡張できるということは，裏を返せばどこまでが「Wolfram言語本来の部分」か，というような境界ができないことを示している．実際には，パッケージの関数と組込み関数の間には全く違いがない．
Wolfram言語の中核に組み込まれている関数の多くは，実際にはWolfram言語パッケージとして実装されている．それでも，一部のWolframシステムを除いて，これらのパッケージは先読みされるので，関数は常に使える状態にある．
Wolfram言語本来の部分をさらに不明確にするものとして，次の機能がある．「パッケージの自動読込み」でやり方を説明するが，パッケージにある関数を参照するたびに関数の定義がパッケージから自動的に読み込まれるようにすることができる．関数が参照されなければ，関数は存在しないままだが，一度参照されると，その定義はパッケージから自動的に読み込まれる．
それでも，ほとんどのWolframシステムのバージョンには標準でWolfram言語パッケージが添付されているため，より多くの関数が定義済みになっている．それらの関数を使うには，パッケージを手動で読み込ませる必要がある．
適当なWolframシステムを設定することで，このようなパッケージを先読みさせたり，必要なときに自動的に読み込ませることも可能である．そうすると，組込み関数と同様に扱える関数が多くなるが，Wolfram言語のレファレンスページではこのような関数については説明しない．
最後に，パッケージとノートブックの関係について触れておく．これらはともに使用中のコンピュータシステムにファイルとして保存され，またWolframシステムに読み込ませることができる．両者の違いは，ノートブック文書は表示される（ノートブックフロントエンドを使って）ためにあるのに対して，パッケージはWolfram言語の入力のためにある，ということである．それでも，実際，多くのノートブックはパッケージとみなされる部分を含み，それらはWolfram言語の入力として使われる一連の定義を持っている．また，ノートブックの自動保存に対応するパッケージの設定もある．
代表的なWolfram言語パッケージにおいて新規に生成されるシンボルは2種類ある．そのひとつは，パッケージ外部への送出（エキスポートと呼ぶ）に使われるシンボルで，もうひとつは，パッケージ内部だけで使われるシンボルである．2つを区別するには別々のコンテキストを指定する必要がある．
デフォルトで，外部送出用のシンボルは，Package`という名前のコンテキストに入れられる．パッケージの読込み時にこのコンテキストが自動的に検索パスに付け加えられ，それを参照するには簡略名だけでよくなるようになっている．
また，内部処理だけで使うシンボルはプライベートなコンテキスト Package`Private`に導入される．このコンテキストは検索パスには追加されない．このため，シンボルの参照には正式名を使う必要がある．
| Package` | 外部送出用パッケージのシンボルを導入するコンテキスト |
| Package`Private` | 内部処理用パッケージのシンボルを導入するコンテキスト |
| System` | 組込みシンボルのあるコンテキスト |
| Needed1`
,
Needed2`
,
…
| パッケージで必要な他のコンテキスト |
パッケージからコンテキストを設定するための命令書式および手順がある．それらを使い，現行コンテキスト$Contextと検索パス$ContextPathを適切に設定することで，新規シンボルを必要なコンテキストに導入できる．
| BeginPackage["Package`"] | パッケージ名 Package` を現行コンテキストにし，検索パスにはシステムコンテキストSystem`だけを指定する |
| f::usage="text"
,
…
| 外部送出用オブジェクトを作成する |
| Begin["`Private`"] | 現行コンテキストを Package`Private`内だけで有効なものにする |
| f[args]=value
,
…
| パッケージの定義式本体を記述する |
| End[] | 定義記述を終えて，コンテキストを Package`に戻す |
| EndPackage[] | パッケージコンテキスト Package`を検索パスの先頭に追加してパッケージを終了する |
BeginPackage["Collatz`"]
Collatz::usage =
"Collatz[n] gives a list of the iterates in the 3n+1 problem,
starting from n. The conjecture is that this sequence always
terminates."
Begin["`Private`"]
Collatz[1] := {1}
Collatz[n_Integer] := Prepend[Collatz[3 n + 1], n] /; OddQ[n] && n > 0
Collatz[n_Integer] := Prepend[Collatz[n/2], n] /; EvenQ[n] && n > 0
End[ ]
EndPackage[ ]
パッケージの最初の部分でusageメッセージを定義するのが，エキスポートしたい記号が適切なコンテキストで作られていることを確実にする一般的な方法である．このメッセージを定義することで，そこで挙げた記号のみがエキスポートしたい記号となる．この記号はその時点で現行の Package`で作られる．
パッケージでは通常数多くの関数定義を行い，そのためパラメータや一時変数等の各種シンボルを導入しておく必要がある．これらのシンボルはデフォルトでパッケージのプライベートコンテキスト Package`Private`に入れておくことになっている．なお，パッケージ読込みの際は，プライベートコンテキストは検索パスへ追加されない．
パッケージにあるコマンドEndPackageが実行される時点でパッケージのコンテキストが検索パスに追加される：
現行セッションのどこでも，<<context`の命令書式を使い必要なパッケージを読み込ませることが可能である．（パッケージファイルにアクセスする上でシステム非依存のコンテキスト名ををシステムに依存したファイル名に変換する必要がある．詳しくは「パッケージのファイル」を参照のこと．）ただし，必要なときだけ自動的にパッケージが読み込まれるようになるとより便利である．Needs["context`"]と呼ばれる機能が提供されているので，それを使い必要なコンテキストを指定しておく．すると，そのコンテキストが現行パッケージのリスト$Packagesになければ，パッケージが自動的に読み込まれる．
| Get["context`"] または <<context` | コンテキストに対応したパッケージを読み込む |
| Needs["context`"] | コンテキストが現行パッケージリスト$Packagesになければ対応したパッケージを読み込む |
| BeginPackage["Package`",{"Needed1`", … }] | |
システムコンテキストSystem`の他にコンテキストを検索パスに指定する | |
BeginPackage["Package`"]を使うとき，パッケージ名の引数だけを与えると，組込みシンボル用のコンテキストの他には，Package`のコンテキストしか検索パスに追加されない．もし，ユーザの作成するパッケージに別のパッケージの関数に依存する定義式があると，そのパッケージのコンテキストも検索パスに加えておかなければいけない．それをするには，BeginPackageの命令に第2の引数として必要なコンテキスト名をリスト形式で列記する．すると，BeginPackageはNeedsの機能を自動的に使いコンテキストの作成に必要なパッケージを読み込み，検索パスに必要なコンテキストを加える仕組みになっている．
Beginのようなコンテキスト操作の命令を実行すると，ユーザの入力するシンボル名の解釈が変わる．ただし，変更は命令の後に続く式から有効になる．Wolfram言語では，式は一括で読み込まれるので，式の部分評価が始まる前に，式にあるシンボルの参照名がすべて解釈されることになっている．このため，式にBegin命令があっても，命令が実行される前に式の参照名が先に解釈されてしまう．つまり，Begin命令を使ってもその場ではコンテキスト変更の効果は得ることができない．
パッケージにある関数を実行する際は，TraceDialogを使うと対話モードでコンテキスト命令が使える．関数の使う引数や一時変数は，通常，パッケージのプライベートコンテキストにある．このコンテキストは検索パスには指定されてないので，引数や変数は正式名で表示される．また，それらを参照するには正式名を使う必要がある．そこで，ダイアログを設け，Begin["Package`Private`"]の命令を実行すればパッケージのプライベートコンテキストを現行のものにできる．そして，引数等の表示では簡略名が使われるようになり，参照するにも簡略名だけでよくなる．
基本的な考え方は，コンピュータシステムのそれぞれにWolfram言語コンテキストの名前に対応するファイル名の約束がある．したがって，コンテキストを使ってファイルを参照すると，使っているWolfram言語のバージョンがコンテキスト名をコンピュータシステムに合わせたファイル名に変換する．
| name.mx | DumpSave形式のファイル |
| name.mx/$SystemID/name.mx | ユーザのコンピュータシステムにおけるDumpSave形式のファイル |
| name.m | Wolfram言語のソース形式のファイル |
| name/init.m | 指定したディレクトリの初期化ファイル |
| dir/… | $Pathに指定する別のディレクトリのファイル |
Wolfram言語では<<name`でファイルの適切なバージョンを読み込む．まず，使っているコンピュータシステムに最適化されている name.mxという名前を持つファイルを使うことを試み，それが見付からないときは，通常のシステムに依存しないWolfram言語入力が書かれた name.mの形のファイルを読み込む．
name がディレクトリのとき，Wolfram言語はそのディレクトリにある初期化ファイルinit.mを読む．init.mファイルの目的は，たくさんの別々のファイルからなるWolfram言語パッケージの設定を行う便利な方法を提供することである．コマンド<<name`を入力すると，init.mが読み込まれてパッケージ全体の初期化が行われ，必要なファイルがすべて読み込まれる．
他のチュートリアルでは<<package およびNeeds[package]を使ってWolfram言語パッケージを明示的にロードする方法を説明した．しかし，ある特定のパッケージが必要なときに自動的にそれがロードされるようにWolfram言語を設定しておいた方がよい場合もある．
パッケージを自動で読み込み，パッケージに定義されているシンボルを参照するには，DeclarePackageと呼ばれるパッケージを宣言する機能が使える．参照したいシンボルを宣言しておくと，実際に参照するときに必要なパッケージが自動的に読み込まれる．
| DeclarePackage["context`",{"name1","name2",…}] | |
シンボル名 namei が参照されると，コンテキストのパッケージを自動的に読み込む | |
VariationalDを参照すると，パッケージが自動的に読み込まれる：
読み込ませたいパッケージがたくさんあるときは，必要なDeclarePackageの宣言文を盛り込んだ「参照名ファイル」を別途用意しておき，どのシンボルの参照があったらどのパッケージを読み込むか指定しておくと便利である．そうすれば，計算セッションを始める際に参照名ファイルだけを読み込むだけで自動読込みの準備が完了する．
関数DeclarePackageの働き方として，宣言時にすぐ指定シンボルが生成され，Stub（スタブ）と呼ばれる特殊な属性が同シンボルに付加される．そして，実際の計算セッションで，宣言シンボルを参照すると，Stub属性により対応パッケージを自動的に読み込むように判断される．
| Symbol["name"] | 名前でシンボルを作成する |
| SymbolName[symb] | シンボルの参照名を検索する |
| NameQ["form"] | 文字列 form にマッチする名前のシンボルがあるかどうかを判定する |
| Names["form"] | 文字列 form にマッチする名前を持つシンボルをすべて列挙する |
| Contexts["form`"] | 文字列 form にマッチする名前を持つコンテキストを列挙する |
| Clear["form"] | 文字列 form にマッチする参照名を持つすべてのシンボルの値を消去する |
| Clear["context`*"] | コンテキストにあるすべてのシンボルの値を消去する |
| Remove["form"] | 文字列 form にマッチする参照名を持つすべてのシンボルを完全に除去する |
| Remove["context`*"] | コンテキストにあるすべてのシンボルを完全に除去する |
| Remove["Global`*"] | 大域コンテキストGlobal`にあるシンボルすべてを完全に除去する |
特にコンテキスト指定をしていなければ，ユーザの導入するシンボルは大域コンテキストGlobal`に設けられる．Remove["Global`*"]と入力すれば，作成したすべてのシンボルが一括除去できる．組込み関数はシステムコンテキストSystem`にあるから除去されることはない．
| On[General::newsym] | シンボルを新規に生成する際にその旨を表示し，内容を確認できるようにする |
| Off[General::newsym] | シンボルが新規に生成する際にメッセージ表示を停止する |
内容が確認できれば，タイプミス等の誤りを見付けるのにも便利だろう．Wolfram言語自体は入力されたものがタイプミスかどうか判別できない．生成内容を表示させるようにしておけば，少なくともユーザ自身で入力の正確性を確認できる．
| $NewSymbol | 新規にシンボルを生成するたびに実行する，シンボルの参照名とコンテキスト名を引数とした関数を指定する |
新しくシンボルを作成するときは，単にシンボル内容を表示させるだけでなく，特別な処理を行いたいときもあるだろう．そのようなときは，大域変数$NewSymbolを使い，それに処理を施す関数を割り当てておくと，新規のシンボルが生成されるたびにシンボルの参照名とコンテキスト名の文字列が関数の引数として自動的に適用されるようになる．
