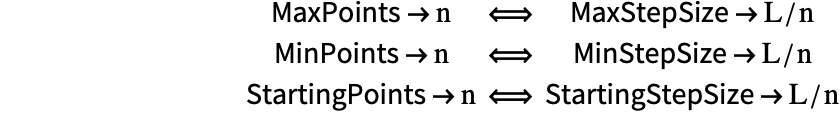The Numerical Method of Lines
Introduction
The numerical method of lines is a technique for solving partial differential equations by discretizing in all but one dimension and then integrating the semi-discrete problem as a system of ODEs or DAEs. A significant advantage of the method is that it allows the solution to take advantage of the sophisticated general-purpose methods and software that have been developed for numerically integrating ODEs and DAEs. For the PDEs to which the method of lines is applicable, the method typically proves to be quite efficient.
It is necessary that the PDE problem be well posed as an initial value (Cauchy) problem in at least one dimension, since the ODE and DAE integrators used are initial value problem solvers. This rules out purely elliptic equations such as Laplace's equation but leaves a large class of evolution equations that can be solved quite efficiently.
A simple example illustrates better than mere words the fundamental idea of the method. Consider the following problem (a simple model for seasonal variation of heat in soil):
This is a candidate for the method of lines since you have the initial value ![]() .
.
Problem (1) will be discretized with respect to the variable ![]() using second-order finite differences, in particular using the following approximation:
using second-order finite differences, in particular using the following approximation:
Even though finite difference discretizations are the most common, there is certainly no requirement that discretizations for the method of lines be done with finite differences; finite volume or even finite element discretizations can also be used.
To use the discretization shown, choose a uniform grid ![]() with spacing
with spacing ![]() such that
such that ![]() . Let
. Let ![]() be the value of
be the value of ![]() . For the purposes of illustrating the problem setup, a particular value of
. For the purposes of illustrating the problem setup, a particular value of ![]() is chosen.
is chosen.
For ![]() , you can use the centered difference formula (2) to obtain a system of ODEs. However, before doing this, it is useful to incorporate the boundary conditions.
, you can use the centered difference formula (2) to obtain a system of ODEs. However, before doing this, it is useful to incorporate the boundary conditions.
The Dirichlet boundary condition at ![]() can easily be handled by simply defining
can easily be handled by simply defining ![]() as a function of
as a function of ![]() . An alternative option is to differentiate the boundary condition with respect to time and add it to the boundary condition. In this example, the latter method will be used.
. An alternative option is to differentiate the boundary condition with respect to time and add it to the boundary condition. In this example, the latter method will be used.
The Neumann boundary condition at ![]() is a little more difficult. With second-order differences, one way to handle it is with reflection: imagine that you are solving the problem on the interval
is a little more difficult. With second-order differences, one way to handle it is with reflection: imagine that you are solving the problem on the interval ![]() with the same boundary conditions at
with the same boundary conditions at ![]() and
and ![]() . Since the initial condition and boundary conditions are symmetric with respect to
. Since the initial condition and boundary conditions are symmetric with respect to ![]() , the solution should be symmetric with respect to
, the solution should be symmetric with respect to ![]() for all time, and so symmetry is equivalent to the Neumann boundary condition at
for all time, and so symmetry is equivalent to the Neumann boundary condition at ![]() . Thus,
. Thus, ![]() , so
, so ![]() .
.
Now the PDE has been partially discretized into an ODE initial value problem that can be solved by the ODE integrators in NDSolve.
The plot indicates why this technique is called the numerical "method of lines".
The solution in between lines can be found by interpolation. When NDSolve computes the solution for the PDE, the result is a two-dimensional InterpolatingFunction.
The setting ![]() used did not give a very accurate solution. When NDSolve computes the solution, it uses spatial error estimates on the initial condition to determine what the grid spacing should be. The error in the temporal (or at least time-like) variable is handled by the adaptive ODE integrator.
used did not give a very accurate solution. When NDSolve computes the solution, it uses spatial error estimates on the initial condition to determine what the grid spacing should be. The error in the temporal (or at least time-like) variable is handled by the adaptive ODE integrator.
In the example (1), the distinction between time and space was quite clear from the problem context. Even when the distinction is not explicit, this tutorial will refer to "spatial" and "temporal" variables. The "spatial" variables are those to which the discretization is done. The "temporal" variable is the one left in the ODE system to be integrated.
option name | default value | |
| TemporalVariable | Automatic | what variable to keep derivatives with respect to the derived ODE or DAE system |
| Method | Automatic | what method to use for integrating the ODEs or DAEs |
| SpatialDiscretization | Automatic | what method to use for spatial discretization |
| DifferentiateBoundaryConditions | True | whether to differentiate the boundary conditions with respect to the temporal variable |
| ExpandEquationsSymbolically | False | whether to expand the effective function symbolically or not |
| DiscretizedMonitorVariables | False | whether to interpret dependent variables given in WhenEvent, in monitors like StepMonitor, or in method options for methods like Projection as functions of the spatial variables or vectors representing the spatially discretized values |
Options for NDSolve`MethodOfLines.
Use of some of these options requires further knowledge of how the method of lines works and will be explained in the sections that follow.
The methods currently implemented for spatial discretization are "TensorProductGrid" and "FiniteElement". Both methods have their own set of options that can be used to control details of the discretization process. The "FiniteElement" method is very general and works with arbitrarily shaped regions; it has its own set of tutorials. The following sections in this tutorial focus on using the "TensorProductGrid" discretization.
Spatial Derivative Approximations
Finite Differences
The essence of the concept of finite differences is embodied in the standard definition of the derivative
where instead of passing to the limit as ![]() approaches zero, the finite spacing to the next adjacent point,
approaches zero, the finite spacing to the next adjacent point, ![]() , is used so that you get an approximation
, is used so that you get an approximation
The difference formula can also be derived from Taylor's formula,
which is more useful since it provides an error estimate (assuming sufficient smoothness)
An important aspect of this formula is that ![]() must lie between
must lie between ![]() and
and ![]() so that the error is local to the interval enclosing the sampling points. It is generally true for finite difference formulas that the error is local to the stencil, or set of sample points. Typically, for convergence and other analysis, the error is expressed in asymptotic form:
so that the error is local to the interval enclosing the sampling points. It is generally true for finite difference formulas that the error is local to the stencil, or set of sample points. Typically, for convergence and other analysis, the error is expressed in asymptotic form:
This formula is most commonly referred to as the first-order forward difference. The backward difference would use ![]() .
.
Taylor's formula can easily be used to derive higher-order approximations. For example, subtracting
and solving for ![]() gives the second-order centered difference formula for the first derivative,
gives the second-order centered difference formula for the first derivative,
If the Taylor formulas shown are expanded out one order farther and added and then combined with the formula just given, it is not difficult to derive a centered formula for the second derivative
Note that while having a uniform step size ![]() between points makes it convenient to write out the formulas, it is certainly not a requirement. For example, the approximation to the second derivative is in general
between points makes it convenient to write out the formulas, it is certainly not a requirement. For example, the approximation to the second derivative is in general
where ![]() corresponds to the maximum local grid spacing. Note that the asymptotic order of the three-point formula has dropped to first order; that it was second order on a uniform grid is due to fortuitous cancellations.
corresponds to the maximum local grid spacing. Note that the asymptotic order of the three-point formula has dropped to first order; that it was second order on a uniform grid is due to fortuitous cancellations.
In general, formulas for any given derivative with asymptotic error of any chosen order can be derived from the Taylor formulas as long as a sufficient number of sample points are used. However, this method becomes cumbersome and inefficient beyond the simple examples shown. An alternate formulation is based on polynomial interpolation: since the Taylor formulas are exact (no error term) for polynomials of sufficiently low order, so are the finite difference formulas. It is not difficult to show that the finite difference formulas are equivalent to the derivatives of interpolating polynomials. For example, a simple way of deriving the formula just shown for the second derivative is to interpolate a quadratic and find its second derivative (which is essentially just the leading coefficient).
In this form of the formula, it is easy to see that it is effectively a difference of the forward and backward first-order derivative approximations. Sometimes it is advantageous to use finite differences in this way, particularly for terms with coefficients inside of derivatives, such as ![]() , which commonly appear in PDEs.
, which commonly appear in PDEs.
Another property made apparent by considering interpolation formulas is that the point at which you get the derivative approximation need not be on the grid. A common use of this is with staggered grids, where the derivative may be wanted at the midpoints between grid points.
The fourth-order error coefficient for this formula is ![]() versus
versus ![]() for the standard fourth-order formula derived next. Much of the reduced error can be attributed to the reduced stencil size.
for the standard fourth-order formula derived next. Much of the reduced error can be attributed to the reduced stencil size.
In general, a finite difference formula using ![]() points will be exact for functions that are polynomials of degree
points will be exact for functions that are polynomials of degree ![]() and have asymptotic order at least
and have asymptotic order at least ![]() . On uniform grids, you can expect higher asymptotic order, especially for centered differences.
. On uniform grids, you can expect higher asymptotic order, especially for centered differences.
Using efficient polynomial interpolation techniques is a reasonable way to generate coefficients, but B. Fornberg has developed a fast algorithm for finite difference weight generation [F92], [F98], which is substantially faster.
In [F98], Fornberg presents a one-line Wolfram Language formula for explicit finite differences.
Here ![]() is the order of the derivative,
is the order of the derivative, ![]() is the number of grid intervals enclosed in the stencil, and
is the number of grid intervals enclosed in the stencil, and ![]() is the number of grid intervals between the point at which the derivative is approximated and the leftmost edge of the stencil. There is no requirement that
is the number of grid intervals between the point at which the derivative is approximated and the leftmost edge of the stencil. There is no requirement that ![]() be an integer; noninteger values simply lead to staggered grid approximations. Setting
be an integer; noninteger values simply lead to staggered grid approximations. Setting ![]() to be
to be ![]() always generates a centered formula.
always generates a centered formula.
A table of some commonly used finite difference formulas follows for reference.
Finite difference formulas on uniform grids for the first derivative.
Finite difference formulas on uniform grids for the second derivative.
One thing to notice from this table is that the farther the formulas get from centered, the larger the error term coefficient, sometimes by factors of hundreds. For this reason, sometimes where one-sided derivative formulas are required (such as at boundaries), formulas of higher order are used to offset the extra error.
NDSolve`FiniteDifferenceDerivative
Fornberg [F92], [F98] also gives an algorithm that, though not quite so elegant and simple, is more general and, in particular, is applicable to nonuniform grids. It is not difficult to program in the Wolfram Language, but to make it as efficient as possible, a new kernel function has been provided as a simpler interface (along with some additional features).
| NDSolve`FiniteDifferenceDerivative[Derivative[m],grid,values] | |
| approximate the m th-order derivative for the function that takes on values on the grid | |
| NDSolve`FiniteDifferenceDerivative[Derivative[m1,m2,…,mn],{grid1,grid2,…,gridn},values] | |
| approximate the partial derivative of order (m1, m2, …, mn) for the function of n variables that takes on values on the tensor product grid defined by the outer product of (grid1, grid2, …, gridn) | |
| NDSolve`FiniteDifferenceDerivative[Derivative[m1,m2,…,mn],{grid1,grid2,…,gridn}] | |
| compute the finite difference weights needed to approximate the partial derivative of order (m1, m2, …, mn) for the function of n variables on the tensor product grid defined by the outer product of (grid1, grid2, …, gridn); the result is returned as an NDSolve`FiniteDifferenceDerivativeFunction, which can be repeatedly applied to values on the grid | |
Finding finite difference approximations to derivatives.
The derivatives at the endpoints are computed using one-sided formulas. The formulas shown in the previous example are fourth-order accurate, which is the default. In general, when you use a symbolic grid and/or data, you get symbolic formulas. This is often useful for doing analysis on the methods; however, for actual numerical grids, it is usually faster and more accurate to give the numerical grid to NDSolve`FiniteDifferenceDerivative rather than using the symbolic formulas.
In multiple dimensions, NDSolve`FiniteDifferenceDerivative works on tensor product grids, and you only need to specify the grid points for each dimension.
Note that the values need to be given in a matrix corresponding to the outer product of the grid coordinates.
NDSolve`FiniteDifferenceDerivative does not compute weights for sums of derivatives. This means that for common operators like the Laplacian, you need to combine two approximations.
option name | default value | |
| "DifferenceOrder" | 4 | asymptotic order of the error |
| PeriodicInterpolation | False | whether to consider the values as those of a periodic function with the period equal to the interval enclosed by the grid |
Options for NDSolve`FiniteDifferenceDerivative.
When using PeriodicInterpolation->True, you can omit the last point in the values since it should always be the same as the first. This feature is useful when solving a PDE with periodic boundary conditions.
Fourth-order differences typically provide a good balance between truncation (approximation) error and roundoff error for machine precision. However, there are some applications where fourth-order differences produce excessive oscillation (Gibb's phenomena), so second-order differences are better. Also, for high precision, higher-order differences may be appropriate. Even values of "DifferenceOrder" use centered formulas, which typically have smaller error coefficients than noncentered formulas, so even values are recommended when appropriate.
NDSolve`FiniteDifferenceDerivativeFunction
When computing the solution to a PDE, it is common to repeatedly apply the same finite difference approximation to different values on the same grid. A significant savings can be made by storing the necessary weight computations and applying them to the changing data. When you omit the (third) argument with function values in NDSolve`FiniteDifferenceDerivative, the result will be an NDSolve`FiniteDifferenceDerivativeFunction, which is a data object that stores the weight computations in an efficient form for future repeated use.
| NDSolve`FiniteDifferenceDerivative[{m1,m2,…},{grid1,grid2,…}] | |
| compute the finite difference weights needed to approximate the partial derivative of order (m1, m2, …) for the function of n variables on the tensor product grid defined by the outer product of (grid1, grid2, …); the result is returned as an NDSolve`FiniteDifferenceDerivativeFunction object | |
| NDSolve`FiniteDifferenceDerivativeFunction[Derivative[m],data] | |
| a data object that contains the weights and other data needed to quickly approximate the m th-order derivative of a function; in the standard output form, only the Derivative[m] operator it approximates is shown | |
| NDSolve`FiniteDifferenceDerivativeFunction[data][values] | |
| approximate the derivative of the function that takes on values on the grid used to determine data | |
Computing finite difference weights for repeated use.
Note that the standard output form is abbreviated and only shows the derivative operators that are approximated.
This function is only applicable for values defined on the particular grid used to construct it. If your problem requires changing the grid, you will need to use NDSolve`FiniteDifferenceDerivative to generate weights each time the grid changes. However, when you can use NDSolve`FiniteDifferenceDerivativeFunction objects, evaluation will be substantially faster.
An NDSolve`FiniteDifferenceDerivativeFunction can be used repeatedly in many situations. As a simple example, consider a collocation method for solving the boundary value problem
on the unit interval. This simple method is not necessarily the best way to solve this particular problem, but it is useful as an example.
Since the setup for this problem is so simple, it is easy to compare various alternatives. For example, to compare the solution above, which used the default fourth-order differences, to the usual use of second-order differences, all that needs to be changed is the "DifferenceOrder".
One way to determine which is the better solution is to study the convergence as the grid is refined. This is discussed to some extent in "Differentiation Matrices".
While the most vital information about an NDSolve`FiniteDifferenceDerivativeFunction object, the derivative order, is displayed in its output form, sometimes it is useful to extract this and other information from an NDSolve`FiniteDifferenceDerivativeFunction, say for use in a program. The structure of the way the data is stored may change between versions of the Wolfram Language, so extracting the information by using parts of the expression is not recommended. A better alternative is to use any of the several method functions provided for this purpose.
Let FDDF represent an NDSolve`FiniteDifferenceDerivativeFunction[data] object.
| FDDF@"DerivativeOrder" | get the derivative order that FDDF approximates |
| FDDF@"DifferenceOrder" | get the list with the difference order used for the approximation in each dimension |
| FDDF@"PeriodicInterpolation" | get the list with elements True or False indicating whether periodic interpolation is used for each dimension |
| FDDF@"Coordinates" | get the list with the grid coordinates in each dimension |
| FDDF@"Grid" | form the tensor of the grid points; this is the outer product of the grid coordinates |
| FDDF@"DifferentiationMatrix" | compute the sparse differentiation matrix mat such that mat.Flatten[values] is equivalent to Flatten[FDDF[values]] |
Method functions for exacting information from an NDSolve`FiniteDifferenceDerivativeFunction[data] object.
Any of the method functions that return a list with an element for each of the dimensions can be used with an integer argument dim, which will return only the value for that particular dimension such that FDDF@method[dim]=(FDDF@method)[[dim]].
The following examples show how you might use some of these methods.
Note that the rank of the grid point tensor is one more than the dimensionality of the tensor product. This is because the three coordinates defining each point are in a list themselves. If you have a function that depends on the grid variables, you can use Apply[f,fddf["Grid"],{n}] where n=Length[fddf["DerivativeOrder"]] is the dimensionality of the space in which you are approximating the derivative.
For a moderate-sized tensor product grid like the example here, using Apply is reasonably fast. However, as the grid size gets larger, this approach may not be the fastest because Apply can only be used in limited ways with the Wolfram Language compiler and hence, with packed arrays. If you can define your function so you can use Map instead of Apply, you may be able to use a CompiledFunction since Map has greater applicability within the Wolfram Language compiler than does Apply.
An even better approach, when possible, is to take advantage of listability when your function consists of operations and functions which have the Listable attribute. The trick is to separate the ![]() ,
, ![]() , and
, and ![]() values at each of the points on the tensor product grid. The fastest way to do this is using Transpose[fddf["Grid"],RotateLeft[Range[n+1]]], where n=Length[fddf["DerivativeOrder"]] is the dimensionality of the space in which you are approximating the derivative. This will return a list of length n, which has the values on the grid for each of the component dimensions separately. With the Listable attribute, functions applied to this will thread over the grid.
values at each of the points on the tensor product grid. The fastest way to do this is using Transpose[fddf["Grid"],RotateLeft[Range[n+1]]], where n=Length[fddf["DerivativeOrder"]] is the dimensionality of the space in which you are approximating the derivative. This will return a list of length n, which has the values on the grid for each of the component dimensions separately. With the Listable attribute, functions applied to this will thread over the grid.
The example timings show that using the CompiledFunction is typically much faster than using Apply and taking advantage of listability is a little faster yet.
Pseudospectral Derivatives
The maximum value the difference order can take on is determined by the number of points in the grid. If you exceed this, a warning message will be given and the order reduced automatically.
Using a limiting order is commonly referred to as a pseudospectral derivative. A common problem with these is that artificial oscillations (Runge's phenomena) can be extreme. However, there are two instances where this is not the case: a uniform grid with periodic repetition and a grid with points at the zeros of the Chebyshev polynomials, ![]() , or Chebyshev–Gauss–Lobatto points [F96a], [QV94]. The computation in both of these cases can be done using a fast Fourier transform, which is efficient and minimizes roundoff error.
, or Chebyshev–Gauss–Lobatto points [F96a], [QV94]. The computation in both of these cases can be done using a fast Fourier transform, which is efficient and minimizes roundoff error.
| "DifferenceOrder"->n | use n th-order finite differences to approximate the derivative |
| "DifferenceOrder"->Length[grid] | use the highest possible order finite differences to approximate the derivative on the grid (not generally recommended) |
| "DifferenceOrder"->"Pseudospectral" | use a pseudospectral derivative approximation; only applicable when the grid points are spaced corresponding to the Chebyshev–Gauss–Lobatto points or when the grid is uniform with PeriodicInterpolation->True |
| "DifferenceOrder"->{n1,n2,…} | use difference orders n1, n2, … in dimensions 1, 2, …, respectively |
Settings for the "DifferenceOrder" option.
The Chebyshev–Gauss–Lobatto points are the zeros of ![]() . Using the property
. Using the property ![]() , these can be shown to be at
, these can be shown to be at ![]() .
.
Even though the approximation is somewhat better in the center (because the points are more closely spaced there in the uniform grid), the plot clearly shows the disastrous oscillation typical of overly high-order finite difference approximations. Using the Chebyshev–Gauss–Lobatto spacing has minimized this.
With the assumption of periodicity, the approximation is significantly improved. The accuracy of the periodic pseudospectral approximations is sufficiently high to justify, in some cases, using a larger computational domain to simulate periodicity, say for a pulse like the example. Despite the great accuracy of these approximations, they are not without pitfalls: one of the worst is probably aliasing error, whereby an oscillatory function component with too great a frequency can be misapproximated or disappear entirely.
Accuracy and Convergence of Finite Difference Approximations
When using finite differences, it is important to keep in mind that the truncation error, or the asymptotic approximation error induced by cutting off the Taylor series approximation, is not the only source of error. There are two other sources of error in applying finite difference formulas; condition error and roundoff error [GMW81]. Roundoff error comes from roundoff in the arithmetic computations required. Condition error comes from magnification of any errors in the function values, typically from the division by a power of the step size, and so grows with decreasing step size. This means that in practice, even though the truncation error approaches zero as ![]() does, the actual error will start growing beyond some point. The following figures demonstrate the typical behavior as
does, the actual error will start growing beyond some point. The following figures demonstrate the typical behavior as ![]() becomes small for a smooth function.
becomes small for a smooth function.
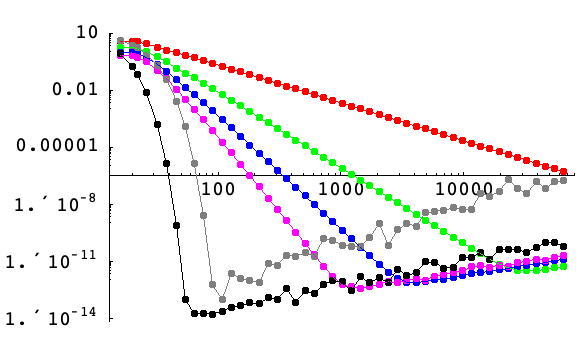
Here is a logarithmic plot of the maximum error for approximating the first derivative of the Gaussian ![]() at points on a grid covering the interval
at points on a grid covering the interval ![]() as a function of the number of grid points,
as a function of the number of grid points, ![]() , using machine precision. Finite differences of order 2, 4, 6, and 8 on a uniform grid are shown in red, green, blue, and magenta, respectively. Pseudospectral derivatives with uniform (periodic) and Chebyshev spacing are shown in black and gray, respectively.
, using machine precision. Finite differences of order 2, 4, 6, and 8 on a uniform grid are shown in red, green, blue, and magenta, respectively. Pseudospectral derivatives with uniform (periodic) and Chebyshev spacing are shown in black and gray, respectively.
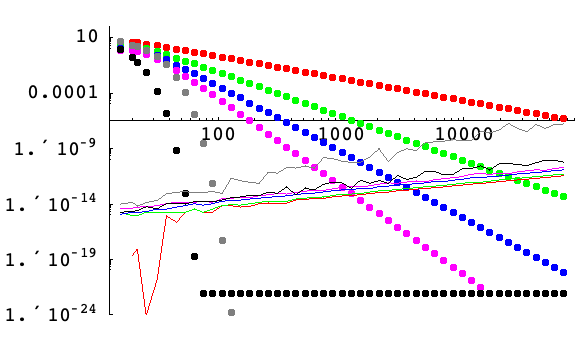
Here is a logarithmic plot of the truncation error (dotted) and the condition and roundoff error (solid line) for approximating the first derivative of the Gaussian ![]() at points on a grid covering the interval
at points on a grid covering the interval ![]() as a function of the number of grid points,
as a function of the number of grid points, ![]() . Finite differences of order 2, 4, 6, and 8 on a uniform grid are shown in red, green, blue, and magenta, respectively. Pseudospectral derivatives with uniform (periodic) and Chebyshev spacing are shown in black and gray, respectively. The truncation error was computed by computing the approximations with very high precision. The roundoff and condition error was estimated by subtracting the machine-precision approximation from the high-precision approximation. The roundoff and condition error tends to increase linearly (because of the
. Finite differences of order 2, 4, 6, and 8 on a uniform grid are shown in red, green, blue, and magenta, respectively. Pseudospectral derivatives with uniform (periodic) and Chebyshev spacing are shown in black and gray, respectively. The truncation error was computed by computing the approximations with very high precision. The roundoff and condition error was estimated by subtracting the machine-precision approximation from the high-precision approximation. The roundoff and condition error tends to increase linearly (because of the ![]() factor common to finite difference formulas for the first derivative) and tends to be a little bit higher for higher-order derivatives. The pseudospectral derivatives show more variations because the error of the FFT computations varies with length. Note that the truncation error for the uniform (periodic) pseudospectral derivative does not decrease below about
factor common to finite difference formulas for the first derivative) and tends to be a little bit higher for higher-order derivatives. The pseudospectral derivatives show more variations because the error of the FFT computations varies with length. Note that the truncation error for the uniform (periodic) pseudospectral derivative does not decrease below about ![]() . This is because, mathematically, the Gaussian is not a periodic function; this error, in essence, gives the deviation from periodicity.
. This is because, mathematically, the Gaussian is not a periodic function; this error, in essence, gives the deviation from periodicity.
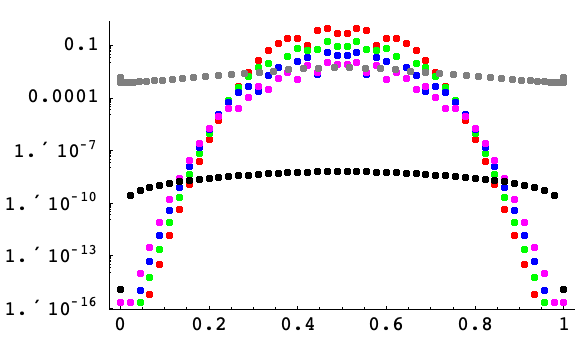
A semilogarithmic plot of the error for approximating the first derivative of the Gaussian ![]() as a function of
as a function of ![]() at points on a 45-point grid covering the interval
at points on a 45-point grid covering the interval ![]() . Finite differences of order 2, 4, 6, and 8 on a uniform grid are shown in red, green, blue, and magenta, respectively. Pseudospectral derivatives with uniform (periodic) and Chebyshev spacing are shown in black and gray, respectively. All but the pseudospectral derivative with Chebyshev spacing were computed using uniform spacing
. Finite differences of order 2, 4, 6, and 8 on a uniform grid are shown in red, green, blue, and magenta, respectively. Pseudospectral derivatives with uniform (periodic) and Chebyshev spacing are shown in black and gray, respectively. All but the pseudospectral derivative with Chebyshev spacing were computed using uniform spacing ![]() . It is apparent that the error for the pseudospectral derivatives is not so localized; not surprising since the approximation at any point is based on the values over the whole grid. The errors for the finite difference approximations are localized and the magnitude of the errors follows the size of the Gaussian (which is parabolic on a semilogarithmic plot).
. It is apparent that the error for the pseudospectral derivatives is not so localized; not surprising since the approximation at any point is based on the values over the whole grid. The errors for the finite difference approximations are localized and the magnitude of the errors follows the size of the Gaussian (which is parabolic on a semilogarithmic plot).
From the second plot, it is apparent that there is a size for which the best possible derivative approximation is found; for larger ![]() , the truncation error dominates, and for smaller
, the truncation error dominates, and for smaller ![]() , the condition and roundoff error dominate. The optimal
, the condition and roundoff error dominate. The optimal ![]() tends to give better approximations for higher-order differences. This is not typically an issue for spatial discretization of PDEs because computing to that level of accuracy would be prohibitively expensive. However, this error balance is a vitally important issue when using low-order differences to approximate, for example, Jacobian matrices. To avoid extra function evaluations, first-order forward differences are usually used, and the error balance is proportional to the square root of unit roundoff, so picking a good value of
tends to give better approximations for higher-order differences. This is not typically an issue for spatial discretization of PDEs because computing to that level of accuracy would be prohibitively expensive. However, this error balance is a vitally important issue when using low-order differences to approximate, for example, Jacobian matrices. To avoid extra function evaluations, first-order forward differences are usually used, and the error balance is proportional to the square root of unit roundoff, so picking a good value of ![]() is important [GMW81].
is important [GMW81].
The plots show the situation typical for smooth functions where there are no real boundary effects. If the parameter in the Gaussian is changed so the function is flatter, boundary effects begin to appear.
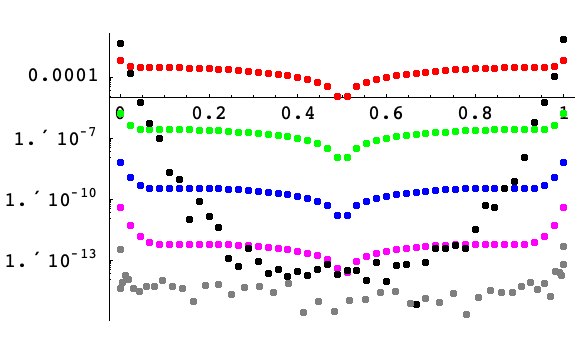
A semilogarithmic plot of the error for approximating the first derivative of the Gaussian ![]() as a function of
as a function of ![]() at points on a 45-point grid covering the interval
at points on a 45-point grid covering the interval ![]() . Finite differences of order 2, 4, 6, and 8 on a uniform grid are shown in red, green, blue, and magenta, respectively. Pseudospectral derivatives with uniform (nonperiodic) and Chebyshev spacing are shown in black and gray, respectively. All but the pseudospectral derivative with Chebyshev spacing were computed using uniform spacing
. Finite differences of order 2, 4, 6, and 8 on a uniform grid are shown in red, green, blue, and magenta, respectively. Pseudospectral derivatives with uniform (nonperiodic) and Chebyshev spacing are shown in black and gray, respectively. All but the pseudospectral derivative with Chebyshev spacing were computed using uniform spacing ![]() . The errors for the finite difference approximations are localized, and the magnitude of the errors follows the magnitude of the first derivative of the Gaussian. The error near the boundary for the uniform spacing pseudospectral (order-45 polynomial) approximation becomes enormous; as
. The errors for the finite difference approximations are localized, and the magnitude of the errors follows the magnitude of the first derivative of the Gaussian. The error near the boundary for the uniform spacing pseudospectral (order-45 polynomial) approximation becomes enormous; as ![]() decreases, this is not bounded. On the other hand, the error for the Chebyshev spacing pseudospectral is more uniform and overall quite small.
decreases, this is not bounded. On the other hand, the error for the Chebyshev spacing pseudospectral is more uniform and overall quite small.
From what has so far been shown, it would appear that the higher the order of the approximation, the better. However, there are two additional issues to consider. The higher-order approximations lead to more expensive function evaluations, and if implicit iteration is needed (as for a stiff problem), then not only is computing the Jacobian more expensive, but the eigenvalues of the matrix also tend to be larger, leading to more stiffness and more difficulty for iterative solvers. This is at an extreme for pseudospectral methods, where the Jacobian has essentially no nonzero entries [F96a]. Of course, these problems are a trade-off for smaller system (and hence matrix) size.
The other issue is associated with discontinuities. Typically, the higher-order the polynomial approximation, the worse the approximation. To make matters even worse, for a true discontinuity, the errors magnify as the grid spacing is reduced.
A plot of approximations for the first derivative of the discontinuous unit step function f(x)=UnitStep(x - 1/2) as a function of ![]() at points on a 128-point grid covering the interval
at points on a 128-point grid covering the interval ![]() . Finite differences of order 2, 4, 6, and 8 on a uniform grid are shown in red, green, blue, and magenta, respectively. Pseudospectral derivatives with uniform (periodic) and Chebyshev spacing are shown in black and gray, respectively. All but the pseudospectral derivative with Chebyshev spacing were computed using uniform spacing
. Finite differences of order 2, 4, 6, and 8 on a uniform grid are shown in red, green, blue, and magenta, respectively. Pseudospectral derivatives with uniform (periodic) and Chebyshev spacing are shown in black and gray, respectively. All but the pseudospectral derivative with Chebyshev spacing were computed using uniform spacing ![]() . All show oscillatory behavior, but it is apparent that the Chebyshev pseudospectral derivative does better in this regard.
. All show oscillatory behavior, but it is apparent that the Chebyshev pseudospectral derivative does better in this regard.
There are numerous alternatives that are used around known discontinuities, such as front tracking. First-order forward differences minimize oscillation, but introduce artificial viscosity terms. One good alternative is the so-called essentially nonoscillatory (ENO) schemes, which have full order away from discontinuities but introduce limits near discontinuities that limit the approximation order and the oscillatory behavior. At this time, ENO schemes are not implemented in NDSolve.
In summary, choosing an appropriate difference order depends greatly on the problem structure. The default of 4 was chosen to be generally reasonable for a wide variety of PDEs, but you may want to try other settings for a particular problem to get better results.
Differentiation Matrices
Since differentiation, as well as naturally finite difference approximation, is a linear operation, an alternative way of expressing the action of a FiniteDifferenceDerivativeFunction is with a matrix. A matrix that represents an approximation to the differential operator is referred to as a differentiation matrix [F96a]. While differentiation matrices may not always be the optimal way of applying finite difference approximations (particularly in cases where an FFT can be used to reduce complexity and error), they are invaluable as aids for analysis and, sometimes, for use in the linear solvers often needed to solve PDEs.
Let FDDF represent an NDSolve`FiniteDifferenceDerivativeFunction[data] object.
| FDDF@"DifferentiationMatrix" | recast the linear operation of FDDF as a matrix that represents the linear operator |
Forming a differentiation matrix.
The matrix is given in a sparse form because, in general, differentiation matrices have relatively few nonzero entries.
As mentioned previously, the matrix form is useful for analysis. For example, it can be used in a direct solver or to find the eigenvalues that could, for example, be used for linear stability analysis.
For pseudospectral derivatives, which can be computed using fast Fourier transforms, it may be faster to use the differentiation matrix for small size, but ultimately, on a larger grid, the better complexity and numerical properties of the FFT make this the much better choice.
For multidimensional derivatives, the matrix is formed so that it is operating on the flattened data, the KroneckerProduct of the matrices for the one-dimensional derivatives. It is easiest to understand this through an example.
Note that the differentiation matrix is a 1353×1353 matrix. The number 1353 is the total number of points on the tensor product grid; that, of course, is the product of the number of points on the ![]() and
and ![]() grids. The differentiation matrix operates on a vector of data that comes from flattening data on the tensor product grid. The matrix is also very sparse; only about one-half of a percent of the entries are nonzero. This is easily seen with a plot of the positions with nonzero values.
grids. The differentiation matrix operates on a vector of data that comes from flattening data on the tensor product grid. The matrix is also very sparse; only about one-half of a percent of the entries are nonzero. This is easily seen with a plot of the positions with nonzero values.
The matrix is the KroneckerProduct, or direct matrix product of the one-dimensional matrices.
Using the differentiation matrix results in slightly different values for machine numbers because the order of operations is different, which in turn leads to different roundoff errors.
The differentiation matrix can be advantageous when what is desired is a linear combination of derivatives. For example, the computation of the Laplacian operator can be put into a single matrix.
Interpretation of Discretized Dependent Variables
When a dependent variable is given in WhenEvent, in a monitor (e.g. StepMonitor) option or in a method where interpretation of the dependent variable is needed (e.g. Projection), for ODEs, the interpretation is generally clear: at a particular value of time (or the independent variable), use the value for that component of the solution for the dependent variable.
For PDEs, the interpretation to use is not so obvious. Mathematically speaking, the dependent variable at a particular time is a function of space. This leads to the default interpretation, which is to represent the dependent variable as an approximate function across the spatial domain using an InterpolatingFunction.
Another possible interpretation for PDEs is to consider the dependent variable at a particular time as representing the spatially discretized values at that time—that is, discretized both in time and space. You can request that monitors and methods use this fully discretized interpretation by using the MethodOfLines option DiscretizedMonitorVariables->True.
The best way to see the difference between the two interpretations is with an example.
In executing the command above, u[t,x] in the StepMonitor is effectively a function of x, so it can be plotted with Plot. You could do other operations on it, such as numerical integration.
In this case, u[t,x] is given at each step as a vector with the discretized values of the solution on the spatial grid. Showing the discretization points makes for a more informative monitor in this example since it allows you to see how well the front is resolved as it forms.
The vector of values contains no information about the grid itself; in the example, the plot is made versus the index values, which shows the correct spacing for a uniform grid. Note that when u is interpreted as a function, the grid will be contained in the InterpolatingFunction used to represent the spatial solution, so if you need the grid, the easiest way to get it is to extract it from the InterpolatingFunction, which represents u[t,x].
Finally note that using the discretized representation is significantly faster. This may be an important issue if you are using the representation in WhenEvent or solution methods such as Projection. An example where event detection is used to prevent solutions from going beyond a computational domain is computed much more quickly by using the discretized interpretation.
Boundary Conditions
Often, with PDEs, it is possible to determine a good numerical way to apply boundary conditions for a particular equation and boundary condition. The example given previously in the introduction of "The Numerical Method of Lines" is such a case. However, the problem of finding a general algorithm is much more difficult and is complicated somewhat by the effect that boundary conditions can have on stiffness and overall stability.
Periodic boundary conditions are particularly simple to deal with: periodic interpolation is used for the finite differences. Since pseudospectral approximations are accurate with uniform grids, solutions can often be found quite efficiently.
| NDSolve[{eqn1,eqn2,…,u1[t,xmin]==u1[t,xmax],u2[t,xmin]==u2[t,xmax],…},{u1[t,x],u2[t,x],…},{t,tmin,tmax},{x,xmin,xmax}] | |
| solve a system of partial differential equations for function u1, u2, … with periodic boundary conditions in the spatial variable x (assuming that t is a temporal variable) | |
| NDSolve[{eqn1,eqn2,…,u1[t,x1min,x2,…]==u1[t,x1max x2,…],u2[t,x1min,x2,…]==u2[t,x1max x2,…],…},{u1[t,x1,x2,…],u2[t,x1,x2,…],…}, {t,tmin,tmax},{x,xmin,xmax}] | |
| solve a system of partial differential equations for function u1, u2, … with periodic boundary conditions in the spatial variable x1 (assuming that t is a temporal variable) | |
Giving boundary conditions for partial differential equations.
If you are solving for several functions u1, u2, …, then for any of the functions to have periodic boundary conditions, all of them must (the condition need only be specified for one function). If working with more than one spatial dimension, you can have periodic boundary conditions in some independent variable dimensions and not in others.
In the InterpolatingFunction object returned as a solution, the ellipses in the notation {…,xmin,xmax,…} are used to indicate that this dimension repeats periodically.
NDSolve uses two methods for nonperiodic boundary conditions. Both have their merits and drawbacks. The first method is to differentiate the boundary conditions with respect to the temporal variable and solve for the resulting differential equation(s) at the boundary. The second method is to discretize each boundary condition as it is. This typically results in an algebraic equation for the boundary solution component, so the equations must be solved with a DAE solver. This is controlled with the DifferentiateBoundaryConditions option to MethodOfLines.
To see how the differentiation method works, consider again the simple example of the method of lines introduction section. In the first formulation, the Dirichlet boundary condition at ![]() was handled by differentiation with respect to
was handled by differentiation with respect to ![]() . The Neumann boundary condition was handled using the idea of reflection, which worked fine for a second-order finite difference approximation but does not generalize quite as easily to higher order (though it can be done easily for this problem by computing the entire reflection). The differentiation method, however, can be used for any-order differences on the Neumann boundary condition at
. The Neumann boundary condition was handled using the idea of reflection, which worked fine for a second-order finite difference approximation but does not generalize quite as easily to higher order (though it can be done easily for this problem by computing the entire reflection). The differentiation method, however, can be used for any-order differences on the Neumann boundary condition at ![]() . As an example, a solution to the problem will be developed using fourth-order differences.
. As an example, a solution to the problem will be developed using fourth-order differences.
The advantage of this equation is that by including the derivative you will explicitly have u0'[t], which you need to solve for in order to handle the discretized system as a set of ODEs. By adding in the discretized boundary condition, the solution of this equation alone converges asymptotically to the correct boundary condition, even when there are temporary deviations or the initial condition is inconsistent. This can be seen from its exact solution.
Note that the value of the scaling factor will determine the rate of convergence for this solution of the actual boundary condition. This factor can be controlled in NDSolve using the option setting "DifferentiateBoundaryConditions"->{True,"ScaleFactor"->sf}. With the default "ScaleFactor" value of Automatic, a scaling factor of 1 is used for Dirichlet boundary conditions and a scaling factor of 0 is used otherwise.
Technically, it is not necessary that the discretization of the boundary condition be done with the same difference order as the rest of the DE; in fact, since the error terms for the one-sided derivatives are much larger, it may sometimes be desirable to increase the order near the boundaries. NDSolve does not do this because it is desirable that the difference order and the InterpolatingFunction interpolation order be consistent across the spatial direction.
Treating the boundary conditions as algebraic conditions saves a couple of steps in the processing at the expense of using a DAE solver.
For this example, the boundary condition was satisfied well within tolerances in both cases, but the differentiation method did very slightly better. This is not always true; when the boundary condition is differentiated, there may be some local drift of the solution away from the actual boundary condition.
When using NDSolve, it is easy to switch between the two methods by using the DifferentiateBoundaryConditions option. Remember that when you use DifferentiateBoundaryConditions->False, you are not as free to choose integration methods; the method needs to be a DAE solver.
With systems of PDEs or equations with higher-order derivatives having more complicated boundary conditions, both methods can be made to work in general. When there are multiple boundary conditions at one end, it may be necessary to attach some conditions to interior points. Here is an example of a PDE with two boundary conditions at each end of the spatial interval.
Understanding the message about spatial error will be addressed in the next section. For now, ignore the message and consider the boundary conditions.
It is clear that the boundary conditions are satisfied to well within the tolerances allowed by AccuracyGoal and PrecisionGoal options. It is typical that conditions with higher-order derivatives will not be satisfied as well as those with lower-order derivatives.
There are two reasons that the scaling factor to multiply the original boundary condition is zero for boundary conditions with spatial derivatives. First, imposing the condition for the discretized equation is only a spatial approximation, so it does not always make sense to enforce it as exactly as possible for all time. Second, particularly with higher-order spatial derivatives, the large coefficients from one-sided finite differencing can be a potential source of instability when the condition is included. For the example just above, this happens for the boundary condition on ![]() .
.

Inconsistent Boundary Conditions
It is important that the boundary conditions you specify be consistent with both the initial condition and the PDE. If this is not the case, NDSolve will issue a message warning about the inconsistency. When this happens, the solution may not satisfy the boundary conditions, and in the worst cases, instability may appear.
The reason the boundary condition is not satisfied is because the integration of the ODEs begins with the given initial conditions. The differentiated equation at the boundary, once it is differentiated, becomes ![]() , so the solution is approaching the correct boundary condition but does not get very close in the integration interval.
, so the solution is approaching the correct boundary condition but does not get very close in the integration interval.
It is not always the case that the DAE solver will be able find consistent initial conditions that lead to an effectively correct solution like this. One way of improving the solution with the ODE method is to use a higher value of the boundary condition scaling factor in "DifferentiateBoundaryConditions"->{True,"ScaleFactor"->sf} than the default of 1.
When the scale factor is large, the equations may be more difficult for the solvers to integrate since it introduces a possible source of stiffness. You can see from the solution with scaling factor 100 that there is a rapidly varying initial transient.
A more certain way to handle this problem is to give an initial condition that is consistent with the boundary conditions, even if it is discontinuous. In this case the unit step function does what is needed.
In general, with discontinuous initial conditions, spatial error estimates cannot be satisfied. Since they are predicated on smoothness, in general, it is best to choose how well you want to model the effect of the discontinuity by either giving a smooth function that approximates the discontinuity or by specifying explicitly the number of points to use in the spatial discretization. More detail on spatial error estimates and discretization is given in "Spatial Error Estimates".
A more subtle inconsistency arises when the temporal variable has higher-order derivatives and boundary conditions may be differentiated more than once.
The initial condition ![]() satisfies the boundary conditions, so you might be surprised that NDSolve issues the NDSolve::ibcinc message.
satisfies the boundary conditions, so you might be surprised that NDSolve issues the NDSolve::ibcinc message.
The inconsistency appears when you differentiate the second initial condition with respect to ![]() , giving
, giving ![]() , and differentiate the second boundary condition with respect to
, and differentiate the second boundary condition with respect to ![]() , giving
, giving ![]() . These two are inconsistent at
. These two are inconsistent at ![]() .
.
Occasionally, NDSolve will issue the NDSolve::ibcinc message warning about inconsistent boundary conditions when they are actually consistent. This happens due to discretization error in approximating Neumann boundary conditions or any boundary condition that involves a spatial derivative. The reason this happens is that spatial error estimates (see "Spatial Error Estimates") used to determine how many points to discretize with are based on the PDE and the initial condition, but not the boundary conditions. The one-sided finite difference formulas that are used to approximate the boundary conditions also have larger error than a centered formula of the same order, leading to additional discretization error at the boundary. Typically this is not a problem, but it is possible to construct examples where it does occur.
When the boundary conditions are consistent, a way to correct this error is to specify that NDSolve use a finer spatial discretization.
Spatial Error Estimates
Overview
When NDSolve solves a PDE, unless you have specified the spatial grid for it to use, by giving it explicitly or by giving equal values for the MinPoints and MaxPoints options, NDSolve needs to make a spatial error estimate.
Ideally, the spatial error estimates would be monitored over time and the spatial mesh updated according to the evolution of the solution. The problem of grid adaptivity is difficult enough for a specific type of PDE and certainly has not been solved in any general way. Furthermore, techniques such as local refinement can be problematic with the method of lines since changing the number of mesh points requires a complete restart of the ODE methods. There are moving mesh techniques that appear promising for this approach, but at this point, NDSolve uses a static grid. The grid to use is determined by an a priori error estimate based on the initial condition. An a posteriori check is done at the end of the temporal interval for reasonable consistency and a warning message is given if that fails. This can, of course, be fooled, but in practice it provides a reasonable compromise. The most common cause of failure is when initial conditions have little variation, so the estimates are essentially meaningless. In this case, you may need to choose some appropriate grid settings yourself.
A Priori Error Estimates
When NDSolve solves a PDE using the method of lines, a decision has to be made on an appropriate spatial grid. NDSolve does this using an error estimate based on the initial condition (thus, a priori).
It is easiest to show how this works in the context of an example. For illustrative purposes, consider the sine-Gordon equation in one dimension with periodic boundary conditions.
The temporal points are chosen adaptively by the ODE method based on local error control. NDSolve used 97 (98 including the periodic endpoint) spatial points. This choice will be illustrated through the steps that follow.
In the equation-processing phase of NDSolve, one of the first things that happens is that equations with second-order (or higher) temporal derivatives are replaced with systems with only first-order temporal derivatives.
The next stage is to solve for the temporal derivatives.
Now the problem is to choose a uniform grid that will approximate the derivative to within local error tolerances as specified by AccuracyGoal and PrecisionGoal. For this illustration, use the default "DifferenceOrder" (4) and the default AccuracyGoal and PrecisionGoal (both 4 for PDEs). The methods used to integrate the system of ODEs that results from discretization base their own error estimates on the assumption of sufficiently accurate function values. The estimates here have the goal of finding a spatial grid for which (at least with the initial condition) the spatial error is somewhat balanced with the local temporal error.
The error estimate is based on Richardson extrapolation. If you know that the error is ![]() and you have two approximations,
and you have two approximations, ![]() and
and ![]() , at different values,
, at different values, ![]() and
and ![]() of
of ![]() , then you can, in effect, extrapolate to the limit
, then you can, in effect, extrapolate to the limit ![]() to get an error estimate
to get an error estimate
so the error in ![]() is estimated to be
is estimated to be
Here ![]() and
and ![]() are vectors of different length and
are vectors of different length and ![]() is a function, so you need to choose an appropriate norm. If you choose
is a function, so you need to choose an appropriate norm. If you choose ![]() , then you can simply use a scaled norm on the components common to both vectors, which is all of
, then you can simply use a scaled norm on the components common to both vectors, which is all of ![]() and every other point of
and every other point of ![]() . This is a good choice because it does not require any interpolation between grids.
. This is a good choice because it does not require any interpolation between grids.
For a given interval on which you want to set up a uniform grid, you can define a function ![]() , where
, where ![]() is the length of the interval such that the grid is
is the length of the interval such that the grid is ![]() , where
, where ![]() .
.
For a given grid, the equation can be discretized using finite differences. This is easily done using NDSolve`FiniteDifferenceDerivative.
For a given step size and grid, you can also discretize the initial conditions for ![]() and
and ![]() .
.
The quantity of interest is the approximation of the right-hand side for a particular value of ![]() with this initial condition.
with this initial condition.
Starting with a particular value of ![]() , you can obtain the error estimate by generating the right-hand side for
, you can obtain the error estimate by generating the right-hand side for ![]() and
and ![]() points.
points.
As mentioned earlier, every other point on the grid with ![]() points lies on the grid with
points lies on the grid with ![]() points. Thus, for simplicity, you can use a norm that only compares points common to both grids. Because the goal is to ultimately satisfy absolute and relative tolerance criteria, it is appropriate to use a scaled norm. In addition to taking into account the size of the right-hand side for the scaling, it is also important to include the size of the corresponding components of
points. Thus, for simplicity, you can use a norm that only compares points common to both grids. Because the goal is to ultimately satisfy absolute and relative tolerance criteria, it is appropriate to use a scaled norm. In addition to taking into account the size of the right-hand side for the scaling, it is also important to include the size of the corresponding components of ![]() and
and ![]() on the grid since error in the right-hand side is ultimately included in
on the grid since error in the right-hand side is ultimately included in ![]() and
and ![]() .
.
To get the error estimate from the distance, according to the Richardson extrapolation formula (3), this simply needs to be divided by ![]() .
.
The goal is to find the minimum value of ![]() , such that the error estimate is less than or equal to 1 (since it is based on a scaled norm). In principle, it would be possible to use a root-finding algorithm on this, but since
, such that the error estimate is less than or equal to 1 (since it is based on a scaled norm). In principle, it would be possible to use a root-finding algorithm on this, but since ![]() can only be an integer, this would be overkill and adjustments would have to be made to the stopping conditions. An easier solution is simply to use the Richardson extrapolation formula to predict what value of
can only be an integer, this would be overkill and adjustments would have to be made to the stopping conditions. An easier solution is simply to use the Richardson extrapolation formula to predict what value of ![]() would be appropriate and repeat the prediction process until the appropriate
would be appropriate and repeat the prediction process until the appropriate ![]() is found.
is found.
or in terms of ![]() , which is proportional to the reciprocal of
, which is proportional to the reciprocal of ![]() ,
,
It is often the case that a prediction based on a very coarse grid will be inadequate. A coarse grid may completely miss some solution features that contribute to the error on a finer grid. Also, the error estimate is based on an asymptotic formula, so for coarse spacings, the estimate itself may not be very good, even when all the solution features are resolved to some extent.
In practice, it can be fairly expensive to compute these error estimates. Also, it is not necessary to find the very optimal ![]() , but one that satisfies the error estimate. Remember, everything can change as the PDE evolves, so it is simply not worth a lot of extra effort to find an optimal spacing for just the initial time. A simple solution is to include an extra factor greater than 1 in the prediction formula for the new
, but one that satisfies the error estimate. Remember, everything can change as the PDE evolves, so it is simply not worth a lot of extra effort to find an optimal spacing for just the initial time. A simple solution is to include an extra factor greater than 1 in the prediction formula for the new ![]() . Even with an extra factor, it may still take a few iterations to get to an acceptable value. It does, however, typically make the process faster.
. Even with an extra factor, it may still take a few iterations to get to an acceptable value. It does, however, typically make the process faster.
It is important to note that this process must have a limiting value since it may not be possible to satisfy the error tolerances, for example, with a discontinuous initial function. In NDSolve, the MaxSteps option provides the limit; for spatial discretization, this defaults to a total of 10000 across all spatial dimensions.
Pseudospectral derivatives cannot use this error estimate since they have an exponential rather than a polynomial convergence. An estimate can be made based on the formula used earlier in the limit p->Infinity. What this amounts to is considering the result on the finer grid to be exact and basing the error estimate on the difference since ![]() approaches
approaches ![]() . A better approach is to use the fact that on a given grid with
. A better approach is to use the fact that on a given grid with ![]() points the pseudospectral method is
points the pseudospectral method is ![]() . When comparing for two grids, it is appropriate to use the smaller
. When comparing for two grids, it is appropriate to use the smaller ![]() for
for ![]() . This provides an imperfect, but adequate, estimate for the purpose of determining grid size.
. This provides an imperfect, but adequate, estimate for the purpose of determining grid size.
The prediction formula can be modified to use ![]() instead of
instead of ![]() in a similar way.
in a similar way.
When finalizing the choice of ![]() for a pseudospectral method, an additional consideration is to choose a value that not only satisfies the tolerance conditions, but is also an efficient length for computing FFTs. In the Wolfram Language, an efficient FFT does not require a power of two length since the Fourier command has a prime factor algorithm built in.
for a pseudospectral method, an additional consideration is to choose a value that not only satisfies the tolerance conditions, but is also an efficient length for computing FFTs. In the Wolfram Language, an efficient FFT does not require a power of two length since the Fourier command has a prime factor algorithm built in.
Typically, the difference order has a profound effect on the number of points required to satisfy the error estimate.
A table of the number of points required as a function of the difference order goes a long way toward explaining why the default setting for the method of lines is "DifferenceOrder"->4. The improvement from 2 to 4 is usually most dramatic and in the default tolerance range, fourth-order differences do not tend to produce large roundoff errors, which can be the case with higher orders. Pseudospectral differences are often a good choice, particularly with periodic boundary conditions, but they are not a good choice for the default because they lead to full Jacobian matrices, which can be expensive to generate and solve if needed for stiff equations.
For nonperiodic grids, the error estimate is done using only interior points. The reason is that the error coefficients for the derivatives near the boundary are different. This may miss features that are near the boundary, but the main idea is to keep the estimate simple and inexpensive since the evolution of the PDE may change everything anyway.
For multiple spatial dimensions, the determination is made one dimension at a time. Since better resolution in one dimension may change the requirements for another, the process is repeated in reverse order to improve the choice.
A Posteriori Error Estimates
When the solution of a PDE is computed with NDSolve, a final step is to do a spatial error estimate on the evolved solution and issue a warning message if this is excessively large.
These error estimates are done in a manner similar to the a priori estimates described previously. The only real difference is that, instead of using grids with ![]() and
and ![]() points to estimate the error, grids with
points to estimate the error, grids with ![]() and
and ![]() points are used. This is because, while there is no way to generate the values on a grid of
points are used. This is because, while there is no way to generate the values on a grid of ![]() points without using interpolation, which would introduce its own errors, values are readily available on a grid of
points without using interpolation, which would introduce its own errors, values are readily available on a grid of ![]() points simply by taking every other value. This is easily done in the Richardson extrapolation formula by using
points simply by taking every other value. This is easily done in the Richardson extrapolation formula by using ![]() , which gives
, which gives
The large amount of local variation seen in this function is typical. (In this example, the large peak occurs right at the time the original single peak is splitting into separate waves.) For that reason, NDSolve does not warn about excessive error unless this estimate gets above 10 (rather than the value of 1, which is used to choose the grid based on initial conditions). The extra factor of 10 is further justified by the fact that the a posteriori error estimate is less accurate than the a priori one. Thus, when NDSolve issues a warning message based on the a posteriori error estimate, it is usually because new solution features have appeared or because there is instability in the solution process.

When the NDSolve::eerr message does show up, it may be necessary for you to use options to control the grid selection process since it is likely that the default settings did not find an accurate solution.
Controlling the Spatial Grid Selection
The NDSolve implementation of the method of lines has several ways to control the selection of the spatial grid.
option name | default value | |
| AccuracyGoal | Automatic | the number of digits of absolute tolerance for determining grid spacing |
| PrecisionGoal | Automatic | the number of digits of relative tolerance for determining grid spacing |
| "DifferenceOrder" | Automatic | the order of finite difference approximation to use for spatial discretization |
| Coordinates | Automatic | the list of coordinates for each spatial dimension |
| MinPoints | Automatic | the minimum number of points to be used for each dimension in the grid; for Automatic, value will be determined by the minimum number of points needed to compute an error estimate for the given difference order |
| MaxPoints | Automatic | the maximum number of points to be used in the grid |
| StartingPoints | Automatic | the number of points to begin the process of grid refinement using the a priori error estimates |
| MinStepSize | Automatic | the minimum grid spacing to use |
| MaxStepSize | Automatic | the maximum grid spacing to use |
| StartingStepSize | Automatic | the grid spacing to use to begin the process of grid refinement using the a priori error estimates |
Tensor product grid options for the method of lines.
All the options for tensor product grid discretization can be given as a list with length equal to the number of spatial dimensions, in which case the parameter for each spatial dimension is determined by the corresponding component of the list.
With the exception of pseudospectral methods on nonperiodic problems, discretization is done with uniform grids, so when solving a problem on interval length ![]() , there is a direct correspondence between the Points and StepSize options.
, there is a direct correspondence between the Points and StepSize options.
The StepSize options are effectively converted to the equivalent Points values. They are simply provided for convenience since sometimes it is more natural to relate problem specification to step size rather than the number of discretization points. When values other than Automatic are specified for both the Points and corresponding StepSize option, generally, the more stringent restriction is used.
In the previous section an example was shown where the solution was not resolved sufficiently because the solution steepened as it evolved. The examples that follow will show some different ways of modifying the grid parameters so that the near shock is better resolved.
One way to avoid the oscillations that showed up in the solution as the profile steepened is to make sure that you use sufficient points to resolve the profile at its steepest. In the one-hump solution of Burgers's equation,
it can be shown [W76] that the width of the shock profile is proportional to ![]() as
as ![]() . More than 95% of the change is included in a layer of width
. More than 95% of the change is included in a layer of width ![]() . Thus, if you pick a maximum step size of half the profile width, there will always be a point somewhere in the steep part of the profile, and there is a hope of resolving it without significant oscillation.
. Thus, if you pick a maximum step size of half the profile width, there will always be a point somewhere in the steep part of the profile, and there is a hope of resolving it without significant oscillation.
Note that resolving the profile alone is by no means sufficient to meet the default tolerances of NDSolve, which requires an accuracy of ![]() . However, once you have sufficient points to resolve the basic profile, it is not unreasonable to project based on the a posteriori error estimate shown in the NDSolve::eerr message (with an extra 10% since, after all, it is just a projection).
. However, once you have sufficient points to resolve the basic profile, it is not unreasonable to project based on the a posteriori error estimate shown in the NDSolve::eerr message (with an extra 10% since, after all, it is just a projection).
To compare solutions like this, it is useful to look at a plot of the solution only at the spatial grid points. Because the grid points are stored as a part of the InterpolatingFunction, it is fairly simple to define a function that does this.
In this example, the left-hand side of the domain really does not need so many points. The points need to be clustered where the steep profile evolves, so it might make sense to consider explicitly specifying a grid that has more points where the profile appears.
Many of the same principles apply to multiple spatial dimensions. Burgers's equation in two dimensions with anisotropy provides a good example.
Similar to the one-dimensional case, the leading edge steepens. Since the viscosity term (![]() ) is larger, the steepening is not quite so extreme, and this default solution actually resolves the front reasonably well. Therefore it should be possible to project from the error estimate to meet the default tolerances. A simple scaling argument indicates that the profile width in the
) is larger, the steepening is not quite so extreme, and this default solution actually resolves the front reasonably well. Therefore it should be possible to project from the error estimate to meet the default tolerances. A simple scaling argument indicates that the profile width in the ![]() direction will be narrower than in the
direction will be narrower than in the ![]() direction by a factor of
direction by a factor of ![]() . Thus, it makes sense that the step sizes in the
. Thus, it makes sense that the step sizes in the ![]() direction can be larger than those in the
direction can be larger than those in the ![]() direction by this factor, or, correspondingly, that the minimum number of points can be a factor of
direction by this factor, or, correspondingly, that the minimum number of points can be a factor of ![]() less.
less.
This solution takes a substantial amount of time to compute, which is not surprising since the solution involves solving a system of more than 18000 ODEs. In many cases, particularly in more than one spatial dimension, the default tolerances may be unrealistic to achieve, so you may have to reduce them by using AccuracyGoal and/or PrecisionGoal appropriately. Sometimes, especially with the coarser grids that come with less stringent tolerances, the systems are not stiff, and it is possible to use explicit methods that avoid the numerical linear algebra, which can be problematic, especially for higher-dimensional problems. For this example, using Method->ExplicitRungeKutta gets the solution in about half the time.
Any of the other grid options can be specified as a list giving the values for each dimension. When only a single value is given, it is used for all the spatial dimensions. The two exceptions to this are MaxPoints, where a single value is taken to be the total number of grid points in the outer product, and Coordinates, where a grid must be specified explicitly for each dimension.
It is important to keep in mind that the a posteriori spatial error estimates are simply estimates of the local error in computing spatial derivatives and may not reflect the actual accumulated spatial error for a given solution. One way to get an estimate of the actual spatial error is to compute the solution to very stringent tolerances in time for different spatial grids. To show how this works, consider again the simpler one-dimensional Burgers's equation.
Given two solutions, a comparison needs to be done between the two. To keep out any sources of error except for that in the solutions themselves, it is best to use the data that is interpolated to make the InterpolatingFunction. This can be done by using points common to the two solutions.
To get an indication of the general trend in error (in cases of instability, solutions do not converge, so this does not assume that), you can compare the difference of successive pairs of solutions.
Here is a logarithmic plot of the maximum spatial error in approximating the solution of Burgers's equation at ![]() as a function of the number of grid points. Finite differences of order 2, 4, and 6 on a uniform grid are shown in red, green, and blue, respectively. Pseudospectral derivatives with uniform (periodic) spacing are shown in black.
as a function of the number of grid points. Finite differences of order 2, 4, and 6 on a uniform grid are shown in red, green, and blue, respectively. Pseudospectral derivatives with uniform (periodic) spacing are shown in black.
In the upper-left part of the plot are the grids where the profile is not adequately resolved, so differences are simply of magnitude order 1 (it would be a lot worse if there was instability). However, once there are a sufficient number of points to resolve the profile without oscillation, convergence becomes quite rapid. Not surprisingly, the slope of the logarithmic line is ![]() , which corresponds to the difference order NDSolve uses by default. If your grid is fine enough to be in the asymptotically converging part, a simpler error estimate could be effected by using the Richardson extrapolation as in the previous two sections, but on the overall solution rather than the local error. On the other hand, computing more values and viewing a plot gives a better indication of whether you are in the asymptotic regime or not.
, which corresponds to the difference order NDSolve uses by default. If your grid is fine enough to be in the asymptotically converging part, a simpler error estimate could be effected by using the Richardson extrapolation as in the previous two sections, but on the overall solution rather than the local error. On the other hand, computing more values and viewing a plot gives a better indication of whether you are in the asymptotic regime or not.
It is fairly clear from the plot that the best solution computed is the pseudospectral one with 2049 points (the one with more points was not computed because its spatial accuracy far exceeds the temporal tolerances that were set). This solution can, in effect, be treated almost as an exact solution, at least up to error tolerances of ![]() or so.
or so.
To get a perspective of how best to solve the problem, it is useful to do the following: for each solution found that was at least a reasonable approximation, recompute it with the temporal accuracy tolerance set to be comparable to the possible spatial accuracy of the solution and plot the resulting accuracy as a function of solution time. The following (somewhat complicated) commands do this.
A logarithmic plot of the error in approximating the solution of Burgers's equation at ![]() as a function of the computation time. Each point shown indicates the number of spatial grid points used to compute the solution. Finite differences of order 2, 4, and 6 on a uniform grid are shown in red, blue, and green, respectively. Pseudospectral derivatives with uniform (periodic) spacing are shown in black. Note that the cost of the pseudospectral method jumps dramatically from 513 to 1025. This is because the method has switched to the stiff solver, which is very expensive with the dense Jacobian produced by the discretization.
as a function of the computation time. Each point shown indicates the number of spatial grid points used to compute the solution. Finite differences of order 2, 4, and 6 on a uniform grid are shown in red, blue, and green, respectively. Pseudospectral derivatives with uniform (periodic) spacing are shown in black. Note that the cost of the pseudospectral method jumps dramatically from 513 to 1025. This is because the method has switched to the stiff solver, which is very expensive with the dense Jacobian produced by the discretization.
The resulting graph demonstrates quite forcefully that, when they work, as in this case, periodic pseudospectral approximations are incredibly efficient. Otherwise, up to a point, the higher the difference order, the better the approximation will generally be. These are all features of smooth problems, which this particular instance of Burgers's equation is. However, the higher-order solutions would generally be quite poor if you went toward the limit ![]() .
.
One final point to note is that the above graph was computed using the Automatic method for the temporal direction. This uses LSODA, which switches between a stiff and nonstiff method depending on how the solution evolves. For the coarser grids, strictly explicit methods are typically a bit faster, and, except for the pseudospectral case, the implicit BDF methods are faster for the finer grids. A variety of alternative ODE methods is available in NDSolve.
Error at the Boundaries
The a priori error estimates are computed in the interior of the computational region because the differences used there all have consistent error terms that can be used to effectively estimate the number of points to use. Including the boundaries in the estimates would complicate the process beyond what is justified for such an a priori estimate. Typically, this approach is successful in keeping the error under reasonable control. However, there are a few cases that can lead to difficulties.
Occasionally it may occur that because the error terms are larger for the one-sided derivatives used at the boundary, NDSolve will detect an inconsistency between boundary and initial conditions, which is an artifact of the discretization error.
The NDSolve::ibcinc message is issued, in this case, completely to the larger discretization error at the right boundary. For this particular example, the extra error is not a problem because it gets damped out due to the nature of the equation. However, it is possible to eliminate the message by using just a few more spatial points.
One other case where error problems at the boundary can affect the discretization unexpectedly is when periodic boundary conditions are given with a function that is not truly periodic, so that an unintended discontinuity is introduced into the computation.
The problem here is that the initial condition is effectively discontinuous when the periodic continuation is taken into account.
Since there is always a large derivative error at the cusps, NDSolve is forced to use the maximum number of points in an attempt to satisfy the a priori error bound. To make matters worse, the extreme change makes solving the resulting ODEs more difficult, leading to a very long solution time that uses a lot of memory.
If the discontinuity is really intended, you will typically want to specify a number of points or spacing for the spatial grid that will be sufficient to handle the aspects of the discontinuity you are interested in. To model discontinuities with high accuracy will typically take specialized methods that are beyond the scope of the general methods that NDSolve provides.
On the other hand, if the discontinuity was unintended, say in this example by simply choosing a computational domain that was too small, it can usually be fixed easily enough by extending the domain or by adding in terms to smooth things between periods.