级数、极限和留数
级数、极限和留数
| Sum[f,{i,imin,imax}] | 和式 |
| Sum[f,{i,imin,imax,di}] | i 按步长 di 增加的和式 |
| Sum[f,{i,imin,imax},{j,jmin,jmax}] | 累次和 |
| Product[f,{i,imin,imax}] | 连乘 |
Wolfram 语言还有多重和与多重积的表示法. Sum[f,{i,imin,imax},{j,jmin,jmax}] 代表关于 i 和 j 的和式,用标准的数学表示法可写为  . 注意,像标准的数学表示法一样,在 Wolfram 语言的表示法中最外层变量的范围首先被给出.
. 注意,像标准的数学表示法一样,在 Wolfram 语言的表示法中最外层变量的范围首先被给出.
在 Sum 和 Product 中指定变量范围的方法是 Wolfram 语言所使用的相当一般的迭代器表示法的一个例子. 在讨论使用 Table 来生成表和列表时("值表的生成")以及在描述 Do 循环时("循环运算")将看到这个表示法.
| {imax} | 重复 imax 次,不带有变量的增加 |
| {i,imax} | i 按步长 1 从 1 增加到 imax |
| {i,imin,imax} | i 按步长 1 从 imin 增加到 imax |
| {i,imin,imax,di} | i 按步长 di 从 imin 增加到 imax |
| {i,imin,imax},{j,jmin,jmax},… | i 从 imin 增加到 imax,对每个这样的值,j 从 jmin 增加到 jmax,等等 |
若给出一个 Wolfram 语言不认识的函数,那么 Series 用导数形式写出其幂级数:
使用 Expand 给出具有 11 项的结果.
| Series[expr,{x,x0,n}] | 求 expr 在 x=x0 处最高到 (x-x0)n 阶项的幂级数展开式 |
| Series[expr,{x,x0,nx},{y,y0,ny}] | |
求先对 y 后对 x 的级数展开式 | |
作为数学术语,Series 可以看作是一种构造函数的泰勒级数的方法.
Series 也能生成某些包含分数和负数幂的幂级数,这是标准泰勒公式所不具有的.
Series 也能处理包含对数的级数:
特别当出现负数幂时,Series 生成的特定幂级数有多少项是一个微妙的问题.
Series 在构造幂级数中遵循的步骤非常类似于 N 在构造实数近似值中遵循的步骤. 二者都从用有限阶或有限精度的近似代替表达式中的最小元素开始,然后计算结果表达式. 如果有消约,这个过程可能给出的最终结果其阶或精度都会小于用户所要求的. 然而,如同 N,Series 有能力重试计算,以使得到的结果具有用户要求的阶. 如果不成功,用户通过指定更高的阶数,仍然可以得到特定阶的结果.
幂级数在 Wolfram 系统中被表示为 SeriesData 对象.
幂级数显示为各项的和,并以 O[x] 的某次幂结尾:
然而,在 Wolfram 系统内部,级数被存贮为 SeriesData 对象:
用户可以根据是否有 O[x] 项来识别以标准形式输出的幂级数. 该项模拟标准数学符号 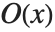 ,表示忽略的
,表示忽略的 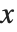 阶项. 考虑到各种一致性因素,Wolfram 系统使用 O[x]^n 表示忽略的
阶项. 考虑到各种一致性因素,Wolfram 系统使用 O[x]^n 表示忽略的 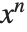 阶项,它对应用于数学符号
阶项,它对应用于数学符号 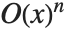 ,而不是较熟悉的
,而不是较熟悉的 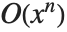 ,虽然二者是等价的.
,虽然二者是等价的.
任何时候如 O[x] 的对象在和式中出现时,Wolfram 系统会实际上将整个和转换成幂级数.
O[x] 的出现使 Wolfram 系统将整个和转换成幂级数:
对数因子在 SeriesData 的系数列单中显式地出现:
| ComposeSeries[series1,series2,…] | 复合幂级数 |
| InverseSeries[series,x] | 反演幂级数 |
| Normal[expr] | 将幂级数转换为普通表达式 |
Normal 截断幂级数,给出普通表达式:
| SeriesCoefficient[series,n] | 给出幂级数 n 次项的系数 |
| LogicalExpand[series1==series2] | 给出由幂级数中相应的系数相等得到的方程 |
| Solve[series1==series2,{a1,a2,…}] | 求解幂级数的系数 |
| Sum[expr,{n,nmin,nmax}] | 求 expr 当 n 从 nmin 到 nmax 的和 |
| RSolve[eqn,a[n],n] | 求解递归方程 |
| RSolve[{eqn1,eqn2,…},{a1[n],a2[n],…},n] | |
求解耦合递归方程组 | |
| RSolve[eqns,a[n1,n2,…],{n1,n2,…}] | |
求解偏递归方程 | |
| Limit[expr,x->x0] | 求 x 趋于 x0 时 expr 的极限 |
并非所有函数在特定的点都有确定的极限. 例如函数 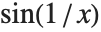 在
在  附近无限振荡,所以在此处无确定极限. 然而只要
附近无限振荡,所以在此处无确定极限. 然而只要 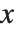 取实数,该函数在
取实数,该函数在  附近的值总是在
附近的值总是在 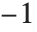 和
和  之间. Limit 使用 Interval 对象表示有界变化的值. 一般地,Interval[{xmin,xmax}] 表示在区间
之间. Limit 使用 Interval 对象表示有界变化的值. 一般地,Interval[{xmin,xmax}] 表示在区间  到
到  中的某个不确定的值.
中的某个不确定的值.
Wolfram 语言对 Interval 对象可以进行算术运算:
Wolfram 语言以一个 Interval 对象来符号式地表示这个极限:
Limit[expr,x->x0] 求 expr 当 x 趋于 x0 时的极限. 当该值是无穷大时,求出 expr 在 x 等于 x0 时的留数常常是有用的. 留数由 expr 在 x0 处的幂级数展开式中的 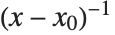 的系数给定.
的系数给定.
| Residue[expr,{x,x0}] | expr 在 x 等于 x0 时的留数 |
Padé 近似是一个有理函数,它可以被认为是对泰勒多项式的一个推广. 有理函数是多项式的比. 因为这些函数只使用基本的算术运算,它们很容易进行数值计算. 分母中的多项式使得能对具有有理奇点的函数进行近似.
| PadeApproximant[f,{x,x0,{n,m}}] | 给出 |
| PadeApproximant[f,{x,x0,n}] | 给出 |
更精确地说,解析函数 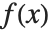 在一个常规点或极点
在一个常规点或极点 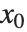 的
的 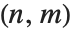 次 Padé 近似是有理函数
次 Padé 近似是有理函数 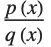 ,其中
,其中 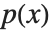 是一个
是一个 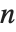 次多项式,
次多项式,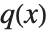 是一个
是一个 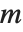 次多项式,
次多项式, 对
对 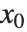 点的正式幂级数以
点的正式幂级数以 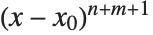 项开始. 如果
项开始. 如果 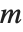 等于
等于 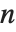 ,那么这个近似被称为
,那么这个近似被称为 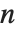 次对角 Padé 近似.
次对角 Padé 近似.
在 Wolfram 语言中 PadeApproximant 被推广使得能够对分支点展开.